
- •7. Диагональные и треугольные матрицы[править | править вики-текст]
- •Симметричные и кососимметричные матрицы[править | править вики-текст]
- •9. Минором к элементу определителя -го порядка называется определитель -го порядка, полученный из исходного вычеркиванием -той строки и -того столбца.
- •10. Сложение матриц и умножение на число
- •3) Находим матрицу алгебраических дополнений
- •Свойства фундаментальной системы решений[править | править вики-текст]
- •Формулы вычисления векторного произведения векторов
- •Свойства векторного произведения векторов
- •Свойства смешанного произведения векторов
- •Свойства[править | править вики-текст]
- •26. Составление канонических уравнений прямой в пространстве.
- •29. Формула для вычисления расстояния от точки до прямой в пространстве
- •Свойства бесконечно малых последовательностей[править | править вики-текст]
- •Свойства сходящихся последовательностей[править | править вики-текст]
- •Свойства[править | править вики-текст]
- •34. Предел функции по Гейне[править | править вики-текст]
- •Предел функции по Коши[править | править вики-текст]
- •Левый и правый пределы функции
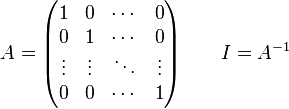
Линейная алгебра
1.Системой m линейных уравнений с n неизвестными называется система вида
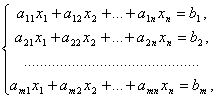
где aij и bi (i=1,…,m; b=1,…,n) – некоторые известные числа, а x1,…,xn – неизвестные. В обозначении коэффициентов aij первый индекс iобозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.
Коэффициенты
при неизвестных будем записывать в виде
матрицы 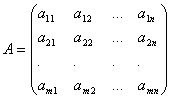 ,
которую назовём матрицей
системы.
,
которую назовём матрицей
системы.
Числа, стоящие в правых частях уравнений, b1,…,bm называются свободными членами.
Совокупность n чисел c1,…,cn называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c1,…,cn вместо соответствующих неизвестных x1,…,xn.
Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:
Система может иметь единственное решение.
Система может иметь бесконечное множество решений. Например,
 .
Решением этой системы является любая
пара чисел, отличающихся знаком.
.
Решением этой системы является любая
пара чисел, отличающихся знаком.И третий случай, когда система вообще не имеет решения. Например,
 ,
если бы решение существовало, то x1 +
x2 равнялось
бы одновременно нулю и единице.
,
если бы решение существовало, то x1 +
x2 равнялось
бы одновременно нулю и единице.
Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной. Если решение одно то система определённая, если система имеет бесконечное множество решений то она неопределённая.
2. Формулы Крамера и матричный метод решения систем линейных уравнений не имеют серьезного практического применения, так как связаны с громоздкими выкладками. Практически для решения систем линейных уравнений чаще всего применяется метод Гаусса, состоящий в последовательном исключении неизвестных по следующей схеме.Для того чтобы решить систему уравнений
 выписывают
расширенную матрицу этой системы
выписывают
расширенную матрицу этой системы  и
над строками этой матрицы производят
элементарные преобразования, приводя
ее к виду, когда ниже главной диагонали,
содержащей элементы
и
над строками этой матрицы производят
элементарные преобразования, приводя
ее к виду, когда ниже главной диагонали,
содержащей элементы ![]() будут
располагаться нули. Разрешается: 1)
изменять порядок строк матрицы, что
соответствует изменению порядка
уравнений; 2) умножать строки на любые
отличные от нуля числа, что соответствует
умножению соответствующих уравнений
на эти числа; 3) прибавлять к любой строке
матрицы другую, умноженную на отличное
от нуля число, что соответствует
прибавлению к одному уравнению системы
другого, умноженного на число. С помощью
этих преобразований каждый раз получается
расширенная матрица новой системы,
равносильной исходной, т. е. такой
системы, решение которой совпадает с
решением исходной системы.
будут
располагаться нули. Разрешается: 1)
изменять порядок строк матрицы, что
соответствует изменению порядка
уравнений; 2) умножать строки на любые
отличные от нуля числа, что соответствует
умножению соответствующих уравнений
на эти числа; 3) прибавлять к любой строке
матрицы другую, умноженную на отличное
от нуля число, что соответствует
прибавлению к одному уравнению системы
другого, умноженного на число. С помощью
этих преобразований каждый раз получается
расширенная матрица новой системы,
равносильной исходной, т. е. такой
системы, решение которой совпадает с
решением исходной системы.
Пусть
нам требуется решить систему из n линейных
алгебраических уравнений с nнеизвестными
переменными вида 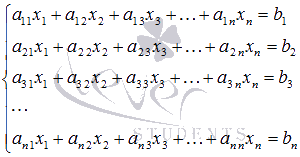 ,
и пусть определитель ее основной матрицы
отличен от нуля.
,
и пусть определитель ее основной матрицы
отличен от нуля.
Будем
считать, что ![]() ,
так как мы всегда можем этого добиться
перестановкой местами уравнений системы.
Исключим неизвестную переменную x1 из
всех уравнений системы, начиная со
второго. Для этого ко второму уравнению
системы прибавим первое, умноженное
на
,
так как мы всегда можем этого добиться
перестановкой местами уравнений системы.
Исключим неизвестную переменную x1 из
всех уравнений системы, начиная со
второго. Для этого ко второму уравнению
системы прибавим первое, умноженное
на ![]() ,
к третьему уравнению прибавим первое,
умноженное на
,
к третьему уравнению прибавим первое,
умноженное на ![]() ,
и так далее, к n-ому уравнению
прибавим первое, умноженное на
,
и так далее, к n-ому уравнению
прибавим первое, умноженное на ![]() .
Система уравнений после таких
преобразований примет вид
.
Система уравнений после таких
преобразований примет вид
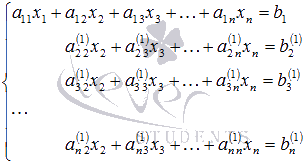 где
где 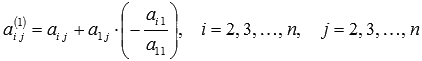 ,
а
,
а 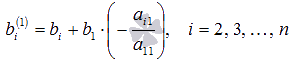 .
.
К такому же результату мы бы пришли, если бы выразили x1 через другие неизвестные переменные в первом уравнении системы и полученное выражение подставили во все остальные уравнения. Таким образом, переменная x1 исключена из всех уравнений, начиная со второго.
Далее
действуем аналогично, но лишь с частью
полученной системы, которая отмечена
на рисунке
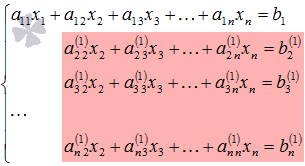
Будем
считать, что ![]() (в
противном случае мы переставим местами
вторую строку с k-ой,
где
(в
противном случае мы переставим местами
вторую строку с k-ой,
где ![]() ).
Приступаем к исключению неизвестной
переменной x2 из
всех уравнений, начиная с третьего.
).
Приступаем к исключению неизвестной
переменной x2 из
всех уравнений, начиная с третьего.
Для
этого к третьему уравнению системы
прибавим второе, умноженное на ![]() ,
к четвертому уравнению прибавим второе,
умноженное на
,
к четвертому уравнению прибавим второе,
умноженное на ![]() ,
и так далее, к n-ому уравнению
прибавим второе, умноженное на
,
и так далее, к n-ому уравнению
прибавим второе, умноженное на ![]() .
Система уравнений после таких
преобразований примет вид
.
Система уравнений после таких
преобразований примет вид
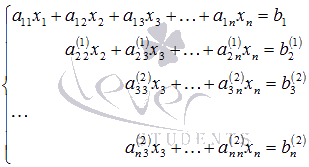 где
где 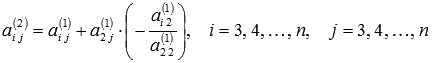 ,
а
,
а 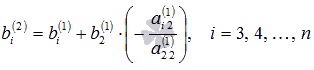 .
Таким образом, переменная x2 исключена
из всех уравнений, начиная с третьего.
.
Таким образом, переменная x2 исключена
из всех уравнений, начиная с третьего.
Далее
приступаем к исключению неизвестной x3,
при этом действуем аналогично с отмеченной
на рисунке частью системы
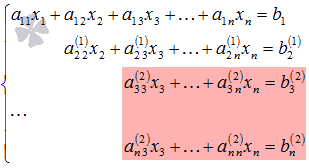
Так
продолжаем прямой ход метода Гаусса
пока система не примет вид
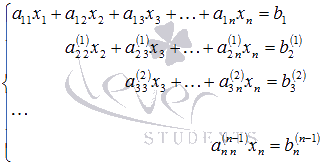
С
этого момента начинаем обратный ход
метода Гаусса: вычисляем xn из
последнего уравнения как 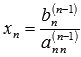 ,
с помощью полученного значения xn находим xn-1 из
предпоследнего уравнения, и так далее,
находим x1 из
первого уравнения.
,
с помощью полученного значения xn находим xn-1 из
предпоследнего уравнения, и так далее,
находим x1 из
первого уравнения.
3. Метод Гаусса — Жордана (метод полного исключения неизвестных) — метод, который используется для решения квадратных систем линейных алгебраических уравнений, нахождения обратной матрицы, нахождения координат вектора в заданном базисе или отыскания ранга матрицы. Метод является модификацией метода Гаусса. Назван в честь К. Ф. Гаусса и немецкого геодезиста и математика Вильгельма Йордана[1].
Пусть дано:
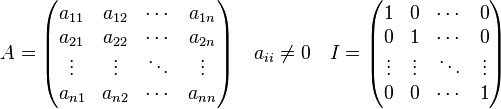
Прямой ход (алгоритм образования нулей под главной диагональю)[править | править вики-текст]
Разделим первую строку матрицы А на
 получим:
получим: 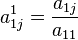 ,
j — столбец матрицы А.
,
j — столбец матрицы А.Повторяем действия для матрицы I, по формуле:
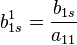 ,
s — столбец матрицы I
,
s — столбец матрицы I
Получим:
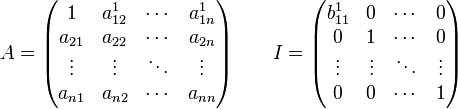
Будем образовывать 0 в первом столбце :
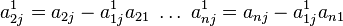
Повторяем действия для матрицы І, по формулам :
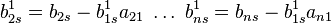
Получим:
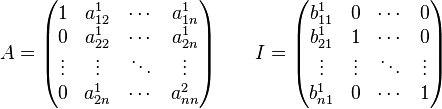
продолжаем выполнять аналогичные операции, используя формулы :
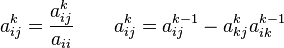
при
условии, что ![]()
Повторяем действия для матрицы І, по формулам :
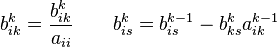
при
условии, что ![]()
Получим :
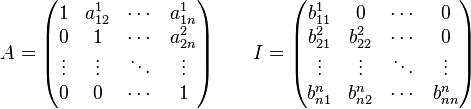
Обратный ход (алгоритм образования нулей над главной диагональю)[править | править вики-текст]
Используем
формулу: ![]() ,
при условии, что
,
при условии, что ![]()
Повторяем
действия для матрицы І, по формуле : ![]() ,
при условии, что
,
при условии, что ![]()
Окончательно получаем :
4.метод треугольников, студенческий метод, метод разложения по столбцу или строчке.
5. Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём
![]()
Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A11 элемента a11, 2-ое уравнение – на A21 и 3-е – на A31:
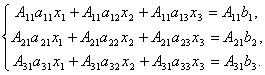
Сложим эти уравнения:
![]()
Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца
![]() .
.
Далее рассмотрим коэффициенты при x2:
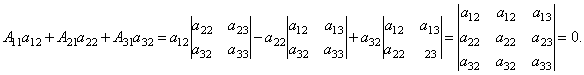
Аналогично можно
показать, что и
![]() .
.
Наконец несложно
заметить, что
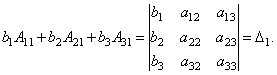
Таким образом,
получаем равенство:
![]() .
.
Следовательно,
![]() .
.
Аналогично
выводятся равенства
![]() и
и
![]() ,
откуда и следует утверждение теоремы.
,
откуда и следует утверждение теоремы.
Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.
. Рангом матрицы называется наибольший из порядков отличных от нуля ее миноров.
Теорема: Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.
RgA = RgA*.
Очевидно,
что система (1) может быть записана в
виде:
x1![]() +
x2
+
x2 ![]() +
… + xn
+
… + xn 
Доказательство.
1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А->А* не изменяют ранга.
2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.
6. Определителем матрицы А (определителем n-го порядка) называется алгебраическая сумма n! слагаемых, каждое из которых есть произведение n элементов матрицы, взятых по одному из каждой строки и каждого столбца. При этом произведение берётся со знаком «+», если подстановка из индексов входящих в него элементов чётная, и со знаком «» в противном случае.
10. При транспонировании определитель не меняется (напомним, что транспонирование матрицы и определителя означает перемену строк и столбцов местами).
20. Если все элементы строки (или столбца) определителя равны нулю, то определитель равен нулю.
30. Если все элементы какой-нибудь строки определителя имеют общий множитель, то его можно вынести за знак определителя.
40. Если две строки определителя поменять местами, то определитель сменит знак.
50. Если две строки определителя пропорциональны, то определитель равен нулю.
60. Если в определителе все элементы к-ой строки есть суммы двух слагаемых, то определитель равен сумме двух определителей, в которых все строки, кроме к-ой, такие же как и в данном определителе. На месте элементов к-ой строки одного из них стоят первые слагаемые элементов к-ой строки данного определителя, а на месте элементов к-ой строки второго – вторые их слагаемые.
70. Если к одной строке определителя прибавить другую его строку, все элементы которой умножены на одно и то же число, то определитель не изменится.
80. Дополнительный минор и алгебраическое дополнение не зависит от того, какой элемент стоит в к-ой строке и р-ом столбце определителя.
Теорема Лапласа
Пусть
выбраны любые ![]() строк
матрицы
строк
матрицы ![]() .
Тогда определитель матрицы
равен
сумме всевозможных произведений
миноров
-го
порядка, расположенных в этих строках,
на их алгебраические дополнения.
.
Тогда определитель матрицы
равен
сумме всевозможных произведений
миноров
-го
порядка, расположенных в этих строках,
на их алгебраические дополнения.
![]()
где
суммирование ведётся по всевозможным
номерам столбцов ![]()
7. Диагональные и треугольные матрицы[править | править вики-текст]
Если все элементы вне главной диагонали нулевые, A называется диагональной. Если все элементы над (под) главной диагональю нулевые, A называется нижней (верхней) треугольной матрицей.
Симметричные и кососимметричные матрицы[править | править вики-текст]
Квадратная матрица A, совпадающая со своей транспонированной, т.е., A = AT, называется симметричной. Если же, A равна минус транспонированной, т.е., A = −AT, A называется кососимметричной. В случае комплексных матриц симметрия часто заменяется понятием самосопряжённости, и в этом случае требуется, чтобы выполнялось A∗ = A, где звёздочка означает сопряжено-транспонированную матрицу, т.е транспонированную сопряжённой к A.
По спектральной теореме для вещественных симметричных матриц и комплексных Эрмитовых матриц существуют базисы, состоящие из собственных векторов. То есть, люой вектор пространства можно представить в виде линейной комбинациисобственных векторов. В обоих случаях все собственные значения вещественны.[1] Эту теорему можно распространить на бесконечномерный случай, когда матрицы имеют бесконечно много строк и столбцов.
8.
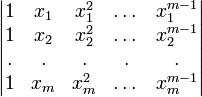
Вычтем
из последнего столбца предпоследний,
уможенный на ![]() ,
из
,
из ![]() -го
—
-го
— ![]() -й,
уможенный на
,
из
-й,
уможенный на
,
из ![]() -го
—
-го
— ![]() -й,
уможенный на
и
так далее для всех стобцов. Эти
преобразования не меняют определитель
матрицы. Получим
-й,
уможенный на
и
так далее для всех стобцов. Эти
преобразования не меняют определитель
матрицы. Получим
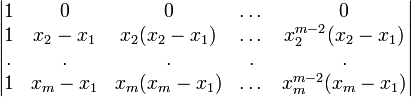
Раскладывая этот определитель по элементам первой строки, получаем, что он равен следующему определителю:
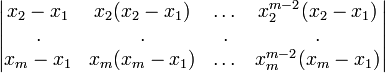
Для
всех
от
1 до ![]() вынесем
из
-й
строки множитель
вынесем
из
-й
строки множитель ![]() .
Получим
.
Получим
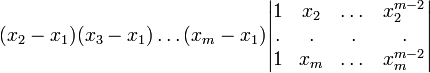
Подставим значение имеющегося в предыдущей формуле определителя, известного из индукционного предположения:
![]() ■
■
9. Минором к элементу определителя -го порядка называется определитель -го порядка, полученный из исходного вычеркиванием -той строки и -того столбца.
Алгебраическим
дополнением ![]() к
элементу
определителя
-го
порядка называется число
к
элементу
определителя
-го
порядка называется число![]()
10. Сложение матриц и умножение на число
Сложение
определено только для матриц одинаковых
размеров. Определение 14.2 Суммой
матриц ![]() и
и ![]() размеров
размеров ![]() является
матрица
является
матрица ![]() таких
же размеров, у которой
таких
же размеров, у которой ![]() ,
, ![]() ,
, ![]() .
.
Другими словами, при сложении матриц складываются элементы, стоящие на одинаковых местах. Например,
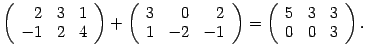 Определение 14.3 Произведением
матрицы
размеров
на
число
Определение 14.3 Произведением
матрицы
размеров
на
число ![]() называется
матрица
таких
же размеров, у которой
называется
матрица
таких
же размеров, у которой ![]() ,
,
.
,
,
.
Другими
словами, при умножении матрицы на число
все ее элементы умножаются на это число.
Например, 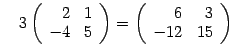 .
.
Легко проверить, что операции сложения матриц и умножения матрицы на число, называемые линейными операциями, обладают следующими свойствами:
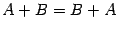 --
свойство коммутативности;
--
свойство коммутативности;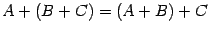 --
свойство ассоциативности;
--
свойство ассоциативности;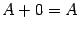 ;
;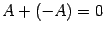 ;
;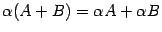 --
свойство дистрибутивности;
--
свойство дистрибутивности;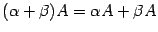 ;
;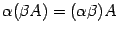 ;
;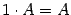 .
.
транспонирование матрицы - это операция над матрицей, когда ее строки становятся столбцами с теми же номеромами.
![]()
![]()
![]()
![]()
![]()
11.Чтобы
матрицу ![]() можно
было умножить на матрицу
можно
было умножить на матрицу ![]() нужно, чтобы
число столбцов матрицы
равнялось
числу строк матрицы
.
нужно, чтобы
число столбцов матрицы
равнялось
числу строк матрицы
.
12. 1) Сначала находим определитель матрицы.
2) Находим
матрицу миноров ![]() .
.
