
- •Критерий Коши равномерной сходимости
- •[Править]Признак Вейерштрасса
- •[Править]Признак Абеля-Дирихле
- •Предельная форма
- •Доказательство
- •Примеры
- •Доказательство
- •Признак сходимости д’Аламбера в предельной форме
- •Доказательство
- •Примеры
- •Доказательство.
- •Свойства
- •Производные
- •Доказательство
- •20. Непрерывность несобственного интеграла по параметру
- •21. Радиус сходимости степенного ряда. Формула Коши-Адамара
- •Радиус сходимости[править | править вики-текст]
- •22. Производная по направлению. Градиент. Экстремальное свойство градиента
- •24. Теорема Вейерштрасса о наибольшем и наименьшем значении
- •25. Степенные ряды. Первая теорема Абеля
- •Доказательство
- •26. Необходимое условие экстремума
- •27. Признак сравнения рядов в предельной форме
- •Доказательство
- •33. Разложение функций в степенной ряд. Ряд Тейлора
- •36. Повторные пределы. Теорема о повторных пределах (для функции двух переменных)
- •37. Аналитические свойства степенных рядов (непрерывность, интегрируемость, дифференцируемость) Теорема о равномерной сходимости и непрерывности степенного ряда
- •Описание метода
- •Д вумерный случай
Определение: |
Пусть
на
|
1. Равномерная сходимость функционального ряда. Непрерывность суммы ряда. Далее всё будем писать на языке функциональных рядов, так как их наиболее удобно использовать в математическом анализе, и вообще это очень круто и популярно.
Критерий Коши равномерной сходимости
Теорема (Критерий Коши равномерной сходимости): |
Ряд
равномерно сходится на
|
Доказательство: |
|
По
определению равномерной сходимости,
В
силу предыдущего неравенства,
По
условию критерия Коши, Как
и в первой половине доказательства, Значит, определение равномерной сходимости проверено. |
|
[Править]Признак Вейерштрасса
Существует простой признак для проверки равномерной сходимости (признак Вейерштрасса)
Можно
рассматривать ![]() и
при этом сохраняется терминология
числовых рядов, связанная с абсолютной
и условной сходимостью.
и
при этом сохраняется терминология
числовых рядов, связанная с абсолютной
и условной сходимостью.
Как и в рядах, абсолютная сходимость сильнее сходимости: из абсолютной сходимости вытекает сходимость.
Теорема (Вейерштрасс): |
, |
Доказательство: |
|
Применим критерий Коши:
Сопоставляя
с предыдущим неравенством, которое
верно
|
|
[Править]Признак Абеля-Дирихле
Теорема (Абель-Дирихле): |
Для
равномерной сходимости на
множестве
ряда
1)Частичные
суммы 2)Последовательность
функций |
Доказательство: |
|
Монотонность
последовательности
позволяет
при каждом
где Если
выполнена пара условий 1) и 2), то с одной
стороны существует такая
постоянная |
|
Теорема о непрерывности суммы функционального ряда.
Теорема.
Если все члены ряда ![]() (1)
- непрерывные на [a;b] ф-ции,
а ряд (1) сх-ся равномерно на [a;b], то
его сумма S(x) также
непрерывна на отрезке [a;b].
(1)
- непрерывные на [a;b] ф-ции,
а ряд (1) сх-ся равномерно на [a;b], то
его сумма S(x) также
непрерывна на отрезке [a;b].
Док-во:
Пусть ![]() -
произв.точка [a;b]. Для
опр-ности будем считать, что
-
произв.точка [a;b]. Для
опр-ности будем считать, что ![]() (a;b). Нужно
док-ть, что S(x)=
непрерывна
в
,
т.е
(a;b). Нужно
док-ть, что S(x)=
непрерывна
в
,
т.е ![]()
![]()
![]()
![]() <
<![]() (2),
(2), ![]() [a;b]. По
усл-ю, ряд (1) равномерно сх-ся
на [a;b], т.е
[a;b]. По
усл-ю, ряд (1) равномерно сх-ся
на [a;b], т.е ![]()
![]() n
n![]()
![]() [a;b]
[a;b]
![]() <
<![]() (3), где
(3), где ![]() =
=![]() .Фиксируем
номер
.Фиксируем
номер ![]() ,
тогда при n=
,
тогда при n=![]() из
(3) получаем:
из
(3) получаем: ![]() <
(4). В
частности, при x=
находим
<
(4). В
частности, при x=
находим ![]() <
(5). Ф-ция
<
(5). Ф-ция ![]() (x) непрерывна
в
как
сумма конечного числа непрерывных
ф-ций. По опр-ю непрерывности
(x) непрерывна
в
как
сумма конечного числа непрерывных
ф-ций. По опр-ю непрерывности
![]() [a;b]
[a;b]
![]() <
(6). Восп.
рав-вом S(x)-S(
)=(S(x)-
(x))+(
(x)-
(
))+(
(
)-S(
)). Отсюда
получаем, исп. (4)-(6) и нер-во треугольника
:
<
, для
[a;b], т.е
справедливо утв-е (2). В силу произвольности
точки
ф-ция S(x) непрерывна
на отрезке [a;b].
<
(6). Восп.
рав-вом S(x)-S(
)=(S(x)-
(x))+(
(x)-
(
))+(
(
)-S(
)). Отсюда
получаем, исп. (4)-(6) и нер-во треугольника
:
<
, для
[a;b], т.е
справедливо утв-е (2). В силу произвольности
точки
ф-ция S(x) непрерывна
на отрезке [a;b].
2. Радикальный признак Коши (сходимости числового ряда):
-
Если для числового ряда
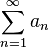
с неотрицательными членами существует такое число
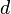 ,
, 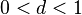 ,
что, начиная с некоторого номера,
выполняется неравенство
,
что, начиная с некоторого номера,
выполняется неравенство 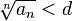 ,
то данный ряд сходится.
,
то данный ряд сходится.
