10.Үлкен сандар заңы.Орталық шектік теорема.
Ықтималдықтар теориясында үлкен сандар заңы деп кездейсоқ шамалардың арифметикалық ортасына қатысты теорияларды д.а.
Орталық
шектер теорема. Тәуелсіз Ԑ1
Ԑ2
Ԑn
кездейсоқ шамаларының математикалық
үміттері мен дисперсияларын бар деп
алып белгілеулер еңгізейіk
және
;
Бір
шарттар тобы орын-да
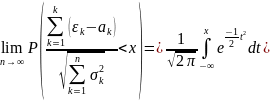бола,
онда
Ԑ1,Ԑ2,...,Ԑn тізбегі үшін орталық шектік теорема орындалады д.а. О.Ш.Т-ң мазмұны мынау: Тұрмыста көптеп кездесетін Ԑ1+Ԑ2+...+Ԑn қосындысын нормалағаннан кейін, оның үлестірімдік функциясы қалыпты үлестірім заңы болып табылады. Муавр-Лапластың интергалдық шектік теориясы жоғарыдағы бірдей үлестірімі бар кездейсоқ шамалар үшін дәлелденген теореның жекеше бір жағдайы n рет жүргізілген Бернули тәжірибесинен A оқиғасының n саны V бойынша онда V= Ԑ1+Ԑ2+... +Ԑn деп жазуға болады, мұндағы Ԑn (k=1,2,..n) кездейсоқ шамаларының үлестірім бірдей
Ԑn
=
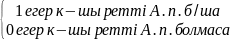
Олай
болса
a<=b
сандары
үшін n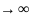
болғанда
P(a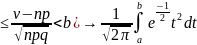
Ляпунов теориясы. Егер тәуелсіз
,
кездейсоқ шамаларының үшінші ретті
абсолютті моменттер бар болса және
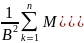орындалса,
онда x
б/ша бірқалыпты
шектік
қатынасы орындалады.
11.Мат статистика(таңдама,-көлемі,варианта,стат-қ қатар,дисперсия)
N
бақылау нәтижесі кездейсоқ шама мәндері
дейміз. Х КШ-ң мүмкін мәндерінің жиынтығы
мат статискада бас жиынтық д.а. Х КШ-ң
ықтималдықтыңтың үл-м заңы Х бас
жиынтығының үл-м заңы болып саналады.
Х КШ-ң үл-м шамасының тәуелсіз
КШ-р
жиынтығы Х бас жиынтығының кездейсоқ
таңдамасы д.а. Бас жиынтық көлемі:
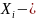таңдама
элементтері. Кездейсоқ таңдама эл-ң
Х1,Х2...Хn мүмкін мәндерін тандама д.а.
Мұнда
варианта.
Сәйкесінше Х1,Хn-ең кіші ж/е ең үлкен
варианталар д.а. Олардың айырымы таңдама
құлашы
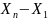X КШ-ң дискретті н/се үздіксіз болуына
байланысты статистикалық модель
сәйкесінше дискретті н/се үздіксіз
д.а. Таңдама {
}
вариациялық қатар н/се статистикалық
қатар түрінде түзіледі
Вариациялық
қатар эл-рі (варианталар) қатарда өсуіне
қарай н/се кемуіне қарай орналастырылады.
Егер
эл-ті вариациялық қатарда
кездесетін
болса, онда ол таңдама жиілігі д.а.
Олардың қосындысы таңдама көлемңн
береді. N=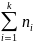
k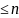
Таңдамадағы мәндерді 1-ші жолға, ал
олардың жиіліктерін 2-ші жолға орн кесте
құрсақ,(
қос сандарының (шекті) тізбегі таңдаманың
статистикалық
қатары д.а.
Таңдаманың салыстырмалы жиілігі
Егер таңдаманың көлемі үлкен болса,
онда оның эл-н, топтарға біріктіріп,
тәжірибе нәтижелерінен топтастырылған
статистикалық қатар құрамыз. Ол үшін
таңдаманың барлық эл-рі орн интервалдарды
өзара айқаспайтын к жеке интервалдарға
бөлеміз. Интервалдар саны:
мұнда
n-таңдама
көлемі.
12.сенім
интервалы.Қалыпты үл-ді КШ-ң
белгіліде мат күтім-ң бағамы....
Қалыпты үлестірімді бас жиынтықтың
параметрлері үшін сенім интервалы.
N(a;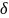
)
заңы б/ша қалыпты үлестірім бас жиынтық
сенім интервалы
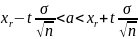мұнда t=
баған дәлдігі. Ал t мәні Лаплас ф-ң
Ф(t)=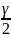
теңдігі
б/ша кесте арқылы табылады. Қалыпты
үлестірім-ң ықтималдық тығыздығы f(x)=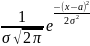
ф-я-ғы
-ны
белгілі деп алып,
сенімділігімен a үшін
,
,…,
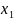таңдама б/ша сенімділік интервалын
ісдестіреміз таңдаманың ортасы x=
+
+…
қалыпты үлестірімді болаттындығын,
M(x)=a мен D(x)=
теңдіктері орындалатындығы бұрын
дәлелденді. Кездейсоқ шаманың интервалға
тиітсті болу ықтималдығы б/ша P(|x-a|<
)=
P(a-
<x<a+
)=2Ф(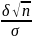
)
мұндағы t=
енді P(|x-a|<
)=
теңсіздігі орындалсын делік. Сонда
2Ф(t)=
қосымшалардағы Ф(x)=
ф-яның кестесін пайдаланып, Ф(x)=
теңдеуінен t=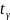
мәнін
табамыз Демек
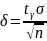ақырында P
=
Мағынасы
сенімділігі (
)
сенімділік интервалын белгісіз a
параметрін табады, ал бағалау дәлдігі
=
болады.