7.Таңдама.Үл-ң эмпирикалық ф-сы, полигон және гистограмма анық-ры

Х КШ-ң үл. шамасының тәуелсіз КШ-р жиынтығы Х бас жиынтығының кездейсоқ таңдамасы д.а.

Үл-ң эмпирикалық(таңдамалы) ф-сы F(x) қордаланған салыстырмалы жиіліктерінің мәндері арқ анық

Эмпирикалық ф-я графигі КШ-ң үлестірілім ф-я графигіне ұқсас

Төбелері нүктесінде орналасқан сынық сызық топтастырылған таңдама жиіліктері полигоны д.а.

Жеке интервалдарға табаны ретінде тұрғызылған тік4бұрыштан құралған, баспалдақ пішіндес фигура топтастырылған таңдама жиіліктерінің гистограммасы д.а. Бүкіл гистограмма ауданы таңдама көлемі n-ге тең.

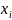
	1	2	3	4
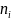
	3	1	4	2

8.Ықтималдылықтар теориясының шектік теоремасы.Чебышев теңсіздігі

Көптеп кездесетін кездейсоқ шамалардың саны ақырсыздыққа ұшталғанда, үл. заңының шектік жағдайын қарастырудың практикада үлкен маңызы бар. Муавр-Лапластың төңіректік және интегралдық теоремалары-шектік теоремалардың алғашқылары болды. Шектік теоремалардың алғашқылары өрісі өте кең, бірақ біз оларды 2 бағытта қарастырамыз: үлкен сандар заңы ж/е орталық шектік теорема. Үлкен сандар заңы деп—кездейсоқ шамалардың арифметикалық ортасына қатысты теоремаларды айтады. Орталық шектік теорема – тәуелсіз кездейсоқ шамаларының математикалық үміттері мен дисперсияларын бар деп алып, белгілеулер енгізейік: 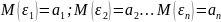және ; белгілі шарттар тобы орындалса болса, онда тізбегі үшін орталық шектік теорема орындалады деп атайды.

9.Вариациялық қатар сип-ры. Үл-ң белгісіз параметрлері(таңдама орт,дисп)

Х кездейсоқ шамасының мүмкін болатын барлық мәндерін Бас жиын деп, n рет тәжірибе жүргізгенде n б-ған Х шамасының х_1, х₂, х_n мәндерін статистикалық қатар деп атайды. Қатар элем-н өсу тәртібі ббойынша орналастырылғаннан кейін шыққан x₍₁₎ x₍₂₎ x_{(n) )}1.2) қатарын варияциялық қатар деп, ал онын элементтерін варианттар д.а. Әрбір практикалық өлшеулерге сәйкес (1.2) варияциялық ққатары табылады. Варианттардың орналасуы мынандай алдымен х₍₁₎= min(x_1..x_n) келесі x₍₂₎=min (х_2…x_n), ақырында х_(n)= max(x₂…x_n) Мәндері табылады, сонда (1.2) қатары шығады. Варияциялық қатары грфик түрінде кескіндеудің екі жолы бар: Палигон салу және гистограмма салу. Варияциялық қатардағы әр түрлі варианттары кестенің 1 жолына орналастырады. Кестенің 2 жолына v_i=n_i/ n жиіліктері жазылады, мұндағы к_i i-ші варианттың қанша рет қайталағанын көрсетеді. Мысал. қайсібір кездейсоқ шаманы зерттеу үшін 40 рет тәуелсіз тәжірибе жүргізгенде мынадай сандар n.б :

10 13 10 9 9 12 12 6 7 9

8 9 9 11 14 13 9 8 8 7

10 10 11 11 12 12 8 7 9 10

14 13 8 8 9 10 11 11 11 12

Варианттарды іріктеп,өсу тәртібімен орналастырайық: 6 7 8 9 10 11 12 13 14 Бұл қатардағы варианттардың әрқайсы қанша рет кездесетінің санап алсақ,оларға сәйкес жиіліктері шығады: 1 3 6 8 6 6 5 3 және 2. Енд қатардың әрбір элементіне v=1/40 жиілігін сәйкес келтіріп, мынандай кесте құрамыз

xi	6	7	8	9	10	11	12	13	14
vi	1/40	3/40	6/40	8/40	6/40	6/40	5/40	3/40	2/40

1 кесте бойынша график салсақ, полигон деп аталады.фигура шығады.

Статистикалық қатардың көлемі үлкен болған жағдайда кездейсоқ шаманың мәндерінің ұзындықтары бірдей болатын интервалдарға бөледі. Бұл операциялық варияциялық қатардың элементтеріін топтастыру деп аталады. Кездейсоқ шаманың мәндерін топтастырғанда, әрбір элемент бірғана интервалда табуы міндетті. Ал, интервалдың санын тағайындау мәселесін экспериментатордың өзі, мақсатына орай шешеді. Әдетте интервалдар санын 15 тен асырмайды. Әрі қарай әр инервалға кіретін таңдама мәндерін санап, жиіліктерді есептейді. Ақырында табандары- интервадар болатын және жиіліктері-жиілік болатын тік төртбұрыштар салады. Оны гистограмма деп атайды.

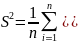Таңдама орташасы деп тендігімен анықталған Х кездейсоқ шамасын айтады. Таңдама дисперсиясы деп Теңлдігімен анықталған S² кездейсоқ шамасын айтады.