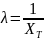1.Бірқалыпты үлестірілім

Егер КШ-сы қабылдайтын мәндер (a,b) аралығына тиісті болса ж/е f(x) үл. тығыздығы (a,b) аралығының ұзындығына пропорционал болса, онда КШ-ң бірқалыпты үлестірімі бар д.а. Сөйтіп:

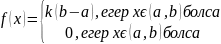
К-пропорционалдық коэффициент. ал біздің жағдайда демек f Сонда бірқалыпты үл. ф-сы: КШ-ң бірқалыпты үл. ф-я сандық сипаттамалары: ; ;

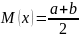Бірқалыпты үлес-ді КШ-ң мәндерінің берілген [c,d] аймағындағы аралық ұзындығына тең. P(c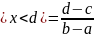

Үлес-м ф-сы мен үл. тығыздығының графиктері

2. Көрсеткіштік үлестірілім

Үл. тығыздығы түріндеанықталған КШ көрсеткіштік үл-ді д.а. Мұнда 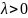, оның үл. ф-сы 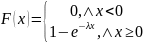КҮКШ-ң мәндерінің аралықта жату (a,b) аралығында жату ықтималдығы P(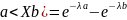 . Оның мат. күтімі

КҮКШ-ң мат. күтімі л параметрінің кері шамасыеа тең.Жалпы дисперсиялық ф-сын табу формуласы негізінде көрсеткіштік үлестірімді бұдан 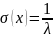яғни КҮКШ-ң мат-қ күтімімен ортақ логранттық ауытқуымен өзара тең.

КҮКШ тек оң шамаларды қабылдайды.Бұл үлестірімнің мысалы ретінде радиоактивті элементтердің ыдырау уақытын алуға болады.Оның орташа ыдырау уақыты Ал оның жартылай ыдырау уақыты медиана

3.Қалыпты үлестірім

N(a,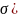 Үлестірім тығыздығы анықталатын КШ қалыпты үл. д.а. Үл. тығ-ң графигі Гаусс қисығы д.а. Ол бүкіл сандық осьте анықталған

Қалыпты үл-ді КШ мәндерінің белгілі бір аралыққа түсу ық-ң фор-н Лаплас ф-н қолданып 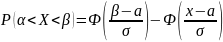табылады.Демек, 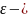дің қалыпты үл. ф-сы фор-н анықталады. Егер және болса, онда функ-н стандартты қалыпты үл-ң ықтималдылық тығыздығы деп, ал функ-н стандарт қалыпты үл-м функ-ы д.а.

4.Үлестірілім ф-сы.( ) аралыққа түсу ықтималдығы. Р-ретті квантиль.

Қалыпты үл-ді КШ-ң мәндерінің белгілі бір аралыққа түсу ық-ң фор-на Лаплас функ-н қолданып Лаплас функ-ы тақ. Математикалық күтім орта кв. ауытқу болғанда, яғни КШ N(0, заңымен үлестірілген болса, онда ол стандартты қалыпты үл-ді КШ болып саналады.

Х үзіліссіз КШ-ң үл-ң Р-ретті квантилі шарртарын қанағаттандыратын санын айтамыз.

5.Екі өлшемді кшү функ-ы. Үл. Тығыздығы

Бірдей ықтималдықтар кеңістігінде берілген кездейсоқ Х1(w1)...Xn(wn) шамалар жиынтығы көп өлшемді КШ д.а. n=1 КШ-бір өлшем, n=2 КШ –екі өлшемді (X,Y) түрінде жазылады. Екі өлшемді КШ-ны F(x,y) үл. ф-сы деп әрбір x,y сандар жұбы үшін X,Y шамалары сәйкесінше x,y мәндерінен кіші мән қабылдау ықтималдығы ф-сын айтамыз.

Екі өлшемді КШ үл. тығыздығы деп, үл. ф-ң екінші ретті аралас туындысын айтамыз.

КШ-ң үл. тығыздығы деп аталады.

6.Үл. Параметрінің нүктелік және интервалдық бағамдары.

Интервалдық бағамдар: Қалыпты үл. бас жиынтықтың параметрлері үшін сенім интервалы: N(a, заңы б-ша қалыпты үл. бас жиынтықтың сенім интервалы мұнда бағам дәлдігі. Ал t мәні Лаплас ф-ң 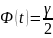теңдігі б-ша кесте арқ. табылады. Ал белгісіз параметрі үшін сенім интервалы 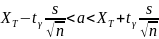мұнда s-түзетілген таңдаманың орташа кв. ауытқуы.

Нүктелік бағамдар: Параметрді нүктелік бағамдау әдістері

Бас жиынтық үлестірім параматрлерінің бағандарын табудын, мейлінше шынайлық және моменттеу әдісі.

Шынайлық әдісі

Бас жиынтықтын …, параметрлерінің бағандарын табу үшін λ{Xi} нақты тандама Xi алынды.Айнымылылардың нақты мәндері үшін, тандаманың үлестірім заңы.Шынайлық функциясы деп аталатын тек белгісіз параметрге тәуелді λ функциясымен өрнектеледі.Белгісіз параметрлердің бағамдары ретінде шынайлық функциясы максимум =L(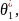 …, ) ие болатын мейлінше шынайлық бағалдары 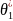,…, мәндері қабылданыды. Х дискретті КШ-ң үлестірілімің параметрлері бағамдалатын болып табылады.Ал тандаманың үлестірім заңы Р(X=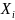 )= …, түрінде өрнектелетін болса, онда шынайлық функциясы тандыма элементтерінің бір мезгілде …, 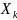мәндерін қабылдау ықтималдығына тең.

L( …, )= Р(X= )…P(W= ) үлестірілім тығыздығы P(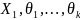 ) болатын үздіксіз Х кездейсоқ шамасының үл. параметрінің бағамдарын табу үшін, шынайылық ф-сы …, P( … ( )

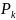Пуассон заңы бойынша үлестірімді бос жиынтықтың матиматикалық күтімінің, мейлінше шынайлық бағаны ретінде тандама бағамы ретінде тандама орташасы қабылданады. Бас орташасы белгілі қалыпты үлестірімді бас жиынтықтың дисперциясының мейлінше шынайлық бағаны ретінде тандама дисперциясы алынады.

Моменттер әдісі: бас жиынтық үлестірімнің к параметрі бар болса, оларды таңдама бойынша бағамдау үшін таңдамалық момент алынады. Нәтижелері бас жиынтық үлестірімінің сәйкес моменттерімен теңестіріледі. 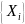таңдамасы бойынша көрсеткіштік үл-ң 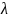параметрін табуда, бірінші ретті бастапқы момент матем-қ күтім болғандықтан таңдамалы ж/е бас орташалар теңестіріледі. F көрсеткіштік үлестірім үшін 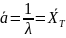сонымен ізделінді уақыт