
- •Основные неопределенности пределов и их раскрытие.
- •Односторонние пределы
- •Левый и правый пределы функции
- •Односторонние границы
- •Бесконечно малая и бесконечно большая
- •Бесконечно малая[править | править вики-текст]
- •Бесконечно большая[править | править вики-текст]
- •Свойства бесконечно малых[править | править вики-текст]
- •Непрерывность функции. Точки разрыва. Как исследовать функцию на непрерывность?
- •Непрерывность функции. Точки разрыва и их классификация Понятие непрерывности функции
- •Непрерывность функции в точке и на интервале
- •Точки разрыва функции и их классификация Определение точки разрыва
- •Точка разрыва первого рода
- •Точка разрыва второго рода
- •Точка устранимого разрыва
- •Примеры решения задач
Пределы функции в точке и на бесконечности
Пусть функция y =f(x) определена в некоторойокрестностиx0,кроме, может быть, самой точки x0.
Определение.ЧислоA называется пределом функцииy =f(x) в точке x0 (или при х →x0), если для любого сколь угодно малого числа ε> 0найдетсятакоечисло δ> 0, что для всех х ¹x0, удовлетворяющих неравенству
│ х –x0│< δ, выполняется неравенство│f(x) –А│<ε.
Или кратко:
![]() ε>
0
ε>
0 ![]() δ >
0,
x:│ х
–x0│<
δ, х
¹x0=>
│f(x)
–А│<ε.
δ >
0,
x:│ х
–x0│<
δ, х
¹x0=>
│f(x)
–А│<ε.
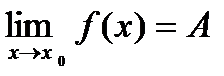
Г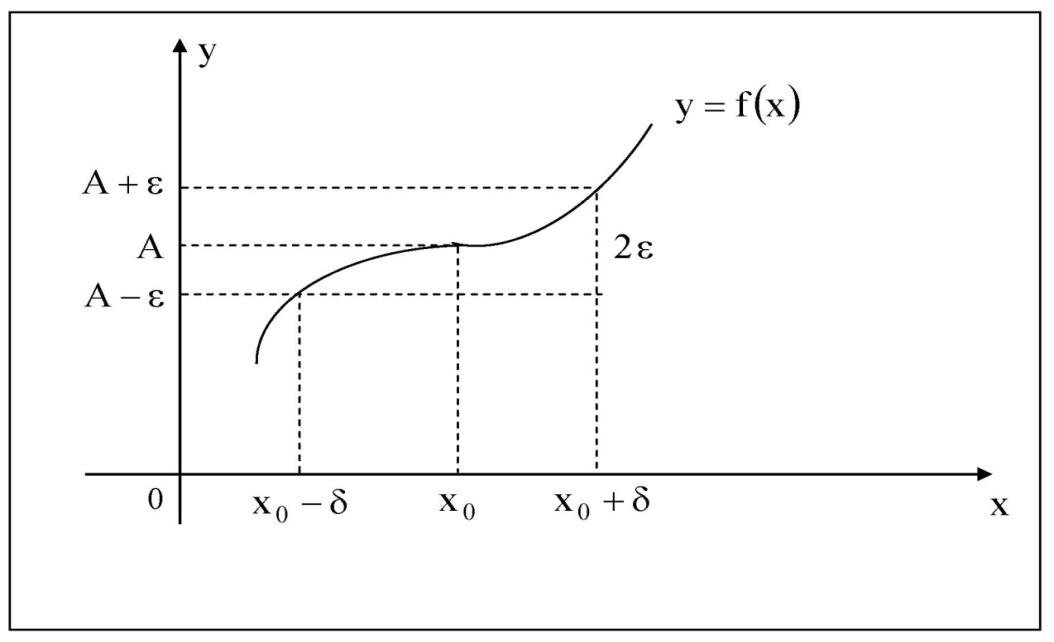 еометрический
смысл предела
функции заключается в следующем:
число
еометрический
смысл предела
функции заключается в следующем:
число 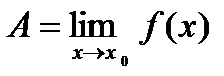 ,
если для любой ε – окрестности
точкиAнайдется
такая δ – окрестность точки x0,
что для всех х
¹x0 из
этой окрестности соответствующие
значения функции f(x)
лежат в ε – окрестности точки А.
,
если для любой ε – окрестности
точкиAнайдется
такая δ – окрестность точки x0,
что для всех х
¹x0 из
этой окрестности соответствующие
значения функции f(x)
лежат в ε – окрестности точки А.
Рис. 1
Пример:Доказать,
что
![]()
Решение. Возьмем
произвольное ![]() и
найдем
и
найдем ![]() такое,
что для всех x,
удовлетворяющих неравенству,
такое,
что для всех x,
удовлетворяющих неравенству, ![]() ,
выполняется неравенство
,
выполняется неравенство ![]() ,
то есть
,
то есть ![]() .
.
Взяв ![]() ,
видим, что для всех x,
удовлетворяющих неравенству,
,
видим, что для всех x,
удовлетворяющих неравенству, ![]() ,
выполняется неравенство
,
следовательно,
,
выполняется неравенство
,
следовательно,
![]()
Пусть
функция y
=f(x)
определена в промежутке (– ![]() ;
+
).
;
+
).
Определение.ЧислоA называется пределом
функцииf(x)
при х ![]() ,
если для любого числа ε >
0существуеттакоечисло M
= M (ε) >
0, что для всех значений x,
удовлетворяющих неравенству
│x│>M,выполняется
неравенство │f(x)
– А│< ε. В
этом случае пишут
,
если для любого числа ε >
0существуеттакоечисло M
= M (ε) >
0, что для всех значений x,
удовлетворяющих неравенству
│x│>M,выполняется
неравенство │f(x)
– А│< ε. В
этом случае пишут 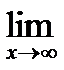 f(x)
= А.
f(x)
= А.
Или кратко:
ε> 0 M> 0, │x│ >M=> │f(x) –А│<ε.
f(x) = А.
Бесконечные пределы в конечной точке
Проколотой
окрестностью точки ![]() называется:
называется:
![]()
Пусть
функция ![]() определена
в некоторой проколотой окрестности
точки
определена
в некоторой проколотой окрестности
точки ![]() Говорят,
что
имеет бесконечный предел в
этой точке
Говорят,
что
имеет бесконечный предел в
этой точке ![]() если:
если:
![]()
В
этом случае функцию называют бесконечно
большой при ![]() Данный
общий случай можно разделить на два
частных:
Данный
общий случай можно разделить на два
частных:
и, соответственно
Пример 1
Дана
функция ![]()
 Найти
предел при
Найти
предел при ![]()
РЕШЕНИЕ |
СКРЫТЬ |
Функция
определена на всей вещественной оси
кроме т. |
|
|
|
|
|
Пределы на бесконечности
Число ![]() называют пределом
функции
на
бесконечности
называют пределом
функции
на
бесконечности ![]() если
если
![]()
Отсюда,
очевидно, следуют определения предела
на ![]()
и
на ![]()
Абсолютно аналогично определяется бесконечный предел на бесконечности:
Пример 2
Рассмотрим
функцию ![]()
РЕШЕНИЕ |
СКРЫТЬ |
При |
|
|
|
Свойства пределов функции
1° Предел суммы/разности двух функций равен сумме/разности их пределов:
![]()
Пример
Задание. Вычислить
предел ![]()
Решение. Воспользуемся первым свойство, разложим функцию на несколько более простых и отдельно найдем их пределы.
![]()
Ответ. ![]()
2° Предел произведения двух функций равен произведению их пределов:
![]()
Пример
Задание. Вычислить
предел ![]()
Решение. Воспользуемся вторым свойство, разложим функцию на несколько более простых и отдельно найдем их пределы.
![]()
![]()
Ответ. ![]()
3° Предел частного двух функций равен частному их пределов, при условии, что предел знаменателя не равен нулю:
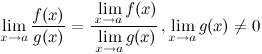
Пример
Задание. Вычислить
предел ![]()
Решение. Воспользуемся третьим свойство, сделаем числитель и знаменатель функции отдельными пределами и независимо найдем их.
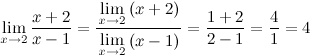
Ответ. ![]()
4° Константу можно выносить за знак предела:
![]()
Пример
Задание. Вычислить
предел ![]()
Решение. Воспользуемся первым и четвертым свойствами, разложим функцию на несколько более простых и отдельно найдем их пределы.
![]()
![]()
Ответ. ![]()
5° Предел степени с натуральным показателем равен степени предела:
![]()
Пример
Задание. Вычислить
предел ![]()
Решение. Воспользуемся пятым свойством, внесем предел под третью степень. Сначаланайдем предел более простой функции, а затем возведем его в третью степень.
![]()
Ответ. ![]()
1. Арифметические свойства предела функции. Пусть функции f и g определены на интервале ( a, b ), кроме быть может точки x0. Если существует пределы
![]() и
и ![]() ,
,
то существуют пределы в левых частях равенств и имеют место эти равенства :
a. ![]() б.
б. ![]()

Эти свойства вытекают из определения Гейне предела функции и соответствующих свойств сходящихся последовательностей. 2. Если
![]() ,
,
то
существует проколатая окрестность ![]() точки
точки ![]() ,
где функция f ( x ) ограничена.
Действительно,
если взять
,
где функция f ( x ) ограничена.
Действительно,
если взять ![]() =
1
=
1 ![]() 0 ,
то из существования конечного предела
следует, что существует
0 ,
то из существования конечного предела
следует, что существует ![]() 0,
что для всех x :
0
0,
что для всех x :
0 ![]() | x - x0 |
,
выполняется | f ( x )
- A |
1,
отсюда, | f ( x )
| - | A |
| x - x0 |
,
выполняется | f ( x )
- A |
1,
отсюда, | f ( x )
| - | A | ![]() | f( x )
- A |
1 ,
т.е.
| f( x )
- A |
1 ,
т.е.
![]()
3. Если
,
то
существует проколотая окрестность
точки
,
что для всех x ![]() :
:
![]()
Действительно, возьмем 0, тогда из существования конечного предела, следует, что существует окрестность , что для всех x :
![]()
4. Свойства, связанные с неравенствами. Если
, ![]()
и
для всех x
: f ( x ) ![]() g ( x )
, то A
B
Если
g ( x )
, то A
B
Если
= = A
и
для всех x
: ![]() , то
существует
, то
существует
![]()
Доказательства этих свойств следуют из следующих свойств для сходящихся последовательностей и определения предела функции по Гейне.
Основные неопределенности пределов и их раскрытие.
С непосредственным вычислением пределов основных элементарных функций разобрались.
При переходе к функциям более сложного вида мы обязательно столкнемся с появлением выражений, значение которых не определено. Такие выражения называютнеопределенностями.
Перечислим
все основные
виды неопределенностей:
ноль делить на ноль ![]() (0
на 0),
бесконечность делить на бесконечность
(0
на 0),
бесконечность делить на бесконечность ![]() ,
ноль умножить на бесконечность
,
ноль умножить на бесконечность ![]() ,
бесконечность минус бесконечность
,
бесконечность минус бесконечность ![]() ,
единица в степени бесконечность
,
единица в степени бесконечность ![]() ,
ноль в степени ноль
,
ноль в степени ноль ![]() ,
бесконечность в степени ноль
,
бесконечность в степени ноль ![]() .
.
ВСЕ ДРУГИЕ ВЫРАЖЕНИЯ НЕОПРЕДЕЛЕННОСТЯМИ НЕ ЯВЛЯЮТСЯ И ПРИНИМАЮТ ВПОЛНЕ КОНКРЕТНОЕ КОНЕЧНОЕ ИЛИ БЕСКОНЕЧНОЕ ЗНАЧЕНИЕ.
Раскрывать неопределенности позволяет:
упрощение вида функции (преобразование выражения с использованием формул сокращенного умножения, тригонометрических формул, домножением на сопряженные выражения с последующим сокращением и т.п.);
использование замечательных пределов;
применение правила Лопиталя;
использование замены бесконечно малого выражения ему эквивалентным(использование таблицы эквивалентных бесконечно малых).
Сгруппируем неопределенности в таблицу неопределенностей. Каждому виду неопределенности поставим в соответствие метод ее раскрытия (метод нахождения предела).
Эта таблица вместе с таблицей пределов основных элементарных функций будут Вашими главными инструментами при нахождении любых пределов.

Приведем парочку примеров, когда все сразу получается после подстановки значения и неопределенности не возникают.
Пример.
Вычислить
предел 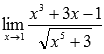
Решение.
Подставляем
значение:
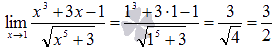
И сразу получили ответ.
Ответ:
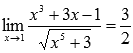
Пример.
Вычислить
предел ![]()
Решение.
Подставляем
значение х=0 в
основание нашей показательно степенной
функции:
![]()
То
есть, предел можно переписать в виде
![]()
Теперь займемся показателем.
Это есть степенная функция ![]() .
Обратимся ктаблице
пределов для
степенных функций с отрицательным
показателем. Оттуда имеем
.
Обратимся ктаблице
пределов для
степенных функций с отрицательным
показателем. Оттуда имеем ![]() и
и ![]() ,
следовательно, можно записать
,
следовательно, можно записать ![]() .
.
Исходя
из этого, наш предел запишется в виде:
![]()
Вновь
обращаемся к таблице пределов, но уже
для показательных функций с основанием
большим единицы, откуда имеем:
![]()
Ответ:
![]()
Разберем на примерах с подробными решениями раскрытие неопределенностей преобразованием выражений.
Очень часто выражение под знаком предела нужно немного преобразовать, чтобы избавиться от неопределенностей.
Пример.
Вычислить
предел 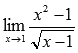
Решение.
Подставляем
значение:
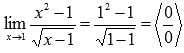
Пришли
к неопределенности. Смотрим в таблицу
неопределенностей для выбора метода
решения. Пробуем упростить выражение.
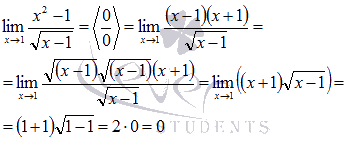
После преобразования неопределенность раскрылась.
Ответ:
![]()
Пример.
Вычислить
предел ![]()
Решение.
Подставляем
значение:
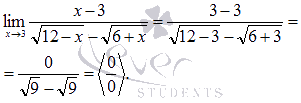
Пришли к неопределенности (0 на 0). Смотрим в таблицу неопределенностей для выбора метода решения и пробуем упростить выражение. Домножим и числитель и знаменатель на выражение, сопряженное знаменателю.
Для
знаменателя сопряженным выражением
будет ![]()
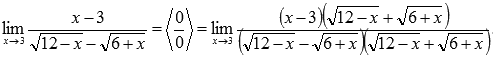
Знаменатель
мы домножали для того, чтобы можно было
применить формулу сокращенного умножения
– разность квадратов и затем сократить
полученное выражение.
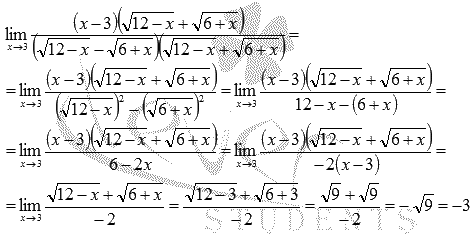
После ряда преобразований неопределенность исчезла.
Ответ:
![]()
ЗАМЕЧАНИЕ: для пределов подобного вида способ домножения на сопряженные выражения является типичным, так что смело пользуйтесь.
Пример.
Вычислить
предел 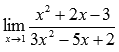
Решение.
Подставляем
значение:
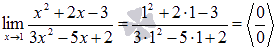
Пришли к неопределенности. Смотрим в таблицу неопределенностей для выбора метода решения и пробуем упростить выражение. Так как и числитель и знаменатель обращаются в ноль при х=1, то если разложить на множители эти выражения, можно будет сократить (х-1) и неопределенность исчезнет.
Разложим
числитель на множители:
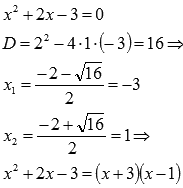
Разложим
знаменатель на множители:
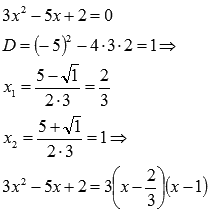
Наш
предел примет вид:
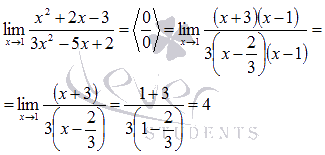
После преобразования неопределенность раскрылась.
Ответ:
![]()
Рассмотрим пределы на бесконечности от степенных выражений. Если показатели степенного выражения положительны, то предел на бесконечности бесконечен. Причем основное значение имеет наибольшая степень, остальные можно отбрасывать.
Пример.
![]()
Пример.
![]()
Если
выражение под знаком предела представляет
собой дробь, причем и числитель и
знаменатель есть степенные выражения
(m –
степень числителя, а n –
степень знаменателя), то при ![]() возникает
неопределенность вида бесконечность
на бесконечность
,
в этом случае неопределенность
раскрывается делением
и числитель и знаменатель на
возникает
неопределенность вида бесконечность
на бесконечность
,
в этом случае неопределенность
раскрывается делением
и числитель и знаменатель на ![]()
Пример.
Вычислить
предел 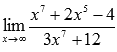
Решение.
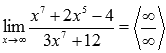 Степень
числителя равна семи, то есть m=7.
Степень знаменателя также равна семиn=7.
Разделим и числитель и знаменатель
на
Степень
числителя равна семи, то есть m=7.
Степень знаменателя также равна семиn=7.
Разделим и числитель и знаменатель
на ![]() .
.
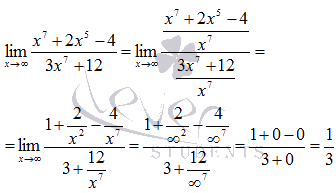
Ответ:
![]()
Пример.
Вычислить
предел 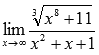
Решение.
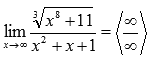 Степень
числителя 8/3,
степень знаменателя 2.
Разделим и числитель и знаменатель
на
Степень
числителя 8/3,
степень знаменателя 2.
Разделим и числитель и знаменатель
на ![]() .
.
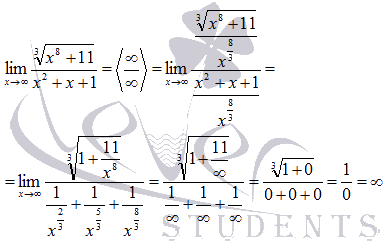
Ответ:
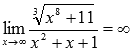
Пример.
Вычислить
предел 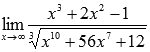
Решение.
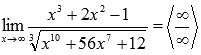 Степень
числителя 3,
степень знаменателя 10/3.
Разделим и числитель и знаменатель
на
Степень
числителя 3,
степень знаменателя 10/3.
Разделим и числитель и знаменатель
на![]() .
.
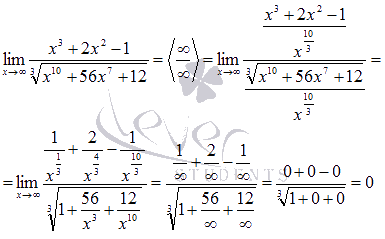
Ответ:
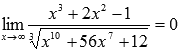
ВЫВОД.
Таким образом, возможны три варианта для предела отношения степенных выражений:
Если m равно n, то предел равен отношению коэффициентов при старших степенях;
Если m больше n, то предел равен бесконечности;
Если m меньше n, то предел равен 0.
