
- •Математический анализ 1 а.Ф.Чувенков
- •Программа по математическому анализу (с рекомендуемой литературой и основными теоретическими сведениями) Множества
- •Последовательности
- •Функции
- •Дифференцирование
- •Исследование функции
- •Литература
- •Задания для самостоятельного выполнения
- •Решение типового варианта
- •Латинский алфавит
- •Греческий алфавит
Решение типового варианта
Пример 1а.
Доказать равенство
![]() .
.
Решение. Для того, чтобы доказать равенство двух множеств нужно доказать вложения этих множеств друг в друга.
а). Докажем вложение
![]() .
Пусть
.
Пусть
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
б). Докажем вложение
![]() .
Пусть
.
Пусть
![]()
![]()
![]()
![]()
![]() .
.
Из а) и б) следует доказываемое равенство.
Пример
1б. Исходя
из определения предела последовательности,
доказать, что
![]() .
.
Решение.
По определению
предела последовательности нужно
доказать, что для любого малого числа
![]() можно найти такое натуральное число
можно найти такое натуральное число
![]() ,
что для всех номеров
,
что для всех номеров
![]() выполняется неравенство
выполняется неравенство
![]() .
Упростим левую часть последнего
неравенства. Имеем
.
Упростим левую часть последнего
неравенства. Имеем
![]()
![]()
![]()
![]() (для
(для
![]() ).
Далее
).
Далее
![]()
![]() .
Решим теперь неравенство
.
Решим теперь неравенство
![]() .
Имеем
.
Имеем
![]()
![]() .
Таким образом, неравенство
выполняется для номеров
.
Таким образом, неравенство
выполняется для номеров
![]() .
Следовательно, оно тем более выполняется
для
.
Следовательно, оно тем более выполняется
для
![]() ,
где
,
где
![]() – целая часть числа
.
– целая часть числа
.
Пример 2. Найти область определения функции
![]() .
.
Решение.
Корень четной степени имеет смысл от
неотрицательных чисел. Поэтому
![]() .
И так как это выражение стоит в знаменателе,
то
.
И так как это выражение стоит в знаменателе,
то
![]() .
Решим это неравенство методом интервалов:
.
Решим это неравенство методом интервалов:
![]()
![]()
![]() .
.
Решением является
интервал
![]()
![]() .
.
Функция
![]() определена при
определена при
![]() т. е.
т. е.
![]()
![]() .
.
Значит из интервала
нужно удалить точку
![]() .
Следовательно, область определения
данной функции является множество
.
Следовательно, область определения
данной функции является множество
![]() .
.
Пример 3. Найти
предел
![]() .
.
Решение.
Подставив
вместо
число
![]() ,
в числителе и знаменателе получим
,
в числителе и знаменателе получим
![]() ,
т.е. получается неопределенность
,
т.е. получается неопределенность
![]() .
Чтобы раскрыть эту неопределенность
разложим числитель и знаменатель на
множители:
.
Чтобы раскрыть эту неопределенность
разложим числитель и знаменатель на
множители:
а).
![]()
![]()
![]() ;
;
б).
![]()
![]()
![]() .
.
Тогда имеем
![]()
![]()
![]()
![]() .
.
Пример 4. Найти
предел
![]() .
.
Решение. Подставив
вместо
«бесконечно большое число»
![]() ,
в числителе и знаменателе получим
,
т.е. получается неопределенность
,
в числителе и знаменателе получим
,
т.е. получается неопределенность
![]() .
Чтобы раскрыть её разделим числитель
и знаменатель на наибольшую степень
.
Чтобы раскрыть её разделим числитель
и знаменатель на наибольшую степень
![]() .
Имеем
.
Имеем

![]() .
.
Пример
5. Найти
предел
![]() .
.
Решение. Здесь имеем неопределенность вида . Для её раскрытия избавимся от иррациональности в знаменателе, умножив и числитель и знаменатель дроби на сопряжённое выражение. Имеем
![]()
![]()
![]()
![]() .
.
Пример
6. Найти
предел
![]() .
.
Решение.
Подставив
вместо
число 0, получим неопределенность вида
.
Для её раскрытия воспользуемся
тригонометрическими формулами и первым
замечательным пределом:
![]() .
Имеем
.
Имеем




![]() .
.
Пример
7. Найти
предел
![]() .
.
Решение.
Вместо
подставив 0, получим неопределенность
вида
![]() .
Следовательно, нужно воспользоваться
вторым замечательным пределом:
.
Следовательно, нужно воспользоваться
вторым замечательным пределом:
![]() .
Имеем
.
Имеем
![]()
![]()
![]()
![]()
![]() .
.
Пример 8. Исследовать функцию
![]() на непрерывность
и построить её график.
на непрерывность
и построить её график.
Решение.
Данная
функция определена во всех точках оси
абсцисс, кроме точки
.
Функция
![]() состоит из элементарных функций, которые,
как известно, непрерывны в области
определения. Значит на непрерывность
нужно исследовать точки «стыка» и точку,
в которой функция не определена. Для
удобства сделаем следующую схему:
состоит из элементарных функций, которые,
как известно, непрерывны в области
определения. Значит на непрерывность
нужно исследовать точки «стыка» и точку,
в которой функция не определена. Для
удобства сделаем следующую схему:
a).
Исследуем точку
![]()
![]() .
Найдём пределы слева, справа и
.
Найдём пределы слева, справа и![]()
значение функции в этой точке:
![]()
![]() ,
,
![]()
![]() ,
,
![]() .
.
Вывод: Так как
односторонние пределы конечны и не
равны между собой, то в точке
разрыв первого рода. Скачок в этой точке
равен
![]() .
Так как предел справа совпадает со
значением функции, то в точке
функция непрерывна справа.
.
Так как предел справа совпадает со
значением функции, то в точке
функция непрерывна справа.
б). Исследуем точку
![]() .
Имеем
.
Имеем
![]()
![]() ,
,
![]()
![]() ,
функция
в точке
не определена.
,
функция
в точке
не определена.
Вывод: Так как односторонние пределы равны , то в точке разрыв второго рода.
в). Исследуем точку
.
Имеем
![]()
![]() ,
,
![]()
![]() ,
,
![]() .
.
Вывод: В точке односторонние пределы существуют и совпадают со значение функции в сомой точке. Значит в точке данная функция непрерывна.
Построим график данной функции.

Пример 9. Продифференцировать функцию
![]() .
.
Решение.
Данная
функция представляет собой алгебраическую
сумму нескольких функций. Поэтому
воспользуемся свойством производной
от суммы функций:
![]() .
Потом, воспользовавшись свойством
.
Потом, воспользовавшись свойством
![]() ,
приведём степенные функции к удобному
для применения формулы
,
приведём степенные функции к удобному
для применения формулы
![]() виду. Имеем
виду. Имеем
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Пример 10. Продифференцировать функцию
![]()
Решение. Воспользуемся последовательно формулами , , . Имеем

![]()
![]()
![]()
![]() .
.
Пример 11. Продифференцировать функцию
![]() .
.
Решение.
Воспользуемся
формулами
![]() ,
,
,
![]() ,
,
![]() .
Имеем
.
Имеем
![]()
![]()

![]()

![]() .
.
Пример 12.
Продифференцировать
функцию
![]() .
.
Решение.
Воспользуемся
формулами
![]() ,
,
,
,
![]() ,
,
![]() .
Имеем
.
Имеем


![]()
![]() .
.
Пример 13.
Продифференцировать неявно заданную
функцию
![]() .
.
Решение.
Продифференцируем
равенство
![]()
![]() ,
считая
функцией от
:
,
считая
функцией от
:
![]()
![]()
![]()

![]()
![]()
![]() .
Теперь найдем
.
Теперь найдем
![]() из этого уравнения:
из этого уравнения:
![]()
![]() .
.
Пример
14. Найти
производную функции
,
заданной параметрически:
![]() ,
,
![]() .
.
Решение.
Воспользуемся
формулой дифференцирования функции,
заданной параметрически:
 .
Имеем
.
Имеем
![]() ,
,
![]() .
Значит
.
Значит
![]()
![]()
![]()
![]() .
.
Пример
15. Для функции
и аргумента
вычислить
:
![]() .
.
Решение. Найдём последовательно первую, вторую и третью производные данной функции:
![]()
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]() .
.
![]()
![]()
![]()
![]() .
.
Теперь осталось
найти значение
![]() :
:
![]() .
.
Пример 16. Найти
точку на кривой
![]() ,
касательная в которой параллельна
прямой
,
касательная в которой параллельна
прямой
![]() .
.
Решение.
Обозначим
координаты искомой точки через
и
![]() .
Так как касательная параллельна данной
прямой, то их угловых коэффициенты
должны совпадать. Для того, чтобы
определить угловой коэффициент прямой
перепишем её уравнение в виде
.
Так как касательная параллельна данной
прямой, то их угловых коэффициенты
должны совпадать. Для того, чтобы
определить угловой коэффициент прямой
перепишем её уравнение в виде
![]() .
Значит угловой коэффициент прямой равен
2. Как известно, значение
.
Значит угловой коэффициент прямой равен
2. Как известно, значение
![]() производной функции
в точке
есть угловой коэффициент касательной,
проведенной к графику функции в точке
производной функции
в точке
есть угловой коэффициент касательной,
проведенной к графику функции в точке
![]() .
В нашем случае
.
В нашем случае
![]() .
Имеем
.
Имеем
![]()
![]()
![]()
![]() .
Так как искомая точка лежит на данной
кривой, получаем равенство
.
Так как искомая точка лежит на данной
кривой, получаем равенство
![]() .
Таким образом, относительно неизвестных
и
получена система уравнений:
.
Таким образом, относительно неизвестных
и
получена система уравнений:
![]()
![]()
![]() .
.
Пример
17. Тело
движется по прямой
по закону
![]()
![]() .
Определить скорость и ускорение движения
тела. В какие моменты времени оно меняет
направление движения?
.
Определить скорость и ускорение движения
тела. В какие моменты времени оно меняет
направление движения?
Решение.
Как известно,
первая производная функции, задающей
закон движения, есть скорость тела
![]() ,
а вторая производная – его ускорение
,
а вторая производная – его ускорение
![]() .
Тогда имеем
.
Тогда имеем
![]()
![]()
![]()
![]() ,
,
![]() .
Чтобы найти моменты времени, в которые
тело меняет направление движения, нужно
найти точки, в которых функция
.
Чтобы найти моменты времени, в которые
тело меняет направление движения, нужно
найти точки, в которых функция
![]() меняет знак. Для этого решим уравнение
меняет знак. Для этого решим уравнение
![]()
![]()
![]() .
Так как время неотрицательно, то делаем
вывод: тело меняет направление движения
в момент времени
.
Так как время неотрицательно, то делаем
вывод: тело меняет направление движения
в момент времени
![]() .
.
Пример 18. Найти
предел, используя правило Лопиталя:
![]() .
.
Решение.
Подставив
вместо
число 0, получим неопределенность вида
![]() .
Правило Лопиталя можно применить только
к неопределенностям вида
и
.
Чтобы свести неопределенность
к одной из указанных неопределенностей,
обозначим данный предел буквой
.
Правило Лопиталя можно применить только
к неопределенностям вида
и
.
Чтобы свести неопределенность
к одной из указанных неопределенностей,
обозначим данный предел буквой
![]() и прологарифмируем обе части:
и прологарифмируем обе части:
![]() ,
,
![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Таким образом,
![]() .
.
Пример 19.
Найти наибольшее и наименьшее значения
функции
![]() на
отрезке
на
отрезке
![]() :
:
Решение.
Найдем
значения функции в стационарных точках,
принадлежащих данному отрезку, и в
граничных точках. Из этих значений
выберем наибольшее и наименьшее. Имеем
![]()
![]() .
Точка
.
Точка
![]() не принадлежит отрезку
.
не принадлежит отрезку
.
![]() ,
,
![]() ,
,
![]() .
Следовательно,
.
Следовательно,
![]()
![]() ,
,
![]() .
.
Пример 20. Провести полное исследование функции
![]() и построить её
график:
и построить её
график:
Решение.
1).
Область определения.
![]()
![]() .
.
2). Чётность,
нечётность.
![]()
![]() функция – нечётная
график симметричен относительно начала
координат.
функция – нечётная
график симметричен относительно начала
координат.
3). Точки
пересечения с осями координат.
а).
![]()
![]() –
уравнение не имеет решения
график не пересекает ось
.
б).
–
уравнение не имеет решения
график не пересекает ось
.
б).
![]() график не пересекает ось
график не пересекает ось
![]() .
.
4). Монотонность.
![]()
![]() ,
,
![]()
![]()
![]() функция возрастает
на множестве
функция возрастает
на множестве
![]() и убывает на множестве
и убывает на множестве
![]() .
.
5). Экстремумы. В соответствии с монотонностью сделаем схему:

при
![]() – max,
при
– min.
– max,
при
– min.
![]() ,
,
![]()
![]() .
Следовательно,
.
Следовательно,
![]() – точка максимума,
– точка максимума,
![]() – точка минимума.
– точка минимума.
6). Выпуклость.
![]()
![]() график
функции на интервале
график
функции на интервале
![]() выпуклый вниз, на интервале
выпуклый вниз, на интервале
![]() выпуклый вверх.
выпуклый вверх.
7). Точки
перегиба.
Направление выпуклости графика функции
меняется при переходе через точку
![]() .
Но эта точка не принадлежит области
определения функции. Значит точек
перегиба нет.
.
Но эта точка не принадлежит области
определения функции. Значит точек
перегиба нет.
8). Асимптоты. а). Вертикальные асимптоты. Точка не входит в область определения функции. Исследуем поведение графика функции в окрестности этой точки. Если хотя бы один из односторонних пределов равен , то прямая (ось ) является вертикальной асимптотой.
![]() ,
,
![]() .
.
Значит ось – вертикальная асимптота.
б). Наклонные
асимптоты имеют вид
![]() ,
где
,
где
![]()
![]() ,
,
![]()
![]()
![]()
![]() .
Следовательно, прямая
.
Следовательно, прямая
![]() является наклонной асимптотой при
является наклонной асимптотой при
![]() .
.
9). График функции.

Выбор варианта контрольной работы № 1
Задания контрольной работы № 1 по математическому анализу выбираются по последним двум цифрам зачетной книжки студента-заочника
Приложения
Неопределенности
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
здесь через
![]() обозначены выражения, стремящиеся
соответственно к
.
обозначены выражения, стремящиеся
соответственно к
.
Пределы
1.

 ;
3.
;
3.
 ;
4.
;
4. .
.
Эквивалентные бесконечно малые

 ;
; ;
;
 ;
;
;
2.
![]() ;
;
Таблица производных
![]() ,
,
![]() ,
,
![]()
а). Свойства производных
I.
![]() ,
III.
,
III.
![]()
 ,
IV.
,
IV.
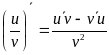
б). Формулы
1
9.
12.
16.
17.
18.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2.![]()
3.![]()
4.
![]()
4.1.
![]()
5.
![]()
5.1.
![]()
6.
![]()
7.
![]()
8.
![]()
