
- •Математический анализ 1 а.Ф.Чувенков
- •Программа по математическому анализу (с рекомендуемой литературой и основными теоретическими сведениями) Множества
- •Последовательности
- •Функции
- •Дифференцирование
- •Исследование функции
- •Литература
- •Задания для самостоятельного выполнения
- •Решение типового варианта
- •Латинский алфавит
- •Греческий алфавит
Литература
Кудрявцев Л.Д. Курс математического анализа. В трех томах. Том 1. М.: Высшая школа, 1988.
Кудрявцев Л.Д. Краткий курс математического анализа. М.: Наука, 1989.
Ильин В.А., Садовничий В.А., Сендов Бл.Х. Математический анализ. Начальный курс. М.: Изд. МГУ, 1985.
Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Том 1. М.: Наука, 1970.
Карташев А.П., Рождественский Б.Л. Математический анализ. М.: Наука, 1984.
Толстов Г.П. Элементы математического анализа. Том 1. М.: Наука, 1974.
Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. Том первый. М.: Наука, 1985.
Никольский С.М. Курс математического анализа. Том 1. М.: Наука, 1990.
Коровкин П.П. Математический анализ. Часть I. М., 1963.
Смирнов В.И. Курс высшей математики. Том первый. М.: Наука, 1965.
Шипачев В.С. Высшая математика. М.: Высшая школа, 1990.
Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. М.: Наука, 1980.
Уваренков И.М., Маллер М.З. Курс математического анализа. Том 1. М.: Просвещение, 1966.
Демидович Б.П. Сборник задач и упражнений по математическому анализу. М.: Наука, 1990.
Берман Г.Н. Сборник задач по курсу математического анализа. М.: Наука, 1985
Очан Ю.С. Сборник задач по математическому анализу. Общая теория множеств и функций. М.: Просвещение, 1981.
Кудрявцев Л.Д. и др. Сборник задач по математическому анализу. Предел, непрерывность, дифференцируемость. М.: Наука, 1984.
Виноградов И.А., Олехник С.Н., Садовничий В.А. Задачи и упражнения по математическому анализу. М.: Изд. МГУ, 1988.
Давыдов Н.А. и др. Сборник задач по математическому анализу. М.: Просвещение, 1973.
Виленкин Н.Я. и др. Задачник по курсу математического анализа. Часть 1. М.: Просвещение, 1971.
Гусак А.А Высшая математика. Том 1. Минск: Изд. БГУ, 1983.
Руководство к решению задач по высшей математике. Под ред. Е.И.Гурского. Часть 1. Минск: Вышэйшая школа, 1989.
Шипачев В.С. Курс высшей математики. Анализ функций одной переменной и аналитическая геометрия. М:. Изд. МГУ, 1981.
Дадаян А.А., Дударенко В.А. Математический анализ. Минск: Вышэйшая школа, 1990.
Шипачев В.С. Сборник задач по высшей математике. М.: Высшая школа, 1994.
Сборник индивидуальных заданий по высшей математике. Часть 1. Под общ. ред. А.П. Рябушко. Минск.: Вышэйшая школа, 1991.
Задания для самостоятельного выполнения
1. Доказать равенства:
 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
.
Исходя из определения предела последовательности, доказать, что:
|
2. Найти область определения функции:
|
|
3. Найти пределы:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Найти пределы:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. Найти пределы:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. Найти пределы:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7. Найти пределы:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. Исследовать функции на непрерывность и построить их графики:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9. Продифференцировать функции:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найти производные функций:
Продифференцировать функции:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12. Продифференцировать функции:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Продифференцировать неявно заданную функцию
 :
:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найти производную функции , заданной параметрически:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для функции
 и аргумента
и аргумента
 вычислить
вычислить
 :
:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Записать уравнение касательной к кривой
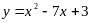 в точке с абсциссой
в точке с абсциссой
 .
.Записать уравнение касательной к кривой
 в точке с абсциссой
в точке с абсциссой
 .
.Записать уравнение касательной к кривой
 в точке
в точке
 .
.Записать уравнение касательной к кривой
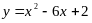 в точке с абсциссой
в точке с абсциссой
 .
.Записать уравнение касательной к кривой
 в точке с абсциссой
в точке с абсциссой
 .
.Записать уравнение касательной к кривой

 в точке с абсциссой
в точке с абсциссой
 .
.Записать уравнение касательной к кривой
 в точке с абсциссой
в точке с абсциссой
 .
.Записать уравнение касательной к кривой
 в точке с абсциссой
в точке с абсциссой
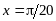 .
.Записать уравнение касательной к кривой
 в точке с абсциссой
в точке с абсциссой
 .
.Записать уравнение нормали к кривой
 в точке с абсциссой
.
в точке с абсциссой
.Записать уравнение нормали к кривой
 в точке с абсциссой
в точке с абсциссой
 .
.
Записать уравнение нормали к кривой
 в точке
в точке
 .
.Записать уравнение нормали к кривой
 в точке с абсциссой
.
в точке с абсциссой
.Записать уравнение касательной к кривой
 в точке с абсциссой
в точке с абсциссой
 .
.Определить угловой коэффициент касательной к кривой
 в точке
в точке
 .
.В какой точке кривой
 касательная перпендикулярна к прямой
касательная перпендикулярна к прямой
 ?
?Выяснить, в каких точках кривой
 касательная составляет с осью
касательная составляет с осью
 угол
угол
 .
.Выяснить, в какой точке кривой
 касательная составляет с осью
угол
касательная составляет с осью
угол
 .
.Выяснить, в какой точке кривой
 касательная составляет с осью
угол
касательная составляет с осью
угол
 .
.Выяснить, в какой точке кривой
 касательная составляет с осью
угол
.
касательная составляет с осью
угол
.Выяснить, в какой точке кривой
 касательная параллельна прямой
касательная параллельна прямой
 .
.Выяснить, в какой точке кривой
 касательная перпендикулярна прямой
касательная перпендикулярна прямой
 .
.Выяснить, в какой точке кривой
 касательная параллельна прямой
касательная параллельна прямой
 .
.Найти точки на кривой
 ,
в которых касательные параллельны оси
.
,
в которых касательные параллельны оси
.Найти точку на кривой
 ,
касательная в которой параллельна
прямой
,
касательная в которой параллельна
прямой
 .
.Найти точку на кривой
 ,
касательная в которой перпендикулярна
к прямой
,
касательная в которой перпендикулярна
к прямой
 .
.
Найти точку на кривой
 ,
касательная в которой параллельна
прямой
,
касательная в которой параллельна
прямой
 .
.Найти точку на кривой
 ,
касательная в которой перпендикулярна
к прямой
,
касательная в которой перпендикулярна
к прямой
 .
.Найти точку на кривой
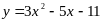 ,
касательная в которой параллельна
прямой
,
касательная в которой параллельна
прямой
 .
.Найти точку на кривой
 ,
касательная в которой параллельна
прямой
,
касательная в которой параллельна
прямой
 .
.
Траектория движения тела – кубическая парабола
 .
В каких ее точках скорости возрастания
абсциссы и ординаты одинаковы?
.
В каких ее точках скорости возрастания
абсциссы и ординаты одинаковы?Закон движения материальной точки
 .
В какой момент времени скорость ее
движения будет равна 2 м/с?
.
В какой момент времени скорость ее
движения будет равна 2 м/с?По оси движутся две материальные точки, законы движения которых
 и
и
 .
С какой скоростью эти точки удаляются
друг от друга в момент встречи?
.
С какой скоростью эти точки удаляются
друг от друга в момент встречи?Материальная точка движется по гиперболе
 так, что ее абсцисса
так, что ее абсцисса
 равномерно возрастает со скоростью 1
м/с. С какой скоростью изменяется
ордината точки, когда она проходит
положение
равномерно возрастает со скоростью 1
м/с. С какой скоростью изменяется
ордината точки, когда она проходит
положение
 ?
?В какой точке параболы
 ордината возрастает вдвое быстрее, чем
абсцисса?
ордината возрастает вдвое быстрее, чем
абсцисса?Закон движения материальной точки
 .
Найти скорость движения точки в момент
времени
.
Найти скорость движения точки в момент
времени
 с.
с.Закон движения материальной точки
 .
Найти скорость движения точки в момент
времени
с.
.
Найти скорость движения точки в момент
времени
с.Закон движения точки
 .
Найти ее скорость в момент времени
.
Найти ее скорость в момент времени
 с.
с.Закон движения точки
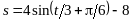 .
Найти ее скорость в момент времени
.
Найти ее скорость в момент времени
 с.
с.
Закон движения точки
 .
Найти ее скорость в момент времени
.
Найти ее скорость в момент времени
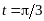 с.
с.Закон движения материальной точки
 .
В какой момент времени ее скорость
будет равна 42 м/с?
.
В какой момент времени ее скорость
будет равна 42 м/с?Закон движения материальной точки
 .
В какой момент времени ее скорость
будет равна 190 м/с?
.
В какой момент времени ее скорость
будет равна 190 м/с?Закон движения материальной точки
 .
Найти ее скорость в момент времени
.
Найти ее скорость в момент времени
 с.
с.Закон движения материальной точки
 .
Найти скорость ее движения в момент
времени
с.
.
Найти скорость ее движения в момент
времени
с.Закон движения материальной точки
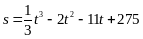 .
В какой момент времени скорость ее
движения будет равна 10 м/с?
.
В какой момент времени скорость ее
движения будет равна 10 м/с?По оси движутся две материальные точки, законы движения которых
 и
и
 .
С какой скоростью эти точки удаляются
друг от друга в момент встречи?
.
С какой скоростью эти точки удаляются
друг от друга в момент встречи?По оси движутся две материальные точки, законы движения которых
 и
и
 .
С какой скоростью эти точки удаляются
друг от друга в момент встречи?
.
С какой скоростью эти точки удаляются
друг от друга в момент встречи?По оси движутся две материальные точки, законы движения которых
 и
и
 .
В какой момент времени их скорости
окажутся равными?
.
В какой момент времени их скорости
окажутся равными?Материальная точка движется по гиперболе
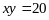 так, что ее абсцисса
равномерно возрастает со скоростью 1
м/с. С какой скоростью изменяется
ордината точки, когда она проходит
положение
так, что ее абсцисса
равномерно возрастает со скоростью 1
м/с. С какой скоростью изменяется
ордината точки, когда она проходит
положение
 ?
?В какой точке параболы
 ордината возрастает вдвое быстрее, чем
абсцисса?
ордината возрастает вдвое быстрее, чем
абсцисса?По оси движутся две материальные точки, законы движения которых
 и
и
 .
С какой скоростью эти точки удаляются
друг от друга в момент встречи?
.
С какой скоростью эти точки удаляются
друг от друга в момент встречи?
В какой точке кривой
 ордината возрастает в четыре раза
быстрее, чем абсцисса?
ордината возрастает в четыре раза
быстрее, чем абсцисса?В какой точке параболы
 абсцисса возрастает вдвое быстрее, чем
ордината?
абсцисса возрастает вдвое быстрее, чем
ордината?В какой точке параболы
 абсцисса возрастает вдвое быстрее, чем
ордината?
абсцисса возрастает вдвое быстрее, чем
ордината?По оси движутся две материальные точки, законы движения которых
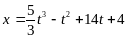 и
и
 .
В какой момент времени их скорости
окажутся равными?
.
В какой момент времени их скорости
окажутся равными?Закон движения материальной точки по прямой задан формулой
 .
В какой момент времени скорость точки
будет равна нулю?
.
В какой момент времени скорость точки
будет равна нулю?Тело движется по прямой по закону

 .
Определить скорость и ускорение движения
тела. В какие моменты времени оно меняет
направление движения?
.
Определить скорость и ускорение движения
тела. В какие моменты времени оно меняет
направление движения?Зависимость между массой кг вещества, получаемого в некоторой химической реакции, и времени
 выражается уравнением
выражается уравнением
 .
Определить скорость реакции в случае,
когда
.
Определить скорость реакции в случае,
когда
 с.
с.Материальная точка движется прямолинейно так, что
 ,
где
,
где
 –
скорость;
–
пройденный путь. Определить ускорение
движения точки в момент, когда скорость
равна 6 м/с.
–
скорость;
–
пройденный путь. Определить ускорение
движения точки в момент, когда скорость
равна 6 м/с.Закон движения материальной точки
 .
Найти скорость движения точки в момент
времени
с.
.
Найти скорость движения точки в момент
времени
с.
Найти пределы, используя правило Лопиталя:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найти наибольшее наименьшее значения функции
 на
отрезке
на
отрезке
 :
:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Провести полное исследование функции и построить её график:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

 ;
;