Математический анализ 1 а.Ф.Чувенков

Содержание

Программа по математическому анализу (с рекомендуемой литературой и основными теоретическими сведениями) 3

Множества 3

Последовательности 6

Функции 11

Дифференцирование 17

Исследование функции 26

Литература 30

Задания для самостоятельного выполнения 32

Решение типового варианта 49

Выбор варианта контрольной работы № 1 65

Приложения 65

Неопределенности 65

Пределы 65

Эквивалентные бесконечно малые 65

Таблица производных 66

Латинский алфавит 67

Греческий алфавит 67

Программа по математическому анализу (с рекомендуемой литературой и основными теоретическими сведениями) Множества

1. Множества: обозначения, символы , , , , , , 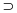, , . Теория: [1, стр. 18-19, 34-36], [2, стр. 11], [3, стр. 59-60], [5, стр. 7], [8, стр. 16], [11, стр. 10-11], [17, стр. 5-6, 26-27].

Понятие множества и его элементов являются первичными в математике. Множества обозначают большими буквами латинского алфавита; элементы множества – малыми буквами.

Если каждый элемент множества А является элементом множества В, то пишут . Множества А и В равны ( ), т.е. состоят из одних и тех же элементов, тогда и только тогда, когда и .

2. Операции над множествами: объединение, пересечение, разность, симметрическая разность, дополнение. Теория: [1, стр. 19-21], [2, стр. 11-12], [3, стр. 60, 65-67], [5, стр. 7-8], [8, стр. 18-19], [17, стр. 6-8]. Решённые примеры: [17, стр. 8], Задачи: [16, зад. 1-17], [17, зад. 1.1-1.19], [18, стр. 144].

– объединение;

– пересечение;

– разность;

– симметрическая разность;

– дополнение.

3. Числовые множества. Множество действительных чисел. Непрерывность множества действительных чисел. Теория: [1, стр. 26-31, 37-58], [2, стр. 15-18], [3, стр. 29-34, 46-52], [4, стр. 11-21, 24-25, 28-35], [5, стр. 13-17], [7, стр. 11-15], [8, стр. 16-17], [11, стр. 11-14], [17, стр. 36-39, 43-45], [21, стр. 262-263], Решённые примеры: [20, стр. 6].

– множество натуральных чисел;

– множество целых чисел;

– множество рациональных чисел;

Множество элементов, на котором определены операции сложения и умножения, удовлетворяющие некоторым свойствам (аксиомам), называется множеством действительных чисел и обозначается через .

Одним из указанных свойств является аксиома непрерывности множества действительных чисел: для любых непустых подмножеств X и Y множества таких, что для каждой пары чисел и выполняется неравенство , существует число а, удовлетворяющее условию , , .

4. Числовая прямая, окрестности. Теория: [1, стр. 61-64], [2, стр. 18-20], [3, стр. 52-53], [7, стр. 17-18], [11, стр. 14-16], [17, стр. 39-40], [21, стр. 263-264]. Задачи: [17, зад. 3.14-316], [25, стр. 5].

Геометрически множество действительных чисел изображается направленной (ориентированной) прямой, а отдельные числа – точками этой прямой.

Удобно дополнить множество действительных чисел элементами, обозначаемыми и и называемыми плюс бесконечность и минус бесконечность.

– отрезок.

– интервал.

, – полуинтервалы.

-окрестностью числа a называется интервал , т.е. .

5. Ограниченные и неограниченные множества. Теория: [1, стр. 64-67], [2, стр. 57], [3, стр. 40-41], [4, стр. 25-26], [5, стр. 19], [7, стр. 19], [8, стр. 75-76, 91-93], [17, стр. 50], [21, стр. 264-265]. Задачи: [17, зад. 3.47-3.49], [25, стр. 5-7].

Множество называется ограниченным сверху (снизу), если существует такое число M (m), что для всех имеет место неравенство ( ).

X – огр. сверху (снизу) .

6. Верхняя и нижняя грани. Теорема о существовании верхней (нижней) грани у ограниченного сверху (снизу) множества. Теория: [1, стр. 67-74], [2, стр. 57-59], [3, стр. 41-43], [4, стр. 26-28], [5, стр. 19-21], [8, стр. 76-77], [11, стр. 17-18], [17, стр. 50-51], [21, стр. 265-266]. Решённые примеры: [20, стр. 6-7]. Задачи: [14, зад. 15-20], [17, зад. 3.50-3.54], [20, зад. 20.1-22.1], [25, стр. 5-7].

Пусть числовое множество X ограничено сверху. Наименьшее среди всех чисел, ограничивающих сверху множество X, называется его верхней гранью и обозначается или .

Если числовое множество X ограничено снизу, то наибольшее среди всех чисел, ограничивающих снизу множество X, называется его нижней гранью и обозначается или .

Всякое ограниченное сверху непустое числовое множество имеет верхнюю грань, а всякое ограниченное снизу непустое числовое множество имеет нижнюю грань.

7. Принцип вложенных отрезков. Теория: [1, стр. 75-80], [2, стр. 62-64], [3, стр. 85-86], [4, стр. 82-83], [5, стр. 17], [8, стр. 90-91], [11, стр. 33-34], [17, стр. 51], [21, стр. 263]. Задачи: [17, зад. 3.55-3.57].

Система числовых отрезков , , , , называется системой вложенных отрезков, если , т. е. .

Всякая система вложенных отрезков имеет непустое пересечение.

Длины отрезков , , , называется стремящимися к нулю, если для любого числа существует такой номер , что для всех номеров выполняется неравенство .

Для всякой системы вложенных отрезков , длины которых стремятся к нулю, существует единственная точка , принадлежащая всем отрезкам данной системы, при этом .