2. Определители.

Каждой квадратной матрице n–го порядка А можно поставить в соответствие некоторое число – определитель n–го порядка (│А│, D(A), detA, ∆(A), ∆ - обозначения), который вычисляется по определенному правилу. Далее мы сформулируем это правило – « разложение определителя по любой строке (столбцу) » – с помощью индукции.

Пусть n=2.

.

Например, =21-4(3)=2+12=14.

Пусть n=3.

Минором M_ij, соответствующим элементу a_ij матрицы А, называется определитель, получающийся из матрицы А после вычеркивания i–ой строки и j–го столбца, на пересечении которых стоит элемент a_ij; i=1, 2, …, n; j=1, 2, …, n:

Алгебраическим дополнением A_ij элемента a_ij матрицы А называется величина:

A_ij = (–1)^{i+ j}M_ij , например: А₁₁=М₁₁, А₁₂=-М₁₂, … .

Если сумма индексов четная, то множитель перед минором дает знак «+», если нечетная «–». Распределение знаков иллюстрируется матрицей

.

Определение 2.2. Правило вычисления определителя по любой строке (столбцу) матрицы:

1 вариант (по 1-й строке):

│А│= а₁₁А₁₁+а₁₂А₁₂+а₁₃А₁₃ = а₁₁М₁₁–а₁₂М₁₂+а₁₃М₁₃;

2 вариант (по 2–му столбцу):

│А│= а₂₁А₂₁+а₂₂А₂₂+а₂₃А₂₃ = а₂₁М₂₁+а₂₂М₂₂–а₁₃М₁₃.

Аналогичным образом определяется и вычисляется определитель n-го порядка: сводится к вычислению n определителей (n–1)-го порядка.

Пример 1.

а). Разложим определитель по 1-ой строке:

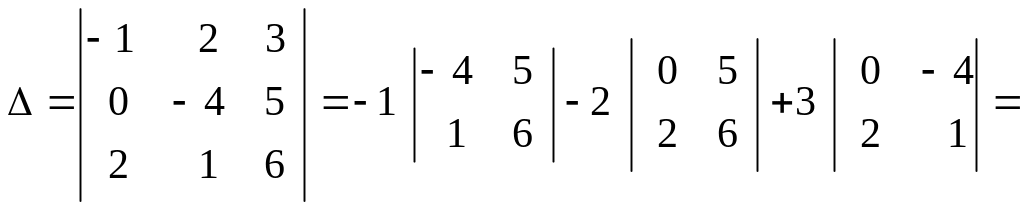
= (-1)(-24-5)-2(0-10)+3(0+8)=29+20+24=73.

б). Разложим определитель по 2-ой строке:

=4(66)5(14)=73.

Свойства определителей (на примерах определителей 2-го порядка).

Величина определителя:

1) не меняется, если матрицу A транспонировать, то есть строки заменить соответствующими столбцами: А*

2) меняет знак, если у него переменить местами две строки (столбца):

3) умножается на число k, если элементы строки (столбца) умножить на k:

то есть общий множитель в строке (столбце) можно выносить за знак определителя;

4) равна нулю, если элементы любого столбца (строки) равны нулю:

0b₂0b₁= 0;

5) равна нулю, если имеются равные строки (столбцы):

a₁a₂a₂a₂= 0;

6) не изменится, если к элементам любой строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на число k:

,

(к I-й строке (столбцу) прибавить 2-ю строку (столбец), умноженную на число k – рекомендуем кратко записывать так: kс₂+с₁ (kсТ₂+сТ₁);

7) равна произведению элементов стоящих на диагонали, если матрица диагональная или треугольного вида:

(убедитесь в этом, разложив определитель по 1-му столбцу).

8). Определитель от произведения АВ квадратных матриц А, В равен произведению определителей от каждой матрицы А, В: │АВ│=│А││В│.

Рекомендуем проверить все свойства определителя на конкретных матрицах.

Естественно, определители n-го порядка удовлетворяют всем свойствам 1)–8).

Вычисление определителей большого порядка согласно Определения 2 достаточно трудоемкая операция, поэтому, пользуясь свойствами определителей, приводят матрицу к треугольному виду и затем вычисляют определитель согласно пункта 7).

Пример 2. Вычислим определитель из примера 1 указанным способом. Последовательно в столбцах ниже главной диагонали « превратим » элементы определителя в нули. Первую строку, умноженную на 2, прибавим к 3-ей ( 2с₁+с₃ ), получим:

Умноженную на 5 строку 2, прибавим к умноженной на 4 строке 3 (5с₂+4с₃). Так как от умножения строки 3 на 4 определитель увеличивается в 4 раза, впереди поставим множитель :

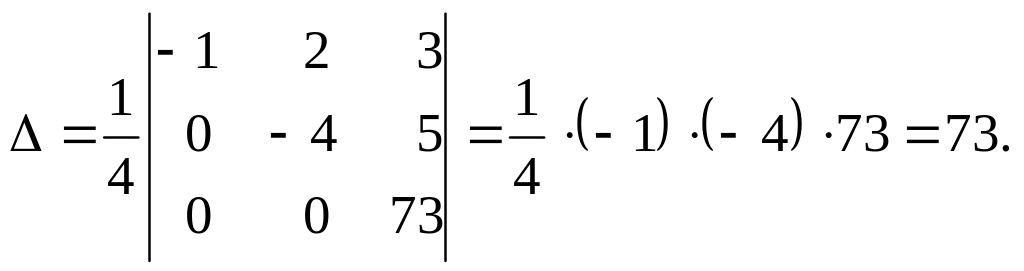
Пример 3.

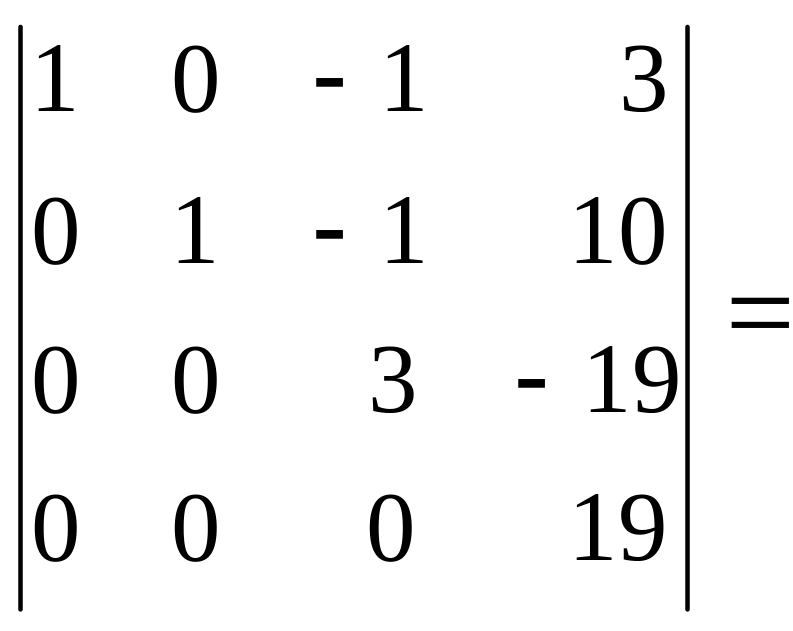
319=19.

Определители играют важную роль при решении систем линейных уравнений, во многих других разделах математики в первую очередь, в геометрии и в математическом анализе.