3.3 Примеры математических моделей задач линейного программирования

Наиболее разработанной и простой частью математического программирования является линейное программирование в силу достаточной изученности линейных функций и возможности прогнозирования их поведения.

3.3.1 Задача об использовании или распределении ресурсов

Пусть некоторое предприятие выпускает n видов изделий, для которых необходимо k видов ресурсов, чьи запасы имеются в количествах . Для выпуска каждого вида изделия известны технологические коэффициенты означающие количество i-го ресурса, затрачиваемого на выпуск j-го изделия. Кроме того, известна прибыль , получаемая от реализации j-го вида изделия. На планируемый период все коэффициенты остаются неизменными. Составить такой план выпуска изделий, при котором прибыль от реализации продукции была бы максимальной.

Это условие задачи, представленное в текстовой форме. Составим математическую модель задачи.

Пусть - количество единиц изделий j-го вида. Тогда прибыль, полученная от реализации всего количества произведенной продукции, будет выражена в виде целевой функции F(х). А ограниченные ресурсы и технологические коэффициенты позволяют построить систему ограничений. Получим математическую модель задачи:

Пример. Мебельная фабрика выпускает 3 вида изделий: шкафы, столы и стулья. В процессе их изготовления используются фрезерные, сверлильные и шлифовальные станки.

Причем в процессе изготовления шкафа фрезерный станок работает 0,25 ч, сверлильный - 0,18 ч, шлифовальный - 0,24 ч; стола: фрезерный - 0,2 ч, сверлильный - 0,13 ч, шлифовальный - 0,19 ч; стула: фрезерный 0,3 ч, сверлильный – 0,11 ч, шлифовальный -0,14 ч. Ресурс рабочего времени станков: фрезерного- 250 ч, сверлильного - 300 ч, шлифовального - 320 ч. Согласно плановому заданию, необходимо изготовить не менее 150 шкафов, столов - более 200, стульев - более 400. Прибыль за каждый шкаф составляет 5 ден. eд., за стол - 3 ден. ед., за стул - 2 ден. ед.

Требуется составить такой план выпуска изделий, при котором требуемые объемы по каждому виду изделий были бы выполнены, ресурсы времени по каждому виду оборудования не превышены, полученная прибыль была бы максимальной.

Решение. Пусть - количество шкафов, - количество столов, - количество стульев. Построим математическую модель задачи.

Система ограничений примет вид

Прибыль (целевая функция) составляет:

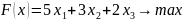
3.3.2 Задача составления смесей

Пусть для некоторых нужд, например кормления, требуется составить 2 вида корма, стоимость единицы каждого из которых и . В каждом виде корма должны присутствовать питательные вещества , для которых известно, что в норме их должно быть не менее единиц соответственно. Кроме того, известны технологические коэффициенты - количество i-го питательного вещества в j-м виде корма. Требуется составить такой рацион питания, при котором стоимость корма была наименьшей, а количество питательных веществ не было бы меньше нормы.

Пусть - количество единиц корма каждого вида.

Пример. На свиноферме производится откорм свиней. Известно, что каждая должна получать не менее 6 единиц вещества , не менее 8 - , не менее 12 - . Существуют 3 вида кормов.

Информация по стоимости этих кормов и содержанию единиц каждого вещества в единице корма находится в таблице:

Вид корма	Вещества			Стоимость вида корма
1	2	1	3	2
2	1	2	4	3
3	3	1,5	2	2,5

Требуется обеспечить наиболее дешевый рацион питания животных в виде комбикорма.

Решение. Пусть - количество единиц корма каждого вида. Тогда математическая модель задачи имеет вид: