12. Лекция № 12

12.1. Метод Ньютона

Решение нелинейных алгебраических и трансцендентных уравнений методом Ньютона. Его основное достоинство состоит, в том, что при сравнительно несложной схеме вычисления он обладает быстрой сходимостью. Метод Ньютона универсален и пригоден для решения обширного класса нелинейных задач.

Идея метода Ньютона состоит в последовательной замене на каждой итерации нелинейной системы уравнений некоторой линейной, решение которой дает значения неизвестных, более близкие к решению нелинейной системы, чем исходное приближение. Поясним идею этого метода на примере решения уравнения [3]:

. (12.1)

Р ешение данного уравнения X - это точка, в которой кривая проходит через нуль (рис.12.1). Зададим начальное приближение .

Заменим уравнение (12.1) в окрестности точки линейным уравнением:

, (12.2)

левая часть, которого представляет собой два первых члена разложения функции в ряд Тейлора. Решим линейное уравнение (12.2) и определим поправку к начальному приближению:

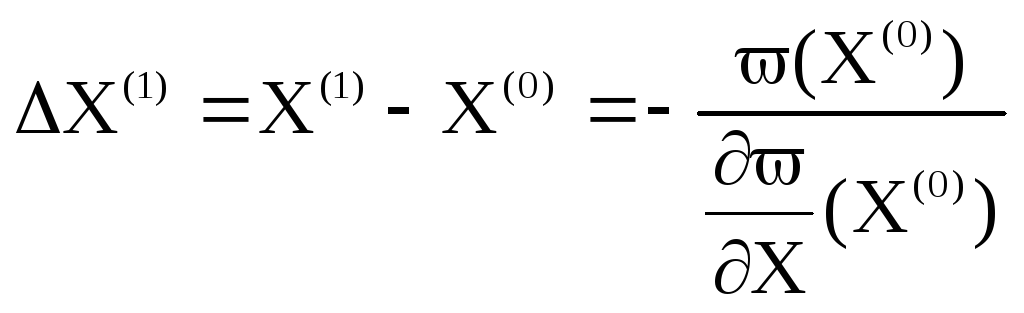. (12.3)

За новое приближение неизвестного принимаем:

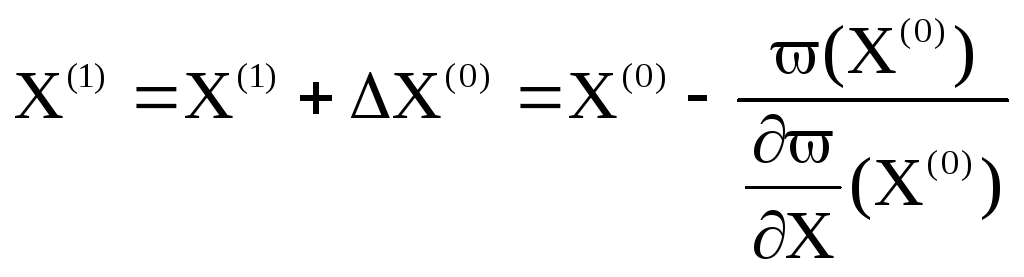. (12.4)

Аналогично определяются следующие приближения:

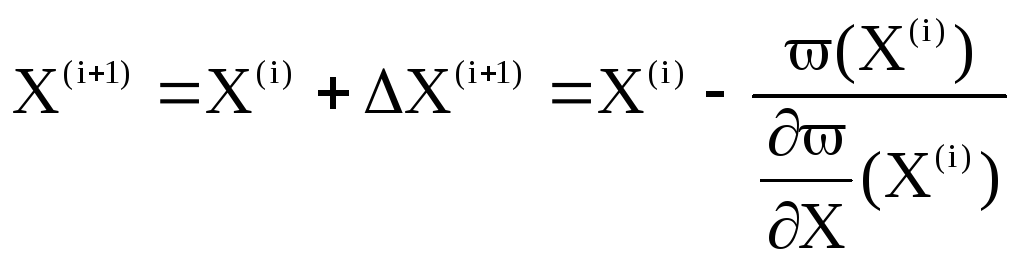. (12.5)

Итерационный процесс сходится, если функция становится близкой к нулю. Сходимость считается достигнутой, если невязка (или небаланс) меньше заданной, то есть при

. (12.6)

Отметим, что контроль сходимости по поправке может привести к неверным результатам.

Дадим геометрическую интерпретацию метода Ньютона (рис.12.1). Один шаг метода Ньютона сводится к замене кривой на прямую

, которая является касательной к этой кривой в точке . Поэтому метод Ньютона называют также методом касательных. Приближение есть точка пересечения касательной к кривой в точке с осью X.

Рассмотрим решение по методу Ньютона системы действительных нелинейных алгебраических уравнений [3]:

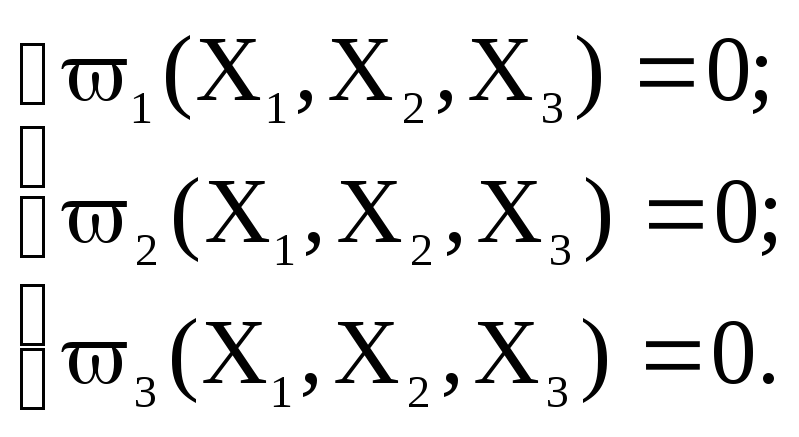(12.7)

Если использовать вектор-столбец X и вектор-функцию W(X), где

X=,W(X)=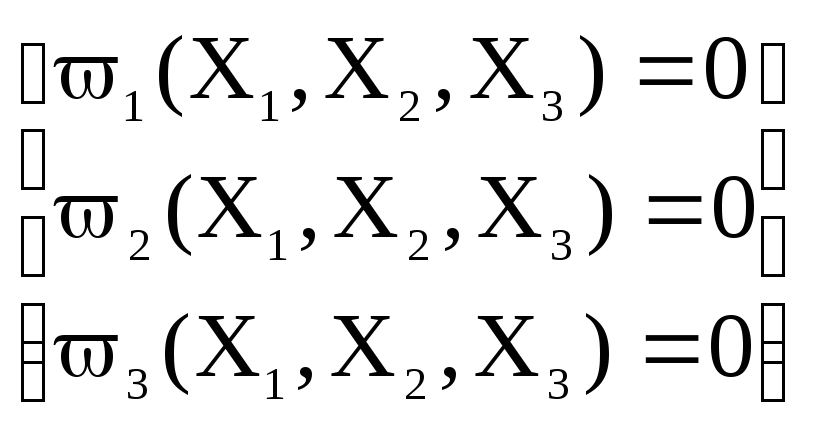, (12.8)

то систему (12.8) можно записать в матричном виде:

. (12.9)

Пусть - начальные приближения неизвестных. Заменим каждое из нелинейных уравнений (12.7) линейным, полученным разложением в ряд Тейлора. Например, первое уравнение после линеаризации будет иметь следующий вид:

12.10)

Запишем матрицу Якоби, то есть матрицу производных системы функций по переменным:

, (12.11)

Тогда систему линеаризованных уравнений можно записать в матричном виде следующим образом:

. (12.12)

Эта система линейна относительно поправок . Предположим, что - матрица Якоби не вырождена, то есть ее определитель не равен нулю.

Решим линейную систему (12.12) и определим поправки, например, методом Гаусса. Затем найдем первое приближение переменных:

. (12.13)

Каждый шаг итерационного процесса состоит в решении линейной системы:

(12.14)

и определении следующего приближения неизвестных:

, (12.15)

Часто итерационный процесс Ньютона записывают в матричной форме:

. (12.16)

Эта запись ни в коем случае не предполагает, что по методу Ньютона вычисляется обратная матрица и затем умножается на вектор . Поправки всегда определяются в результате решения линейной системы (12.14) по Гауссу (или в некоторых случаях по методу Зейделя) а выражение (12.16) используется для удобства записи и анализа итерационного процесса Ньютона. Контроль сходимости осуществляется по вектору невязок, то есть условие

(12.17)

должно выполняться для всех невязок (небалансов).