16 Вопрос Потоки Пальма и Эрланга

Разберем некоторые смежные понятия. Поток Пальма — это поток событий, которые предполагает, что интервалы времени между последовательными событиями:

 

являются одинаково распределенными величинами, которые не предусматривают зависимости.

Простейший поток — это частный случай потока Пальма. Здесь расстояния  есть случайные величины, распределение которых осуществляется в соответствии с одним и тем же показательным законом. Их независимость основывается на том, что простейший поток представлен в качестве потока без последствий, и расстояние по времени между любыми двумя событиями не зависят от расстояния других событий.

На практике часто встречаются такие потоки, которые могут быть приближенно заменены потоками Пальма.

В качестве образцов потоков Пальма могут быть представлены потоки Эрланга, которые возникают при осуществлении «просеивания» простейших потоков.

Скажем, если на оси   из существующих точек оставить каждую вторую (процесс просеивания), то опять возникнет поток событий. Его и называют потоком Эрланга второго порядка.

В целом, под потоком Эрланга  -го порядка  понимают поток, образующийся при сохранении в простейшем потоке каждой точки и исключении остальных. Таким образом, простейший поток — это частный случай Эрланга, то есть поток Эрланга первого порядка ( ).

Промежуток времени  -го порядка это ничто иное, как сумма независимых случайных расстояний между событиями в начальном простейшем потоке:

 

 

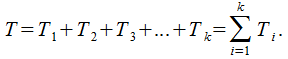
Распределение всех случайных величин осуществляется в соответствии с показательным законом (5.17).

Закон распределения интервала - это закон Эрланга  -го порядка.

Представим выражение для матожидания, дисперсии и среднего квадратичного отклонения для интервала событий в потоке Эрланга  -го порядка:

 

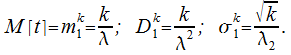
Нестационарный пуассоновский поток

Если поток событий нестационарный, то его основной характеристикой является мгновенная плотность  . Мгновенной плотностью потока называется предел отношения среднего числа событий, приходящихся на элементарный участок времени  , к длине этого участка, когда последний стремится к нулю:

,

где   - математическое ожидание числа событий на участке  .

Рассмотрим поток однородных событий, одинарный и без последействия, но не стационарный, с переменной плотностью  . Такой поток называется нестационарным пуассоновским потоком. Это первая ступень обобщения по сравнению с простейшим потоком.

Для такого потока число событий, попадающих на участок длины  , начинающийся в точке  , подчиняется закону Пуассона:

, 

где   - математическое ожидание числа событий на участке от   до  , равное

.

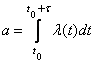Анализ данного выражения показывает, что величина   зависит не только от длины участка  , но и от его положения на оси  .

Найдем для этого потока закон распределения промежутка времени   между соседними событиями. Допустим, что в момент времени   появилось событие (точка на числовой оси  ). Тогда закон распределения времени    между этим событием и следующим будет иметь вид

,

где   - вероятность того, что на участке времени от   до   не появится ни одного события:

,  ,

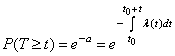откуда

,  .

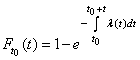Дифференцируя данное выражение, найдем ПРВ

,  .

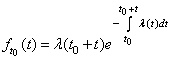Полученный закон распределения уже не будет показательным. Вид его зависит от параметра   и вида функции  . Например, при линейном изменении  , ПРВ будет иметь вид

,  .

Несмотря на то, что структура нестационарного пуассоновского потока несколько сложнее простейшего, он остается удобным для практических применений: главное свойство простейшего потока – отсутствие последействия – в нем сохранено. Это значит, что для произвольной фиксированной точки   закон распределения   времени   не будет зависеть от того, что происходило на участке времени  .