5. Временные характеристики.

а) переходная характеристика h(t) переходная функция;

б) импульсная переходная характеристика (t) функция веса.

Переходной характеристикой h(t) называется переходный процесс, возникающий на выходе звена при подаче на вход звена единичного ступенчатого воздействия при нулевых начальных условиях.

Ф ункция веса (t) переходящий процесс, возникающий на выходе звена при подаче на вход звена идеального импульса при нулевых начальных условиях.

6.Частотные характеристики сау.

Частотными называются характеристики звеньев (систем) в форме графиков или таблиц, отображающие изменение амплитуды и фазы выходной функции (т.е. реакцию) звеньев или систем относительно синусоидального входного воздействия в установившемся режиме при изменении частоты от 0 до . Очевидно, что при экспериментальном определении частотных характеристик диапазон изменения частоты входного гармонического воздействия ограничен техническими возможностями аппаратуры. Для линейных систем справедлив ПРИНЦИП СУПЕРПОЗИЦИИ, который можно сформулировать следующим образом.

Реакция системы на несколько одновременно действующих входных воздействий равна сумме реакций на каждое воздействие в отдельности.

Это позволяет ограничиться изучением систем только с одним входом.

1. Передаточная функция звена (W(p)).

2. Амплитудно-фазовая характеристика (АФХ).

3. Амплитудно-частотная характеристика (АЧХ).

4. Фазо-частотная характеристика (ФЧХ).

5. Логарифмическая амплитудно-частотная характеристика (ЛАЧХ).

Передаточная функция звена (w(p)).

Э то отношение прямого преобразования Лапласа сигнала на выходе звена к прямому преобразованию Лапласа входного сигнала при нулевых начальных условиях.

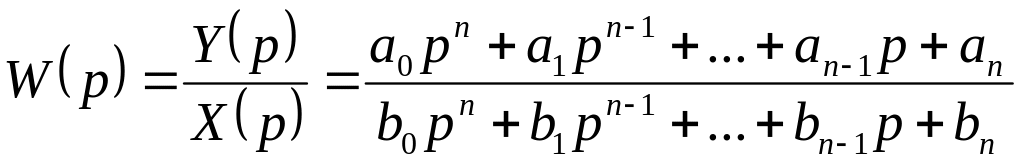
А фх. Если параметру p придать значение j, где и в передаточной функции заменить все p , то получим:

1. алгебраическая:

2. п оказательная:

A()модуль АФХ

()аргумент АФХ.

Переход:

АФХ отношение амплитуды выходного сигнала к амплитуде входного сигнала. () угол сдвига выходного сигнала по отношению к входному.

АФХ строится в комплексной плоскости:

Изменяем  от  до + , фиксируем Re, Im. По ним выстраивается график.

АЧХ

изображается в осях A(), .

Ф ЧХ:

Поскольку диапазон изменения частот велик, то прибегают к масштабированию оси частот:

Отрезок, в течении которого частота меняется в 10 раз называется декадой.

7 Логарифмические частотные характеристики .

П ри практических расчетах автоматических систем удобно использовать частотные характеристики, построенные в логарифмической системе координат. Такие характеристики называют логарифмическими. Они имеют меньшую кривизну и поэтому могут быть приближенно заменены ломаными линиями, составленными из нескольких прямолинейных отрезков. Причем, эти отрезки в большинстве случаев удается построить без громоздких вычислений при помощи некоторых простых правил. Кроме того, в логарифмической системе координат легко находить характеристики различных соединений элементов, так как умножению и делению обычных характеристик соответствует сложение и вычитание ординат логарифмических характеристик.

За единицу длины по оси частот логарифмических характеристик принимают декаду. Декада – интервал частот, заключенный между произвольным значением _i и его десятикратным значением 10_i. Отрезок логарифмической оси частот, соответствующий одной декаде, равен 1.

Обычно в расчетах используют логарифмическую амплитудную частотную характеристику (ЛАЧХ)

ординаты которой измеряют в логарифмических единицах – белах (Б) или децибелах (дБ).

При построении фазовой частотной характеристики логарифмический масштаб применяют только для оси абсцисс.

На рис.г показаны ЛАЧХ L() (толстая линия) и соответствующая ей приближенная (асимптотическая) характеристика L_а() в виде прямолинейных отрезков (тонкая линия). Частоты, соответствующие точкам стыковки отрезков, называют сопрягающими и обозначают _с.