
Практичне заняття №1,2
Тема: Кінематика матеріальної точки при прямолінійному русі
Опрацювати теоретичний матеріал лекції №1
Контрольні запитання
Що можна вважати матеріальною точкою: Місяць, Землю, рухомий автомобіль?
Вкажіть на рис. 1 вектор переміщення тіла, що рухається уздовж кривої АВ.

Рис. 1.1
В якому випадку пройдений тілом шлях у першу секунду дорівнює половині прискорення?
Побудуйте залежність координати матеріальної точки x від часу t при додатних x0 і v0 у випадку, коли прискорення a постійне і від’ємне.
Побудуйте залежність v від t для частинки, що рухається із стану спокою з прискоренням, зміна якого з часом представлена на рис. 1.3

Рис. 1.2
Усі зірки, зокрема деяка зірка N, віддаляються від Сонця із швидкостями, пропорційними їхнім відстаням до нього. Як буде виглядати ця картина з “точки зору” зірки N?
Три точки знаходяться у вершинах рівнобічного трикутника із стороною а=20 см. Вони розпочинають одночасно рухатися з постійною за модулем швидкістю v=5 мм/с так, що перша точка весь час тримає шлях на другу, друга – на третю, третя – на першу. Нарисувати траєкторії цих точок. З побудованого рисунка визначити, через який час точки зустрінуться. Аналітично визначити час .
Які кінематичні фактори визначають довжину стрибка спортсмена?
Вказівки до розв’язання задач
Для вирішення вказаних задач треба добре орієнтуватися в елементах кінематики матеріальної точки, знати визначення миттєвої швидкості та прискорення.
У табл. 1 наведено деякі кінематичні величини й формули.
Таблиця 1. Деякі кінематичні величини й формули
Фізична величина |
Формула |
||
Шлях s, м |
Рівномірний рух |
s = v t |
|
Швидкість v, м/c |
v=const |
||
Прискорення а, м/c2 |
а=0 |
||
s |
Рівноприскорений рух |
s = v0 t |
|
v |
v= v0 +at |
||
a |
а= const |
||
s |
Нерівномірний рух |
s = s(t) |
|
v |
v |
||
a |
а |
||
Приклади розв’язання задач
Задача 1. Лебідь, рак а щука тягнуть воза. Швидкість щуки у два рази менша від швидкості лебедя та в два рази більша швидкості рака. У деякий момент часу мотузки, які зв’язують воза й тварин лежать у горизонтальній площині й мають однакові напрямки як і швидкості відповідних тварин. Причому кут між швидкостями лебедя й щуки дорівнює α. Як при цьому має бути направлена швидкість рака?
Розв’язок:

Проекція швидкості воза на напрямок будь-якої з мотузок має дорівнювати швидкості тварина, яка тягне за цю мотузку, оскільки довжина будь-якої мотузки стала.
Нехай
швидкість рака дорівнює
 ,
тоді швидкість щуки дорівнює
,
тоді швидкість щуки дорівнює
 ,
а швидкість лебедя
,
а швидкість лебедя
 .
Будемо відкладати вектори цих швидкостей
з однієї точки А
й проведемо коло через кінці В
й С
векторів швидкостей лебедя й щуки, кут
між якими за умовою дорівнює α
(див. рис.). Оскільки вписані в коло
трикутники, що опираються на її діаметр,
є прямокутними, то вектор швидкості
воза є діаметром цього кола. При цьому
можливі наступні варіанти.
.
Будемо відкладати вектори цих швидкостей
з однієї точки А
й проведемо коло через кінці В
й С
векторів швидкостей лебедя й щуки, кут
між якими за умовою дорівнює α
(див. рис.). Оскільки вписані в коло
трикутники, що опираються на її діаметр,
є прямокутними, то вектор швидкості
воза є діаметром цього кола. При цьому
можливі наступні варіанти.
1) Вектор
швидкості воза лежить між векторами
швидкостей лебедя й щуки. Це можливо
при
 .
За теоремою косинусів для трикутника
АВС
будемо мати:
.
За теоремою косинусів для трикутника
АВС
будемо мати:
 .
.
По теоремі синусів діаметр кола, в яке вписано трикутник АВС, дорівнює:

При
цьому швидкість рака, як видно з малюнка,
може бути направлена під кутом
 ,
або
,
або
 до швидкості лебедя:
до швидкості лебедя:




2)
Вектор
швидкості воза не лежить між векторами
швидкостей лебедя й щуки. Це можливо
при
 .
Аналогічно, як і в попередньому випадку:
.
Аналогічно, як і в попередньому випадку:




3)
При
 ,
як видно з малюнка
,
як видно з малюнка
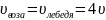 ,
і
,
і
 .
.
4)
При
 та
та
 задача не має розв’язків.
задача не має розв’язків.
Відповідь: 1) При
,
1) При
,
3) При , як видно з малюнка , і
.
4) При та задача не має розв’язків.
Задача 2. Знайти швидкість човна відносно берега річки, який пливе під кутом =30 до течії, якщо швидкість течії річки v1=1,5 м/с, швидкість човна відносно води v2=2,5 м/с.
Дано: Розв’язок:
= 30
|
|
|
Швидкість
човна відносно берега є векторною сумою
швидкостей
 :
:
 (див. рис. 1.4).
(див. рис. 1.4).
За
теоремою косинусів знайдемо модуль
вектора швидкості
 :
:
 ;
;

 .
.
Показаний на рис. 1.4 кут визначає напрямок вектора швидкості :
 ,
,
 .
.
Відповідь:
 ,
.
,
.
Задача
3.
Рух матеріальної точки задано рівняннями:
 ,
,
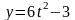 ,
,
 ,
де x,
y,
z
– координати, м.
визначити модулі швидкості
,
де x,
y,
z
– координати, м.
визначити модулі швидкості
 і прискорення а.
і прискорення а.
Дано:
|
Швидкість матеріальної точки:
|
– ? а – ? |
Відповідь:
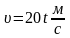 ;
;
 .
.
Задача 3. Вільно падаюче тіло за останні 2 с польоту пройшло 196 м шляху. З якої висоти воно впало?
Дано: t=t2 – t1 = 2 c s = 196 м |
Розв’язок: Нехай у момент часу t=0 c координата y тіла дорівнює y = h метрів, а в моменти часу t= t1 c і t= t2 c – y = s м і y = 0 м відповідно (див. рис.). |
h – ? |
Р ух
тіла відбувається у полі тяжіння Землі,
тому прискорення тіла – це прискорення
вільного падіння g =9,8 м/с2.
Кінематична формула залежності координати
y
від часу
ух
тіла відбувається у полі тяжіння Землі,
тому прискорення тіла – це прискорення
вільного падіння g =9,8 м/с2.
Кінематична формула залежності координати
y
від часу
 . (1.1)
. (1.1)
За
умовою задачі початкова координата
y0 =h м,
початкова швидкість v0 =0
м/с,
прискорення
 м/с2.
Записавши формулу (1.1) для моментів часу
t= t1 c
і t= t2 c,
а також вираз з умови
t2 – t1 = 2 c,
отримаємо систему трьох алгебраїчних
рівнянь з трьома невідомими h,
t1 і
t2
,
розв’язавши яку, знайдемо відповідь
задачі:
м/с2.
Записавши формулу (1.1) для моментів часу
t= t1 c
і t= t2 c,
а також вираз з умови
t2 – t1 = 2 c,
отримаємо систему трьох алгебраїчних
рівнянь з трьома невідомими h,
t1 і
t2
,
розв’язавши яку, знайдемо відповідь
задачі:







 .
.
Відповідь:
 .
.




 =1,5
м/с
=1,5
м/с =2,5
м/с
=2,5
м/с
 – ?
– ?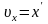 ;
;
 ;
;
 .
. ,
, .
. .
. .
. – прискорення
матеріальної точки.
– прискорення
матеріальної точки.