- •1. Место дисциплины в структуре ооп впо
- •2. Цели освоения дисциплины
- •3. Компетенции обучающегося, формируемые в результате освоения дисциплины (модуля)
- •Рабочая программа
- •Рабочая программа
- •Рабочая программа
- •Рабочая программа
- •5. Образовательные технологии
- •6. Учебно-методическое и информационное обеспечение дисциплины
- •7. Материально-техническое обеспечение дисциплины (модуля)
- •8. Методические рекомендации (материалы) для преподавателя
- •9. Методические указания для студентов
- •Темы лекционных занятий
- •Темы практических занятий Темы практических занятий
- •10. Учебно-методическое обеспечение самостоятельной работы студентов
- •11. Контрольно-оценочные материалы
- •Типовые задания для контрольных и самостоятельных работ.
- •Примерные контрольные работы Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа № 3
- •Примерные тестовые задания
- •Экзаменационные вопросы
- •Рейтинг-планы дисциплины по семестрам технологическая карта
- •Система оценивания
Примерные контрольные работы Контрольная работа №1
Вариант 1
1.![]() Найти
произведения матриц: а)
Найти
произведения матриц: а)
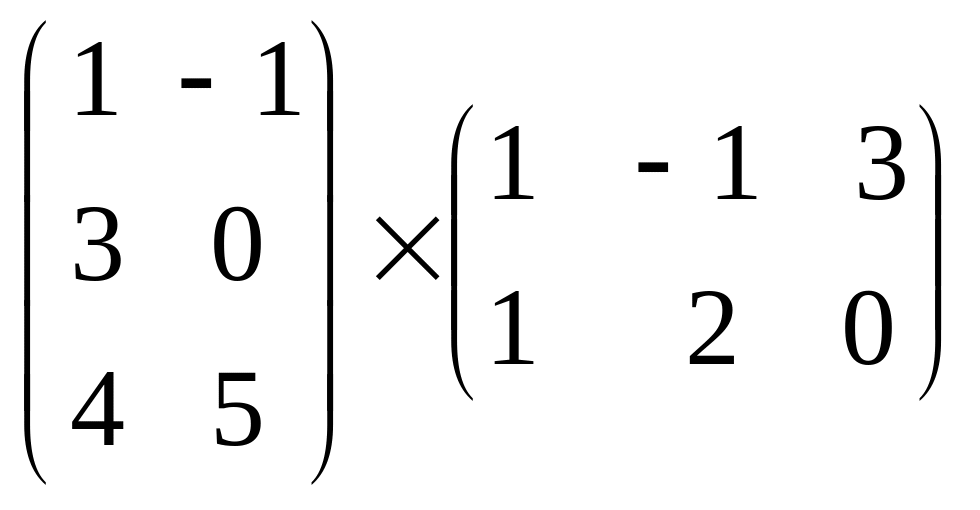 ;
б)
;
б)
![]()
![]()
2.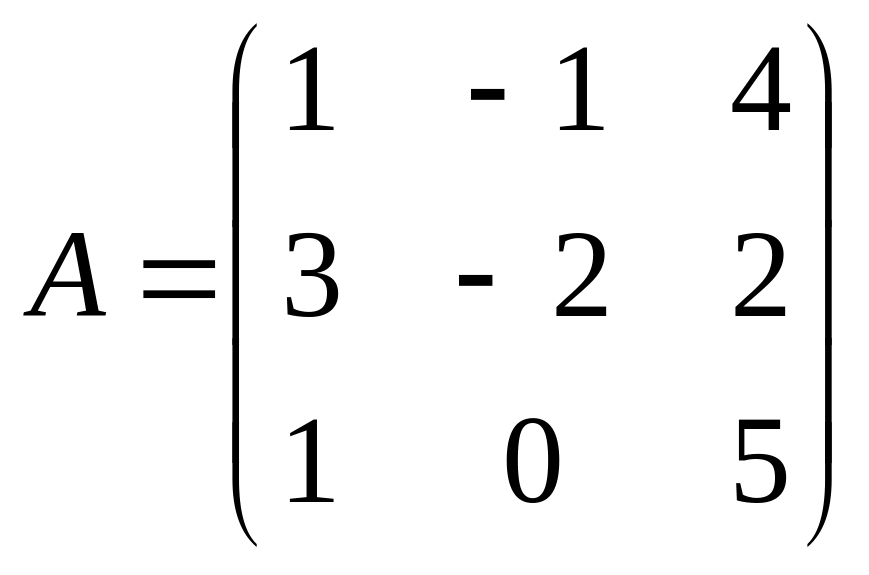 ;
;
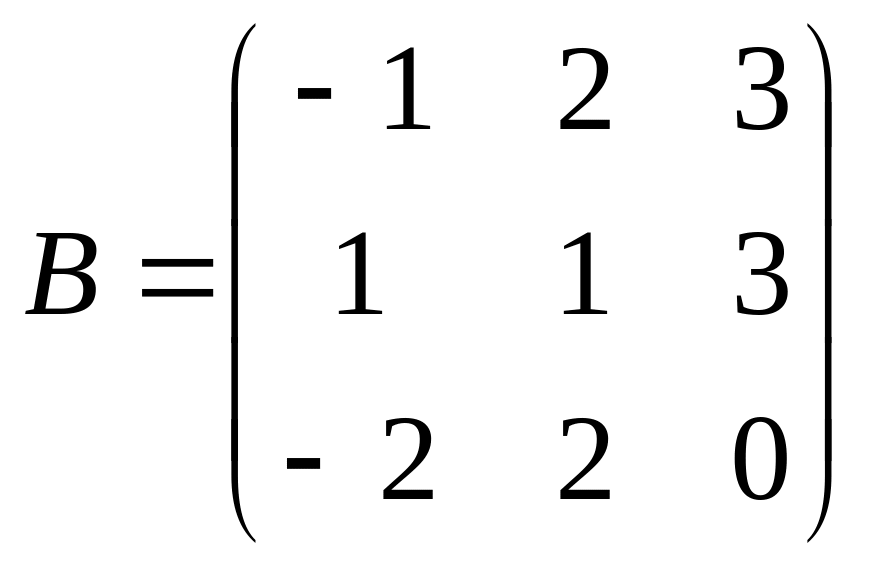 Найти:
Найти:
![]()
3.Найти матрицу,
обратную для матрицы: 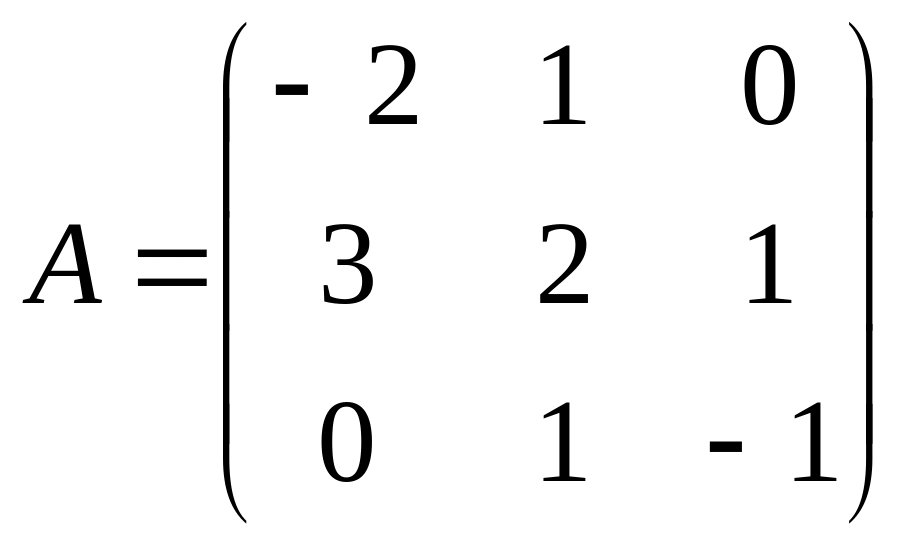
Вычислить определители: а)
 б)
б)
 в)
в)

Решить СЛУ методом Крамера
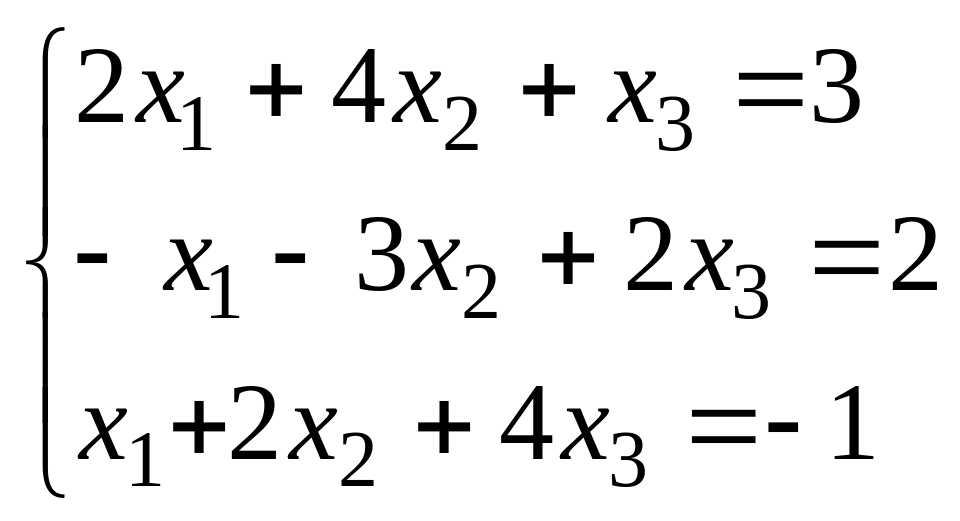
Решить СЛУ методом Гаусса: а)
 б)
б)
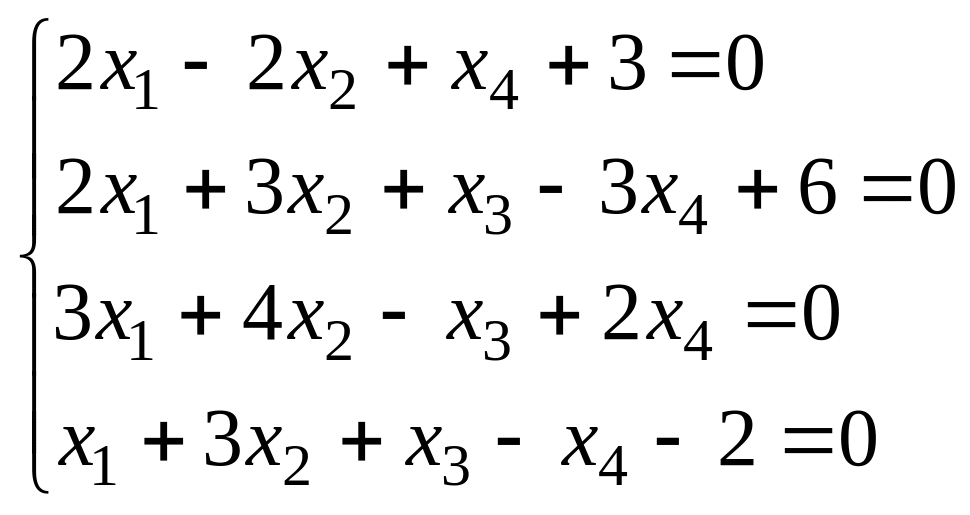
Найти ранг матрицы
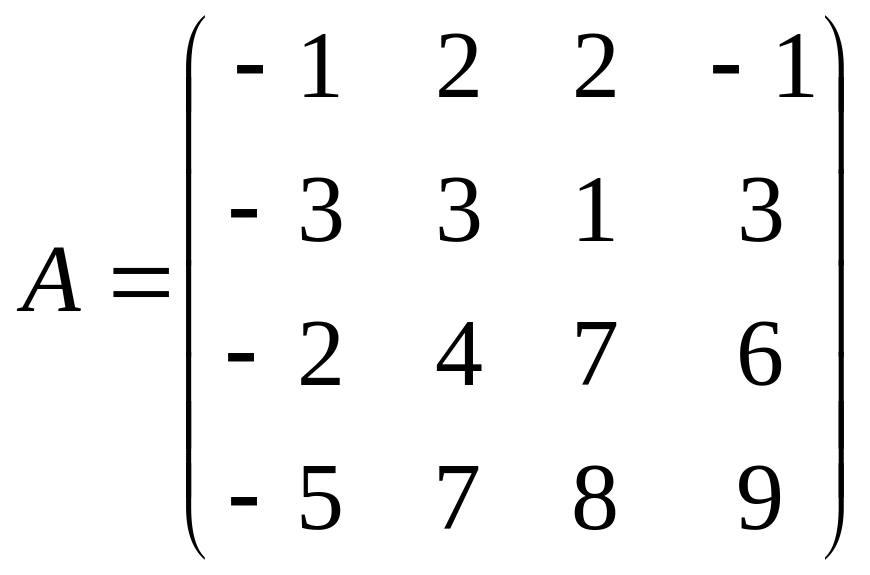
Вариант 3
1. Найти произведение
матриц: а)
 ;
б)
;
б)
![]()
![]()
 =
=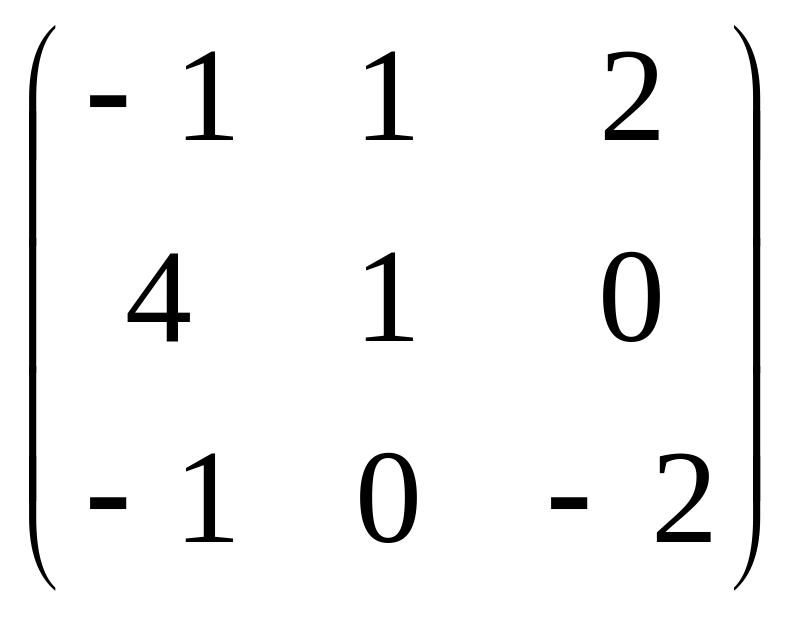 ;
;
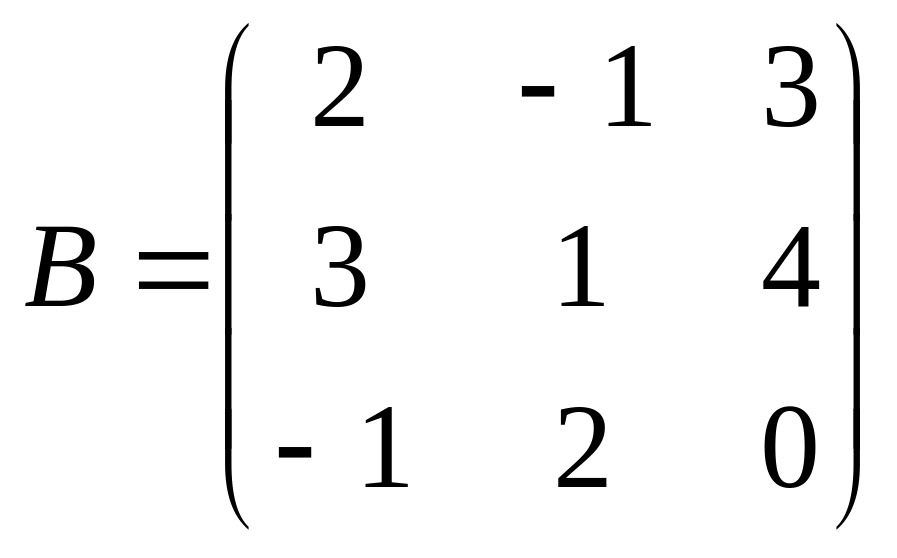 Найти:
Найти:
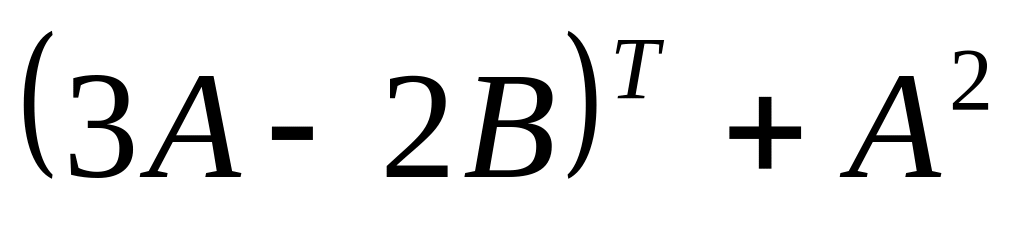
3.Найти матрицу,
обратную для матрицы: 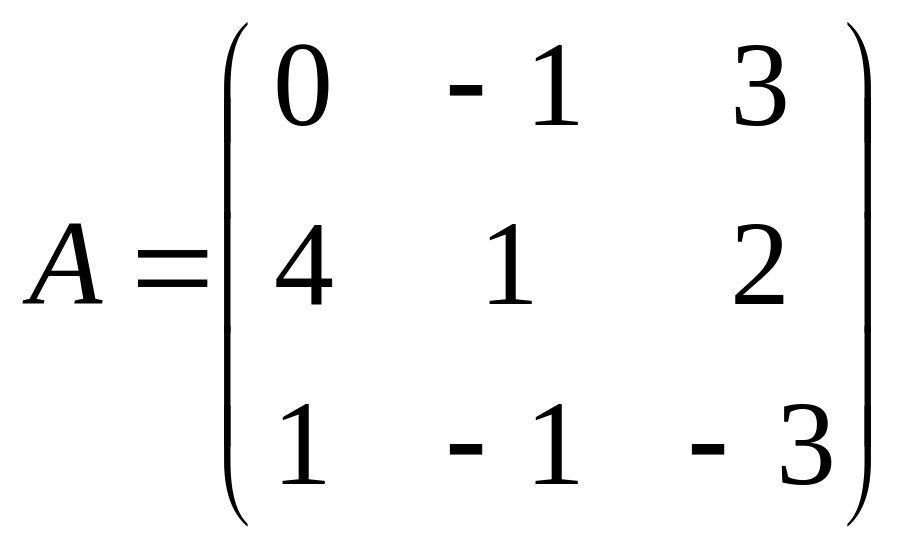
Вычислить определители: а)
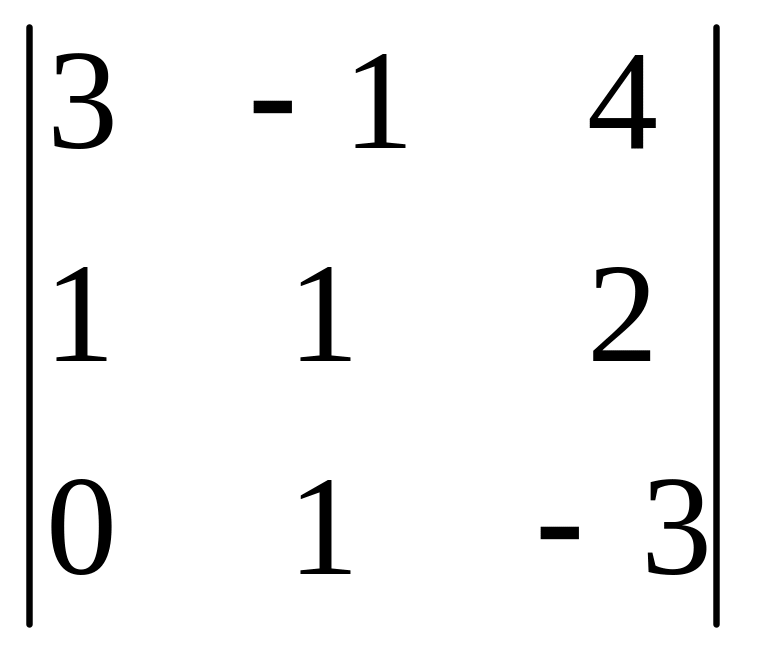 б)
б)
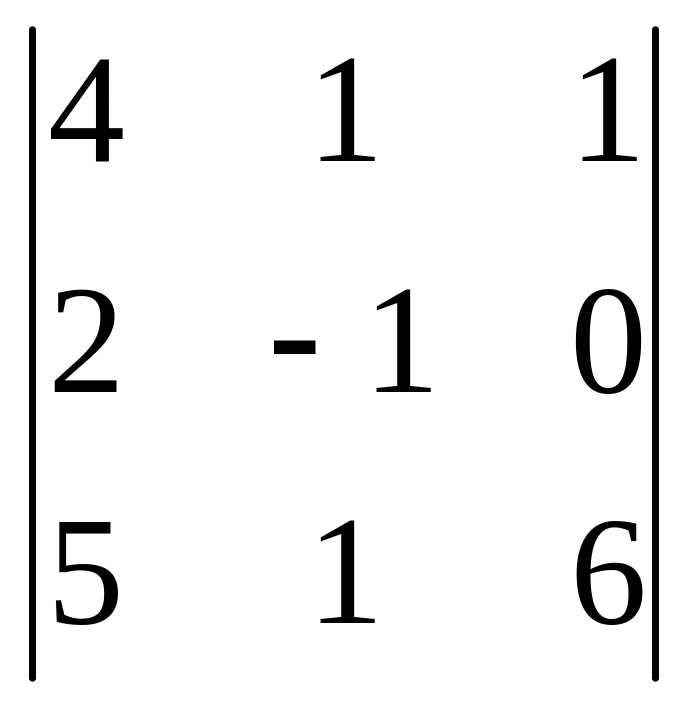 в)
в)
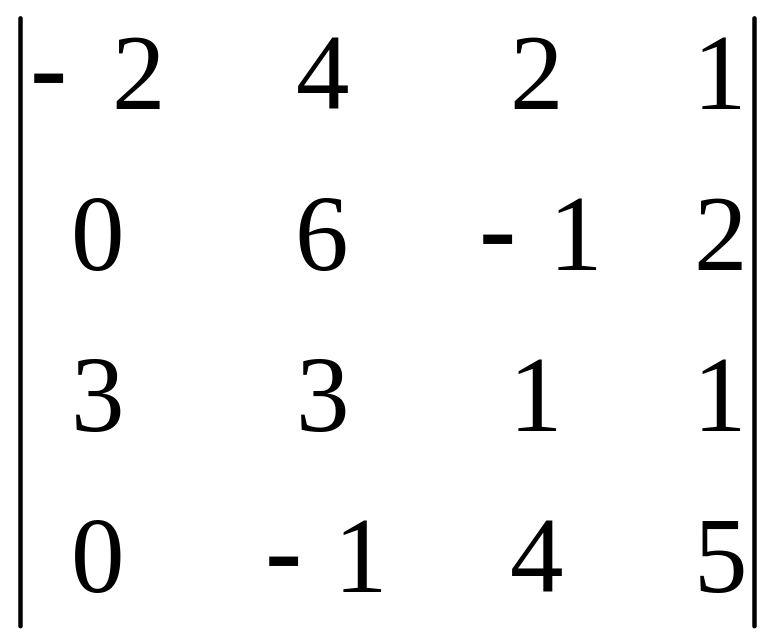
Решить СЛУ методом Крамера

Решить СЛУ методом Гаусса: а)
 б)
б)

Найти ранг матрицы

Вариант 2
1. Найти произведение
матриц: а)
![]() ;
б)
;
б)
![]()
![]()
2.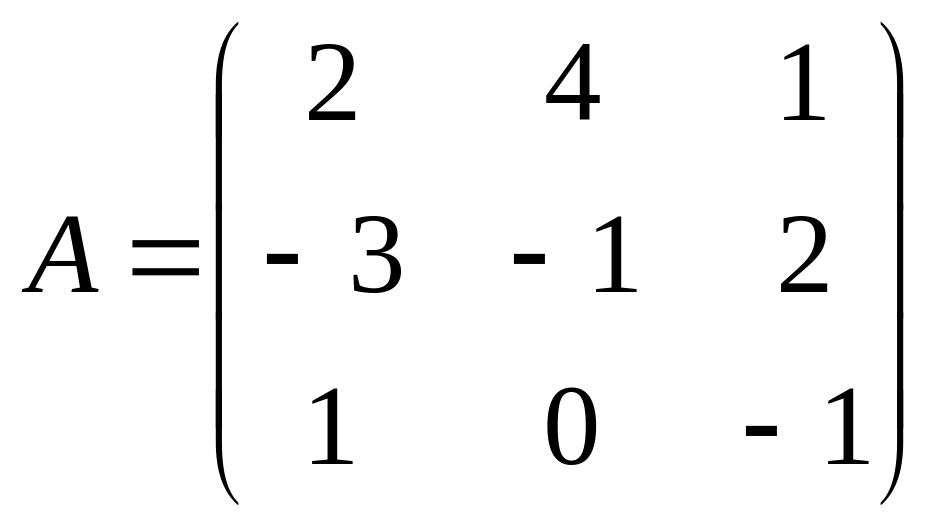 ;
;
 Найти:
Найти:
![]()
3.Найти матрицу,
обратную для матрицы: 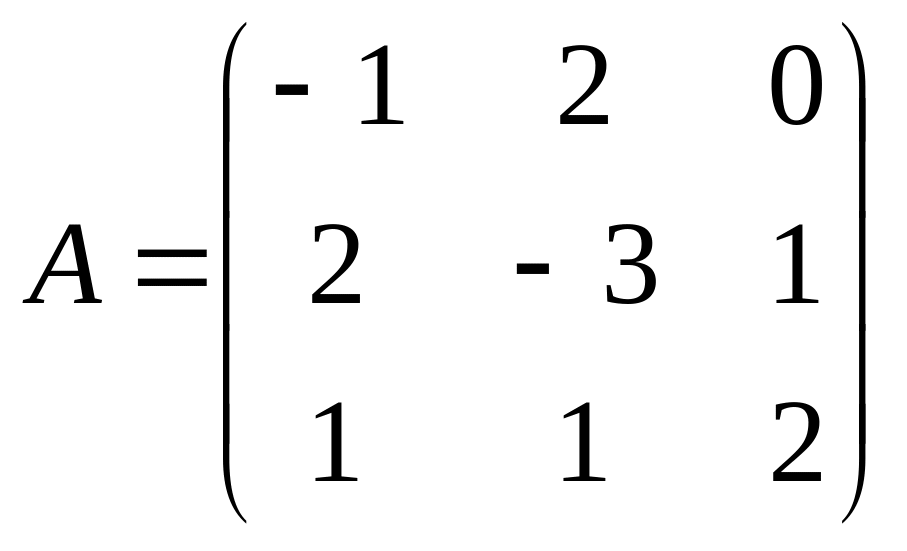
Вычислить определители: а)
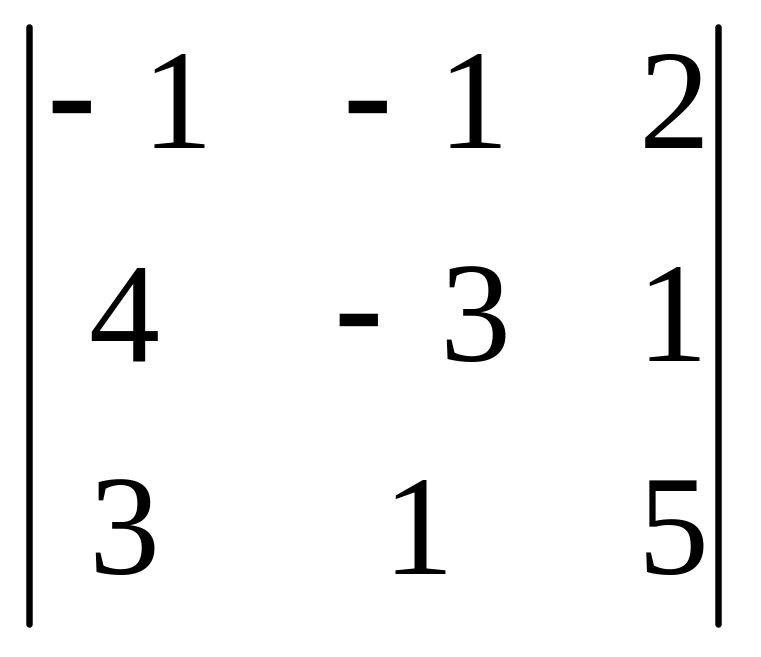 б)
б)
 в)
в)

Решить СЛУ методом Крамера
Решить СЛУ методом Гаусса: а)
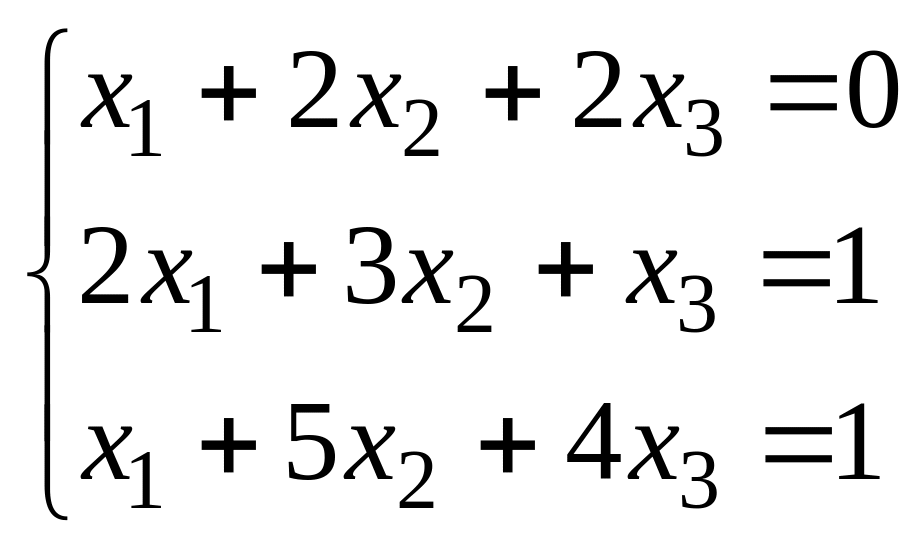 б)
б)
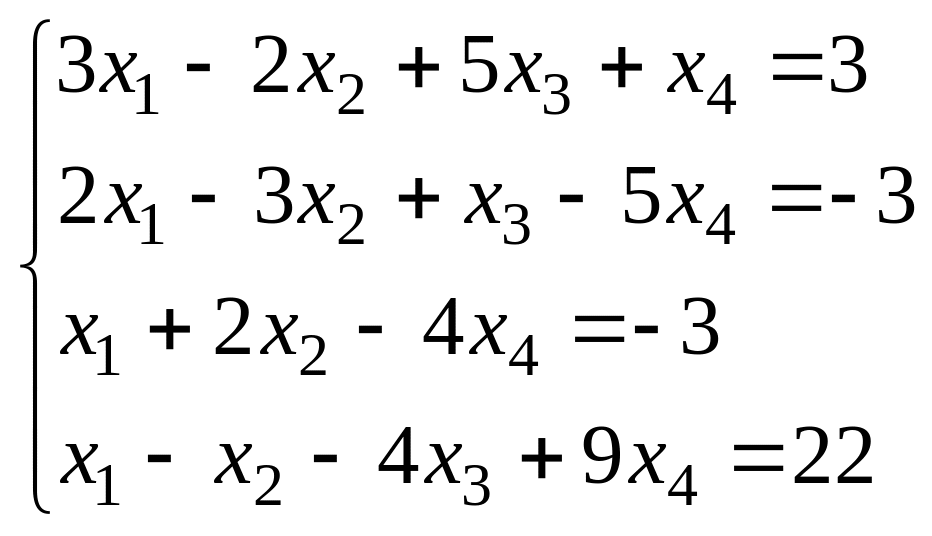
Найти ранг матрицы
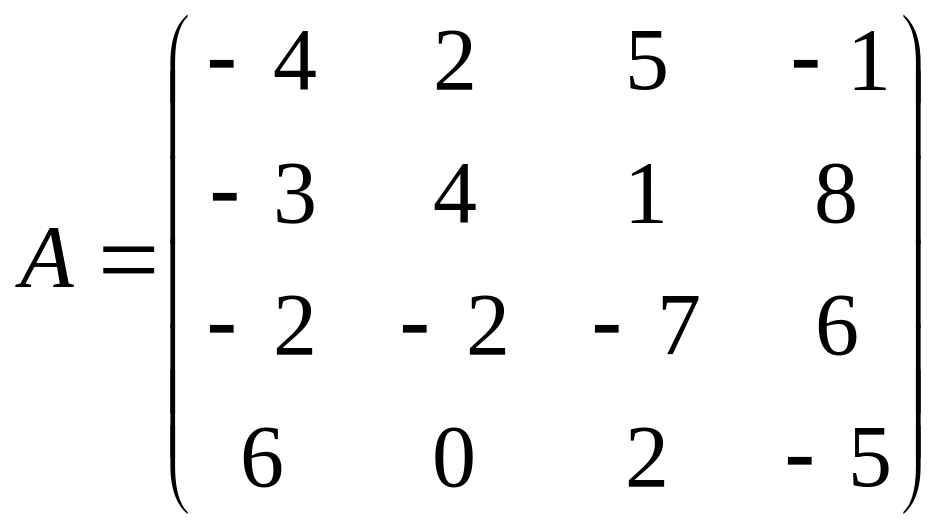
Вариант 4
1. Найти произведение
матриц: а)
![]() ;
б)
;
б)
![]()
![]()
2. ;
;
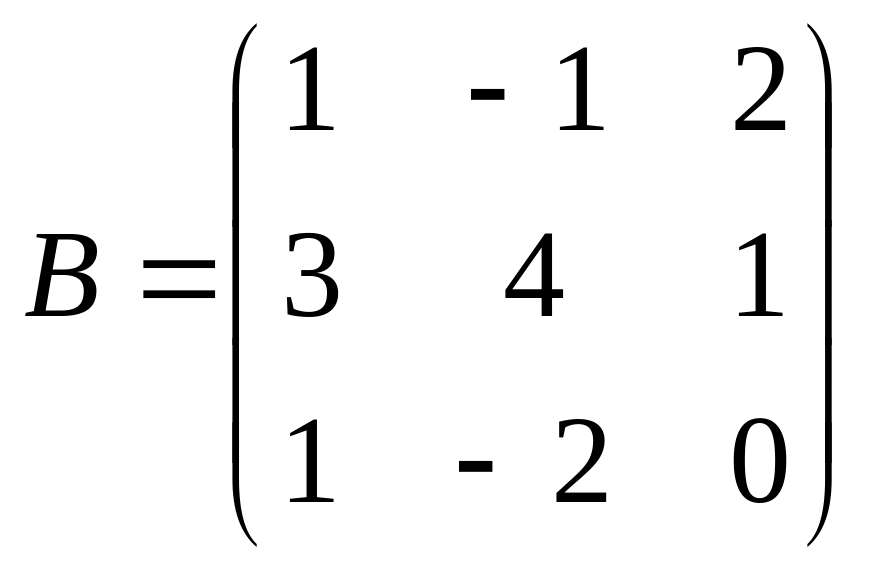 Найти:
Найти:
![]()
3.Найти матрицу,
обратную для матрицы: 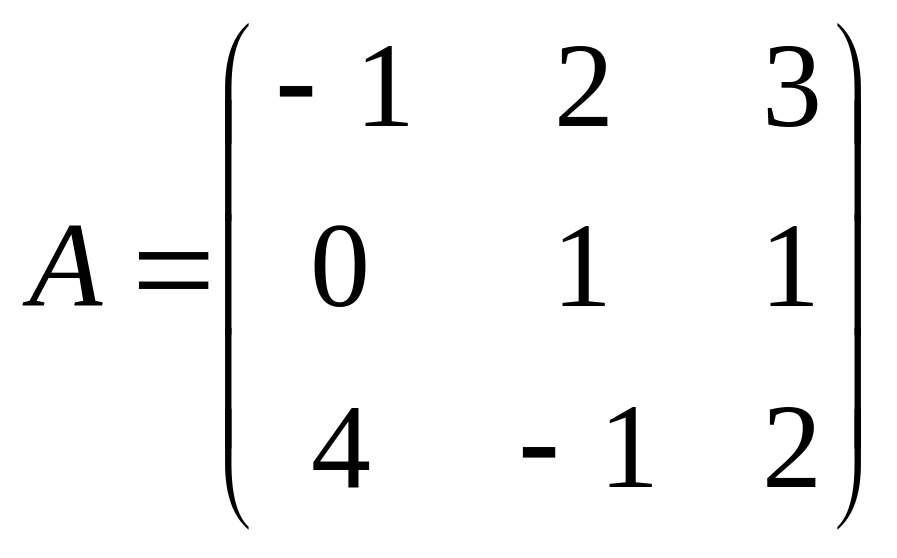
4.Вычислить
определители: а)
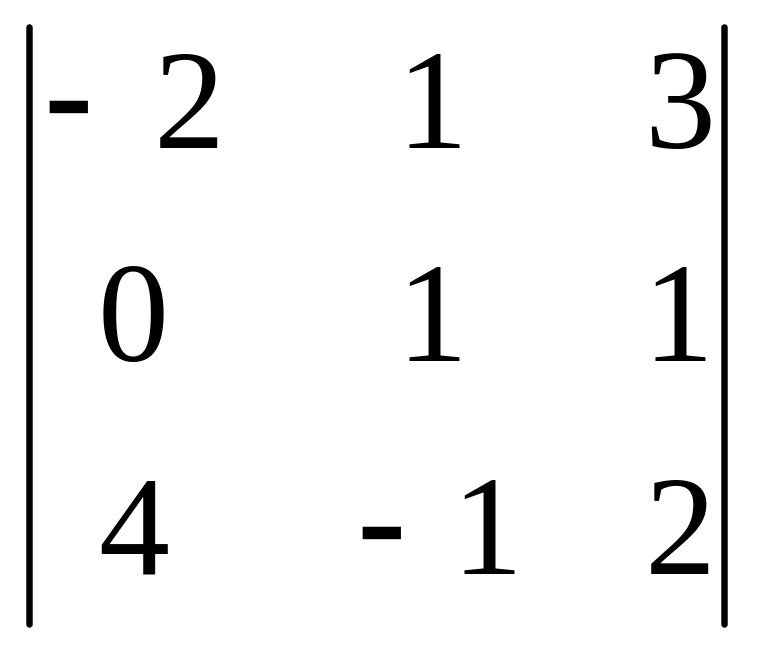 б)
б)
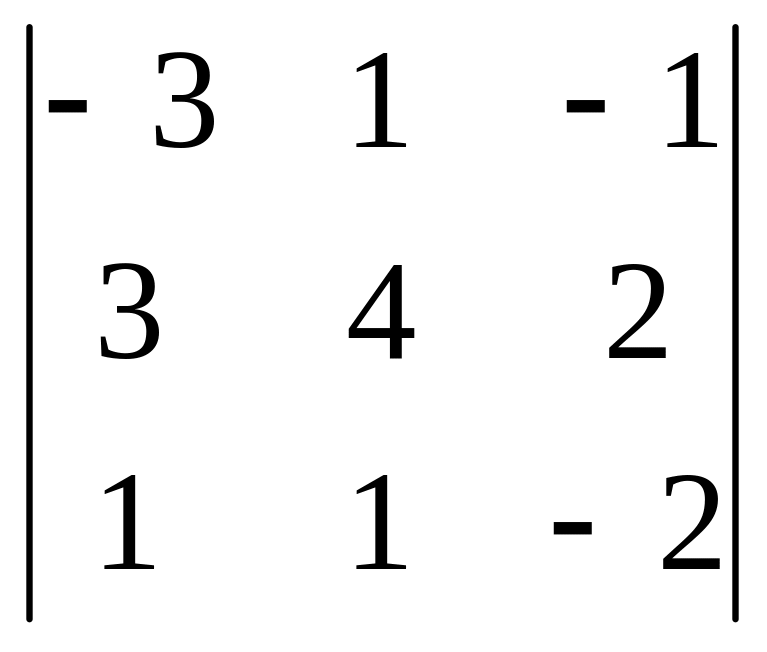 в)
в)
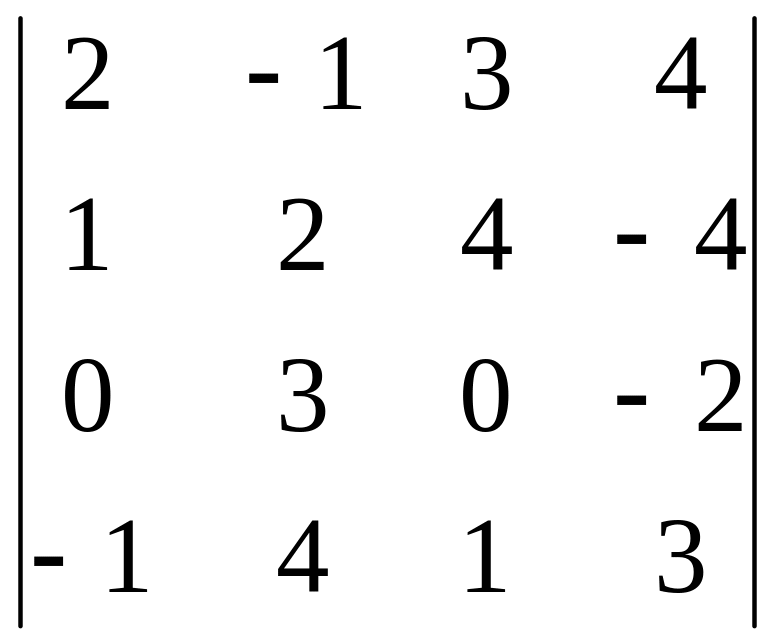
5.Решить СЛУ методом
Крамера
![]()
6.Решить СЛУ методом
Гаусса: а)
![]() б)
б)
![]()
7. Найти ранг матрицы
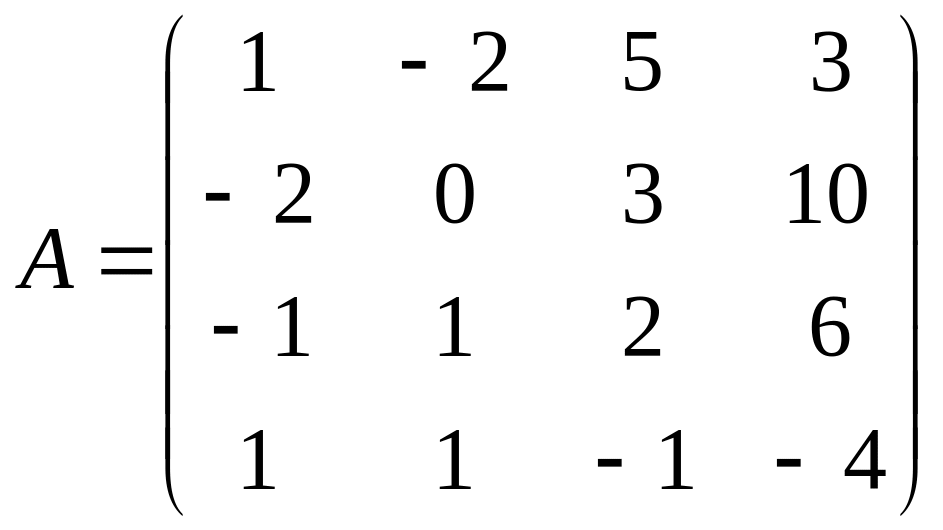
Контрольная работа №2
Вариант 1
Определить, есть ли тупой угол среди внутренних углов треугольника АВС, если А(4,-1,4), В(0,7,-4) и С(3,1,-2).
Даны точки А(-1,5,-10), В(5, -7,8), С (2,2,-7), D (5,-4,2). Проверить, что векторы АВ и СD коллинеарные, установить какой из них длиннее другого и во сколько раз, как они направлены – в одну или в противоположные стороны.
Векторы
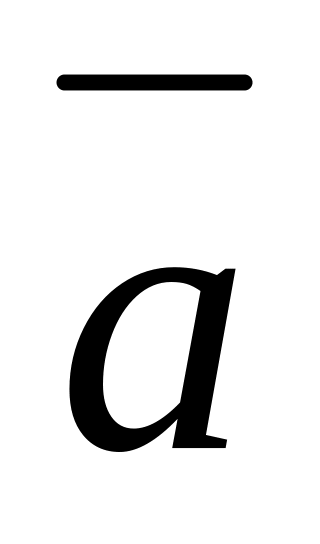 и
и
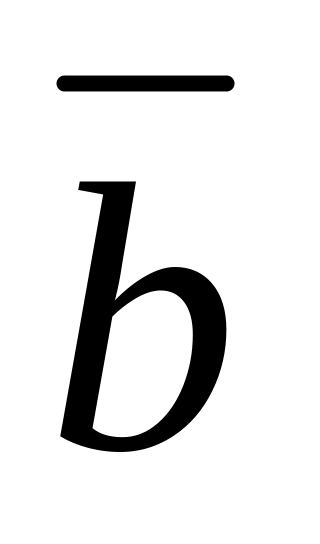 взаимно
перпендикулярны, вектор
взаимно
перпендикулярны, вектор
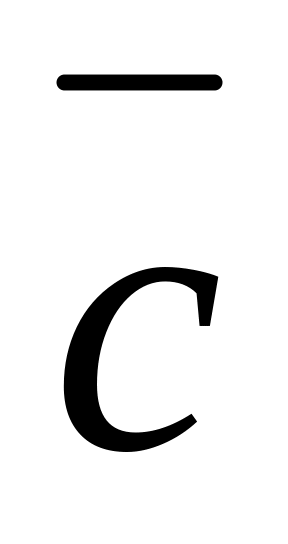 образует
с ними углы, равные
образует
с ними углы, равные

 .
Зная, что
.
Зная, что
 ,
вычислить
,
вычислить
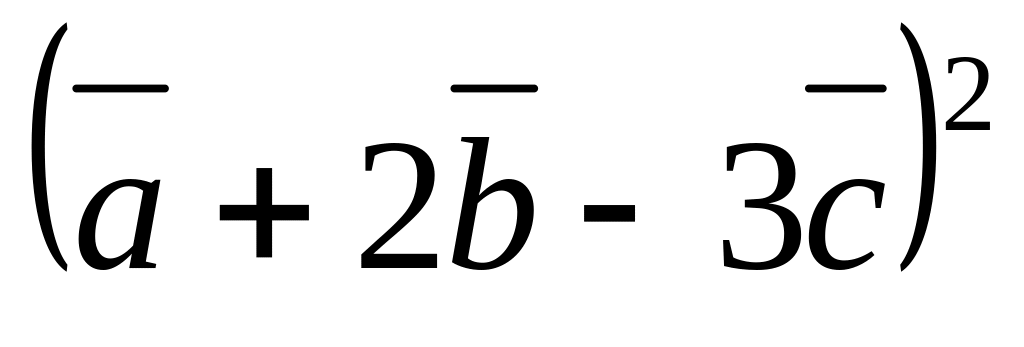 .
.Даны вершины треугольника А(1,-1,2), В(5,-6,2) и С(1,3,-1). Вычислить длину его высоты, опущенной из вершины В на сторону АС.
Проверить компланарность векторов (2,-1,3),
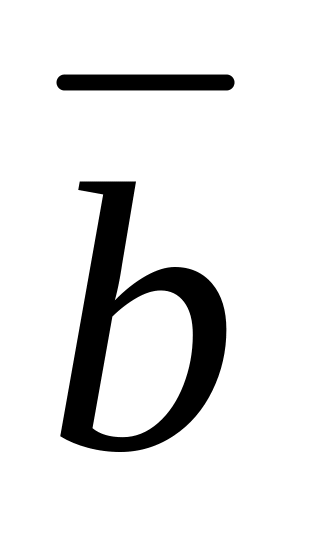 (1,0,-1),
(2,4,1).
(1,0,-1),
(2,4,1).На плоскости даны два вектора
 (1,
-3) и
(1,
-3) и
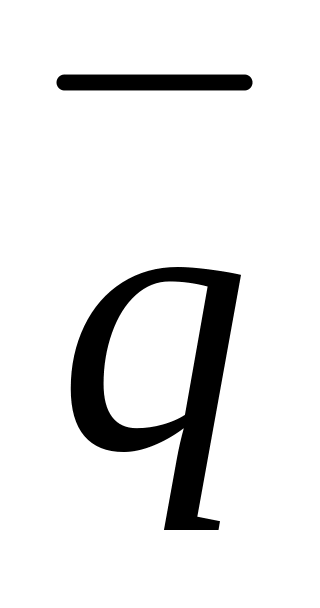 (2,
-5). Найти разложение
(6,1)
по базису
,
.
(2,
-5). Найти разложение
(6,1)
по базису
,
.
Вариант 2
Доказать, что внутренние углы треугольника АВС, где А(3,-2,5), В(-2,1,-3), С(5,1,-1), острые.
Даны точки А(1,-1,4), В(-2, 11,-2), С (4,0,-7), D (5,-4,-5). Проверить, что векторы АВ и СD коллинеарные, установить какой из них длиннее другого и во сколько раз, как они направлены – в одну или в противоположные стороны.
Векторы и взаимно перпендикулярны, вектор образует с ними углы, равные . Зная, что , вычислить
 .
.Даны вершины треугольника А(1,2,0), В(3,0,-3) и С(5,2,6). Вычислить длину его высоты, опущенной из вершины А на сторону ВС.
Проверить компланарность векторов (3,-1,4), (1,1,2), (0,1,-3).
На плоскости даны два вектора (2, -4) и (3, 4). Найти разложение (2,5) по базису , .
Контрольная работа № 3
Вариант 1
Доказать, что треугольник с вершинами
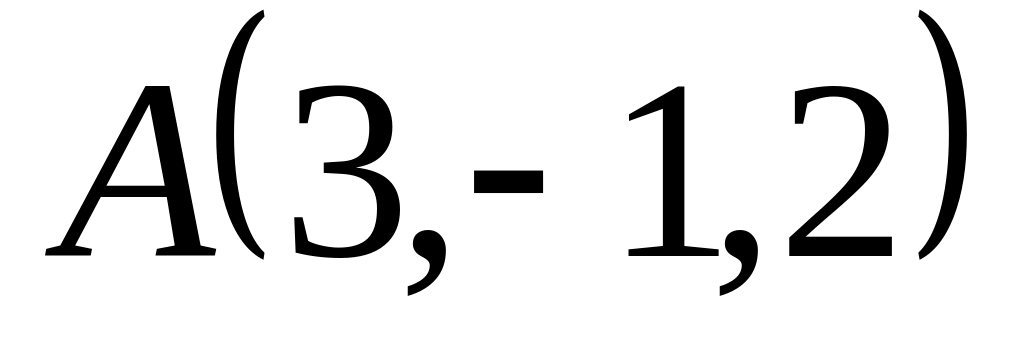 ,
,
 и
и
 равнобедренный.
равнобедренный.Проверить коллинеарность векторов
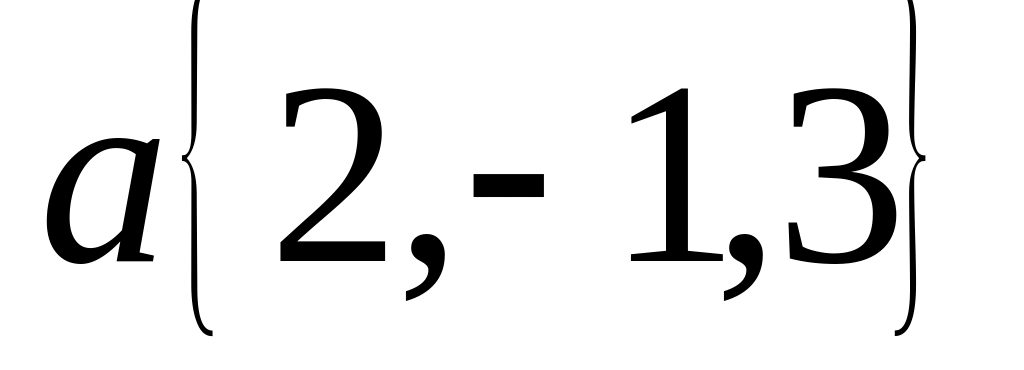 и
и
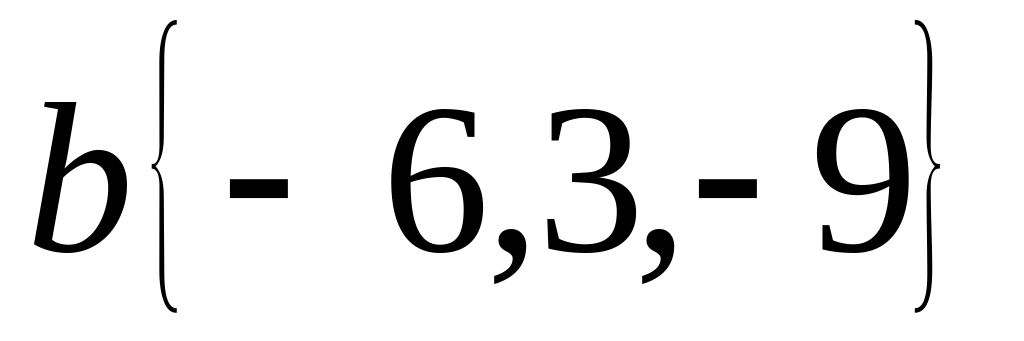 .
Установить какой из них длиннее другого
и во сколько раз, как они направлены –
в одну или в противоположные стороны.
.
Установить какой из них длиннее другого
и во сколько раз, как они направлены –
в одну или в противоположные стороны.Векторы
 и
и
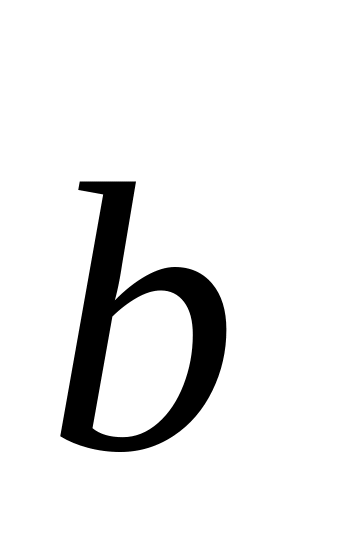 взаимно перпендикулярны; вектор
взаимно перпендикулярны; вектор
 образует с ними углы, равные
;
зная, что
образует с ними углы, равные
;
зная, что
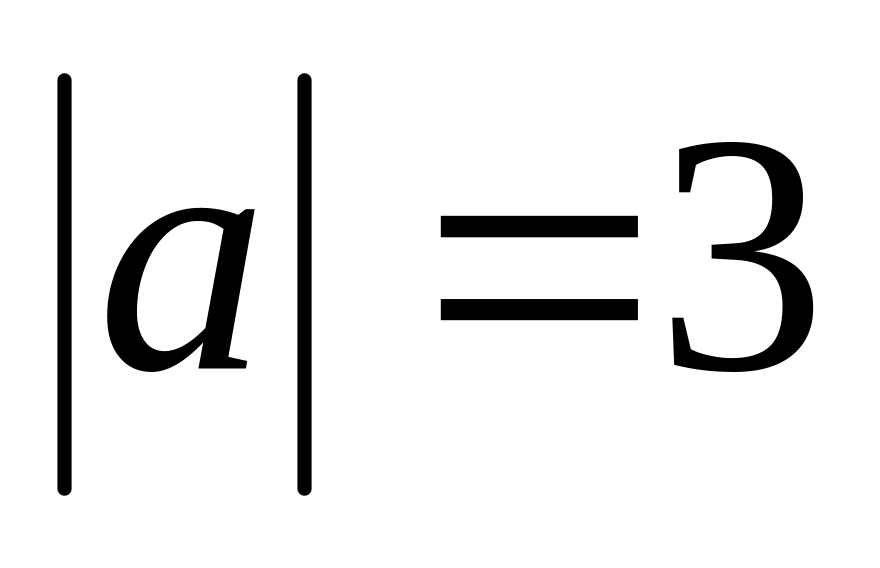 ,
,
 |,
|,
 ,
вычислить
,
вычислить
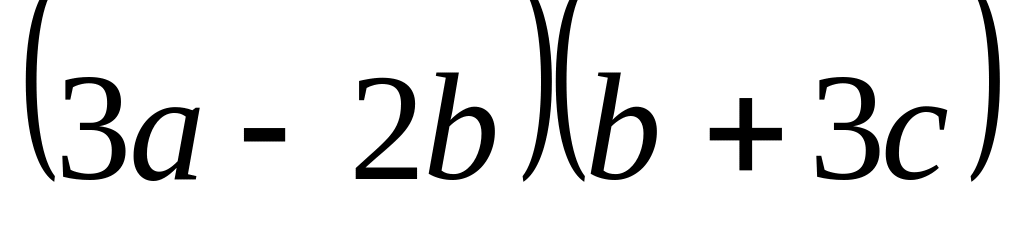 .
.Векторы , , образующие правую тройку, взаимно перпендикулярны. Зная, что
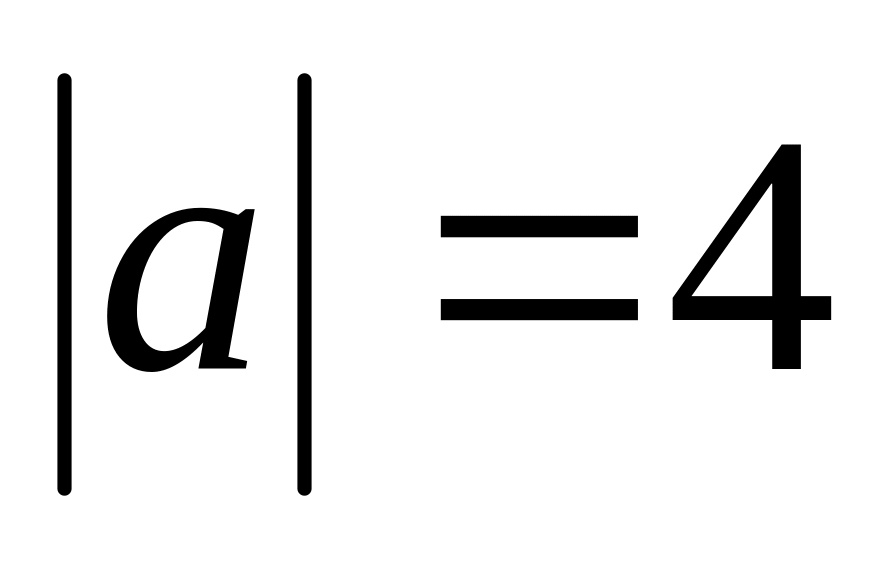 ,
,
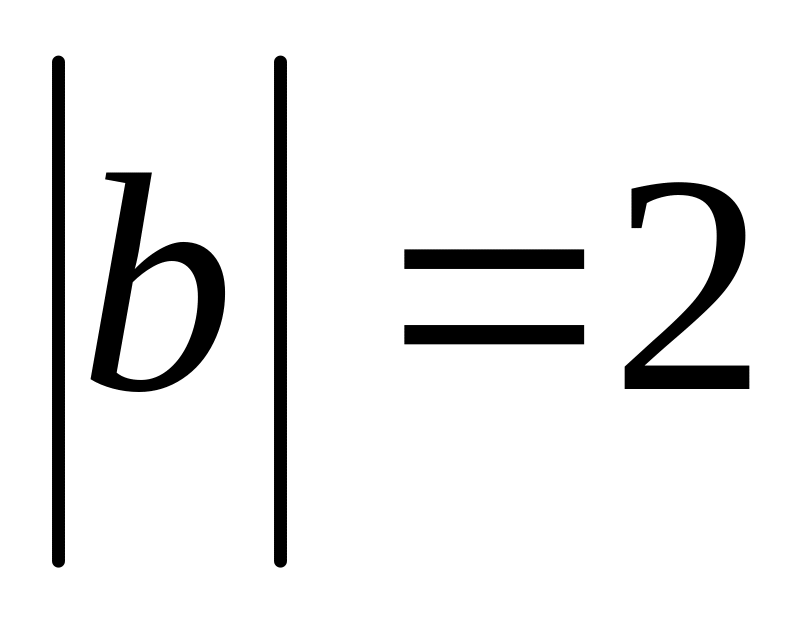 ,
,
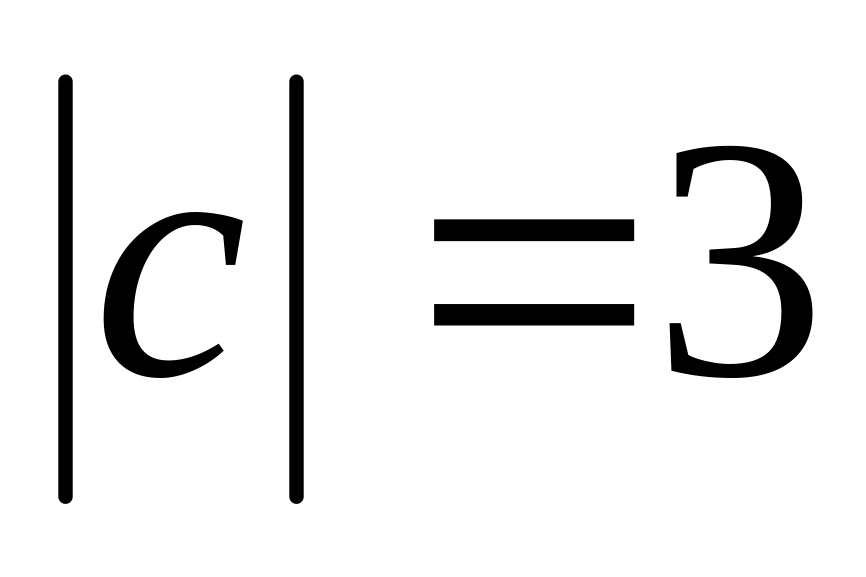 ,
вычислить
,
вычислить
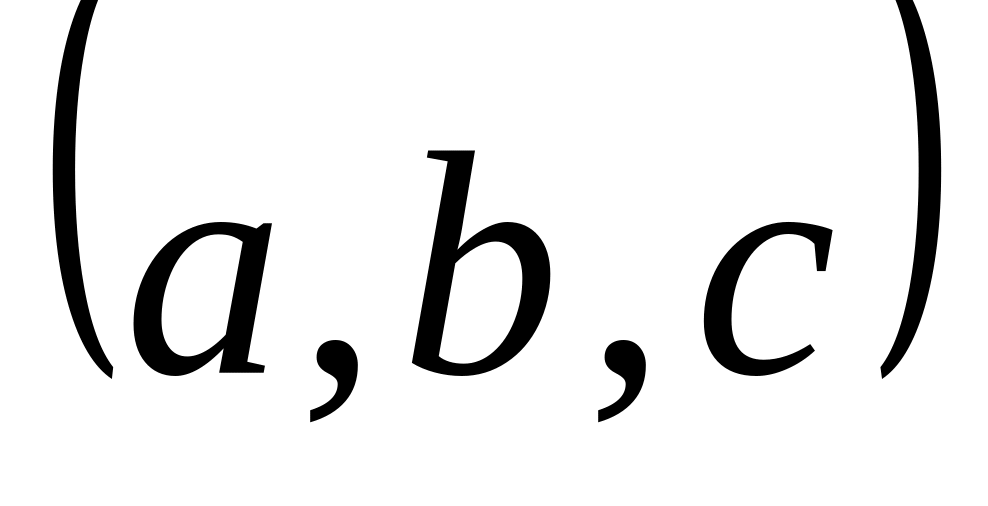 .
.Вычислить эксцентриситет эллипса, если расстояние от фокуса до дальней вершины большой оси в 1,5 раза больше расстояния до вершины малой оси.
В данной системе координат гипербола имеет каноническое уравнение. Составить это уравнение, если длина мнимой полуоси равна 1, а вершина гиперболы делит отрезок между фокусами в отношении 4:1.
Составить уравнение параболы, если ось параболы параллельна оси Oy, фокус лежит на оси Ox, парабола проходит через начало координат и высекает на оси Ox отрезок длины 6.
Составить уравнение касательной к кривой
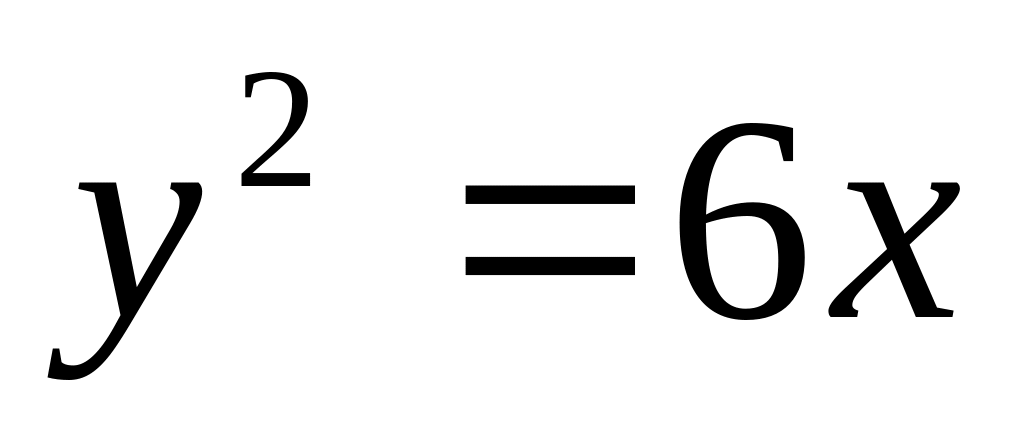 в точке
в точке
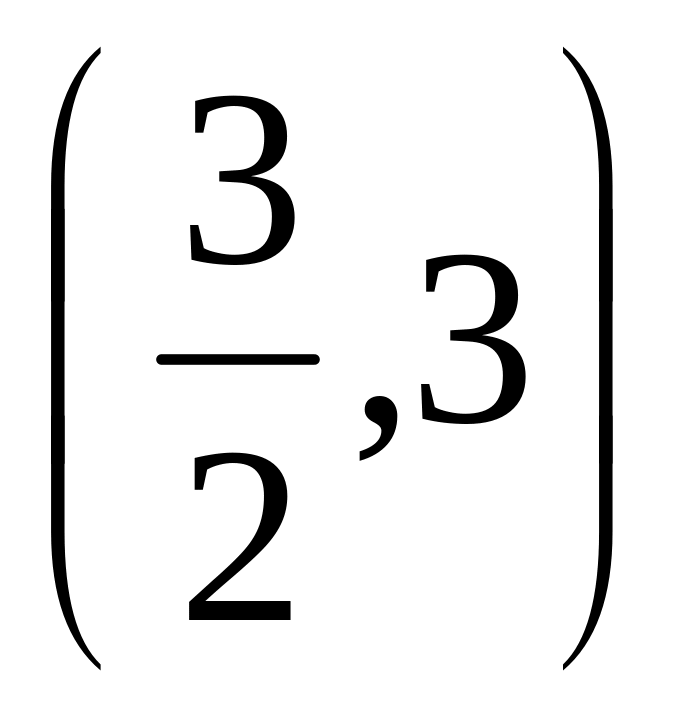 .
.
Вариант 2
Доказать, что треугольник с вершинами
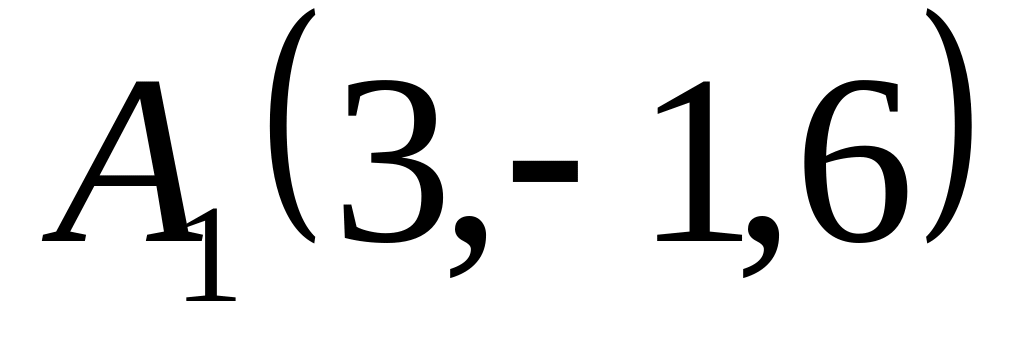 ,
,
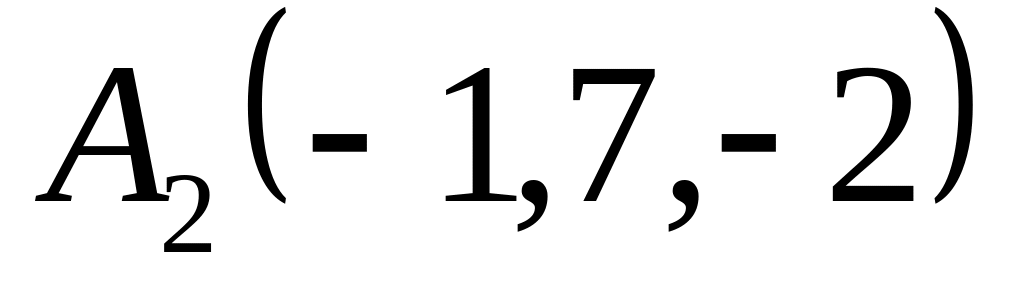 ,
,
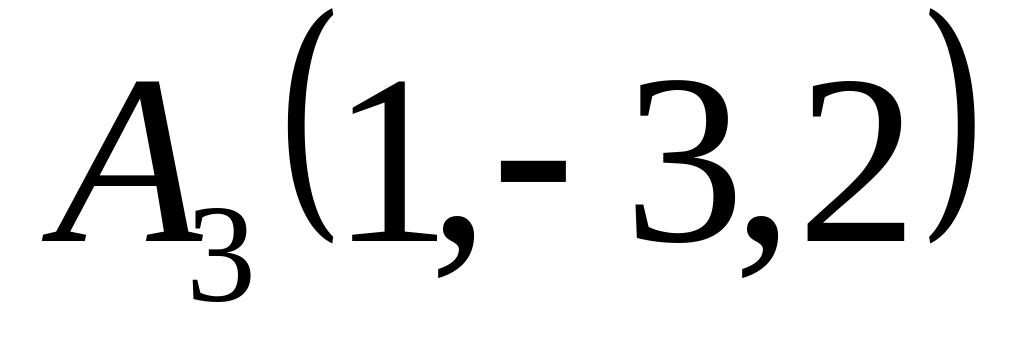 прямоугольный.
прямоугольный.
Определить, при каких значениях
 ,
,
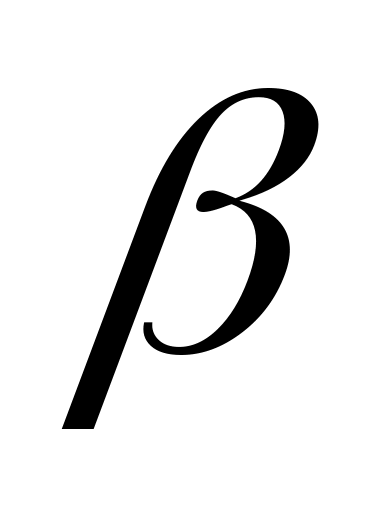 векторы
векторы
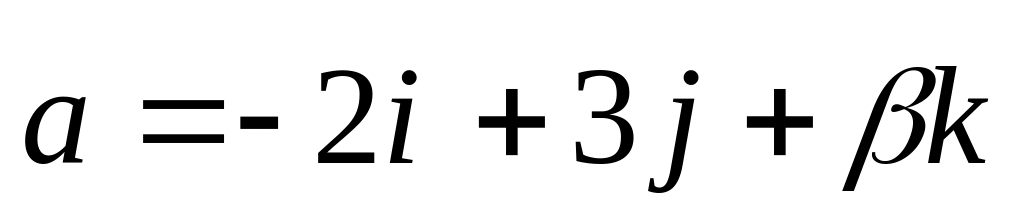 и
и
 коллинеарные.
коллинеарные.Векторы и взаимно перпендикулярны; вектор образует с ними углы, равные ; зная, что , |, , вычислить
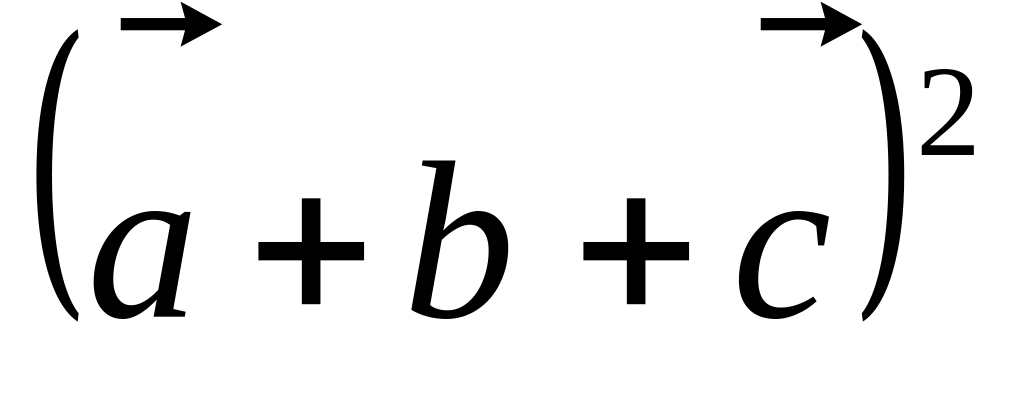 .
.Вектор перпендикулярен к векторам и , угол между и равен 300 . Зная, что
 ,
,
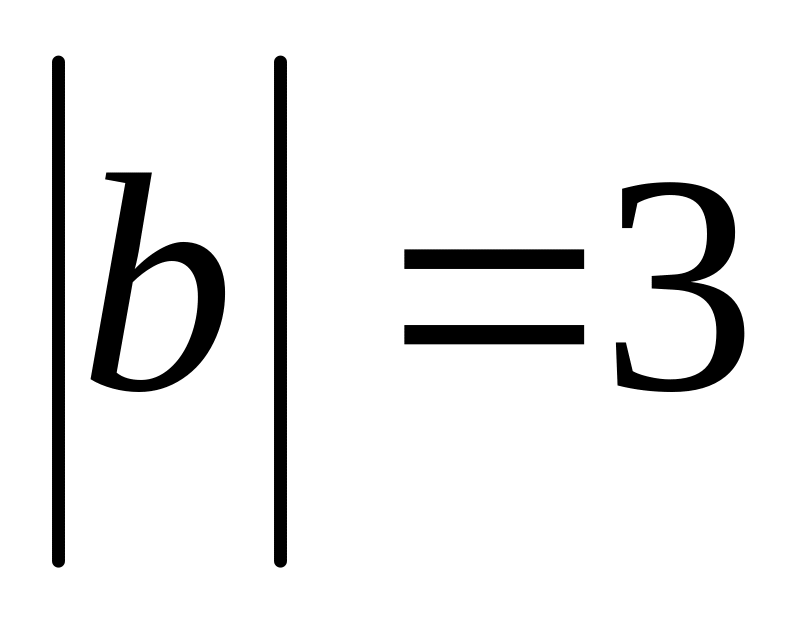 ,
,
вычислить
.
,
,
вычислить
.Вычислить эксцентриситет гиперболы, имеющей в данной системе координат каноническое уравнение, если расстояние от точки M(5,-4), принадлежащей гиперболе, до директрис относятся как 2:1.
Составить уравнение эллипса, если точки F1(5,1) и F2(-1,1) являются фокусами а прямая
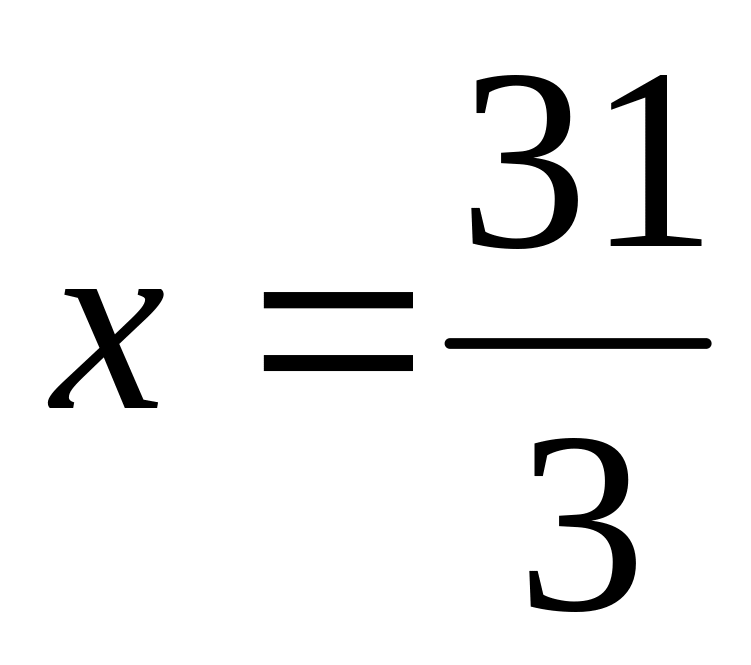 - одной из директрис.
- одной из директрис.В данной системе координат парабола имеет каноническое уравнение. Составить это уравнение, если расстояние от фокуса до директрисы равно 12.
Проверить, что прямая
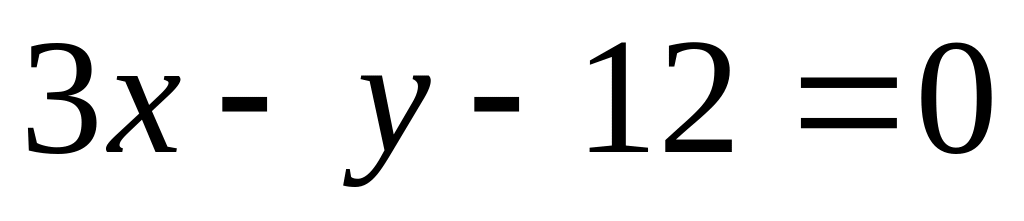 касается кривой
касается кривой
 ,
и найти координаты точки касания.
,
и найти координаты точки касания.
Вариант 3
Определить, есть ли тупой угол среди внутренних углов треугольника
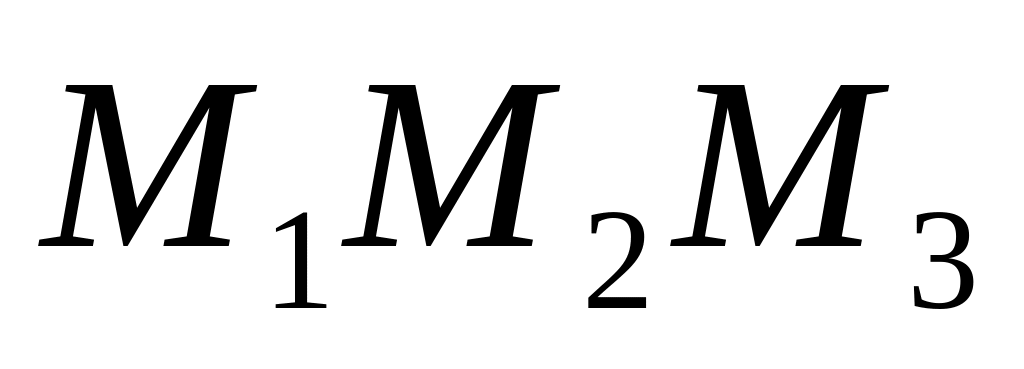 ,
где
,
где
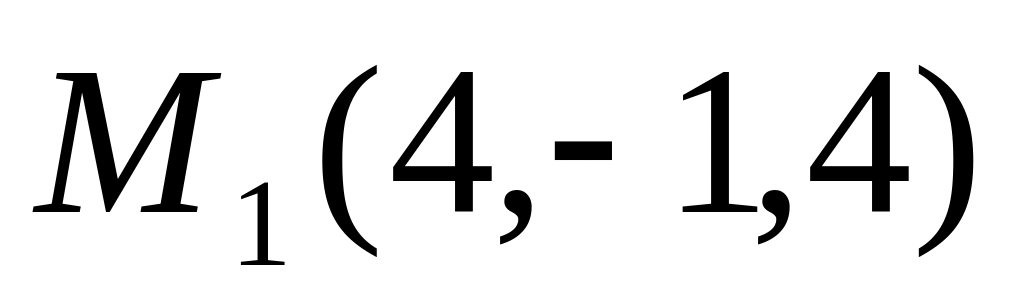 ,
,
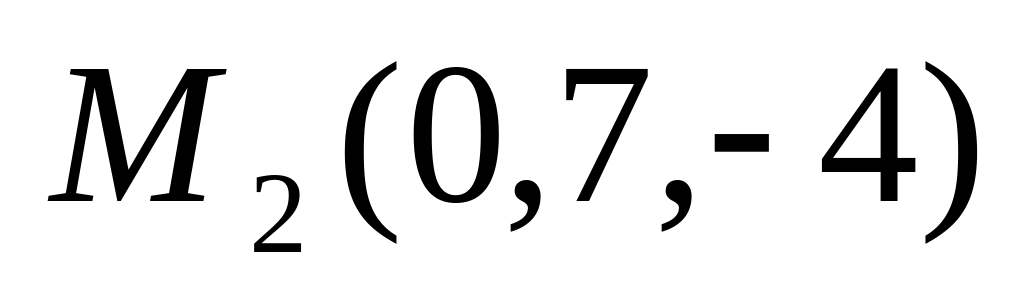 ,
,

Проверить, что четыре точки
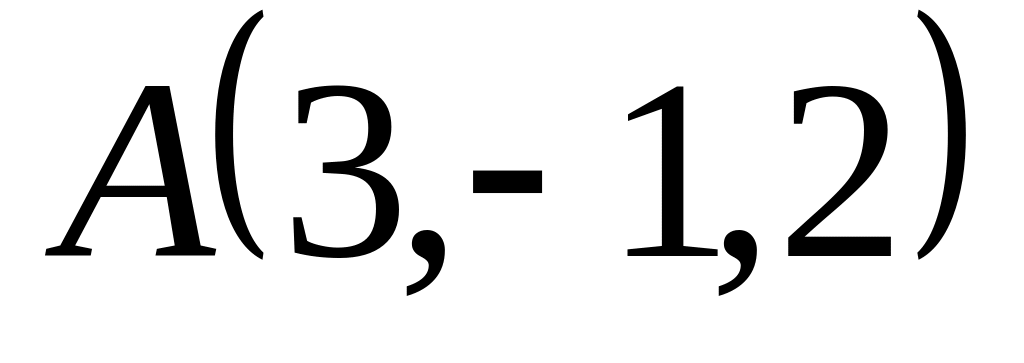 ,
,
 ,
,
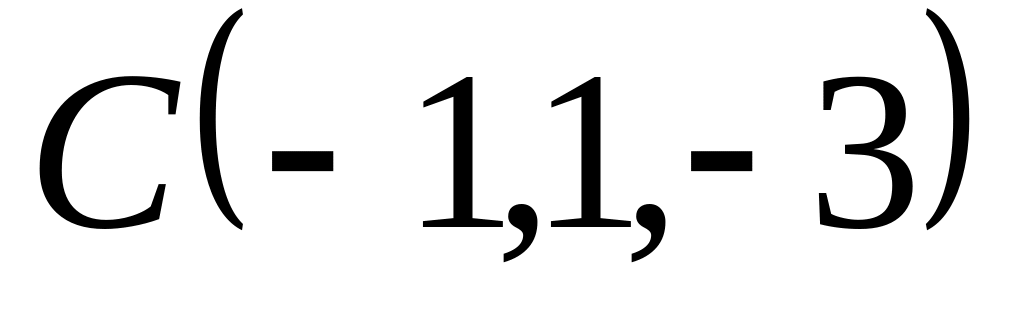 ,
,
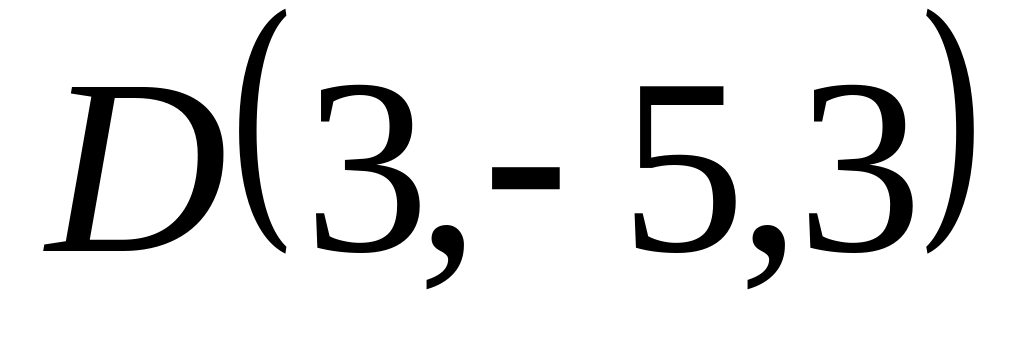 служат вершинами трапеции.
служат вершинами трапеции.Векторы и взаимно перпендикулярны; вектор образует с ними углы, равные ; зная, что , , , вычислить
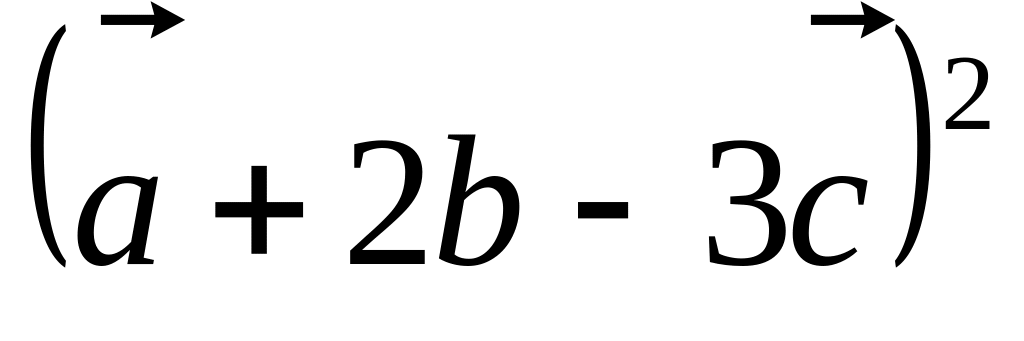 .
.Даны точки
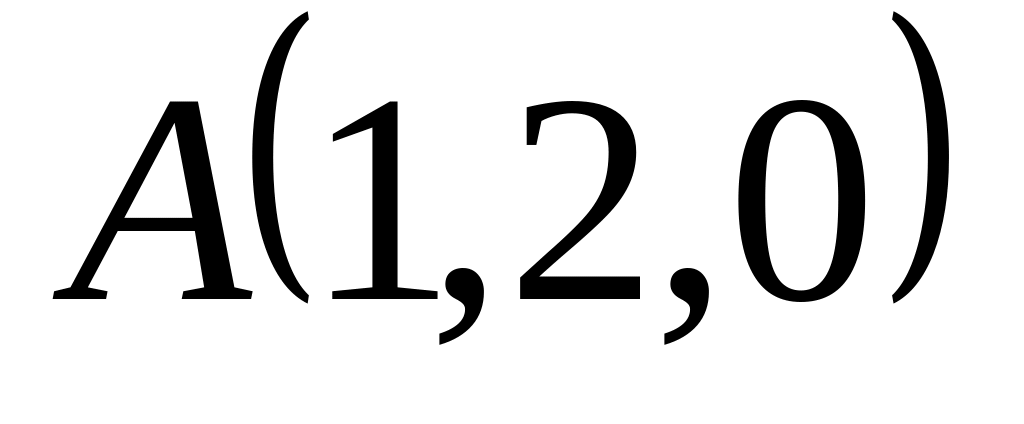 ,
,
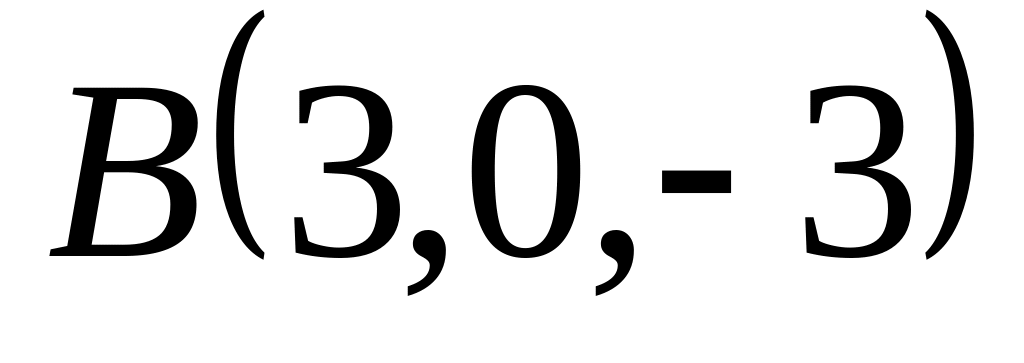 и
и
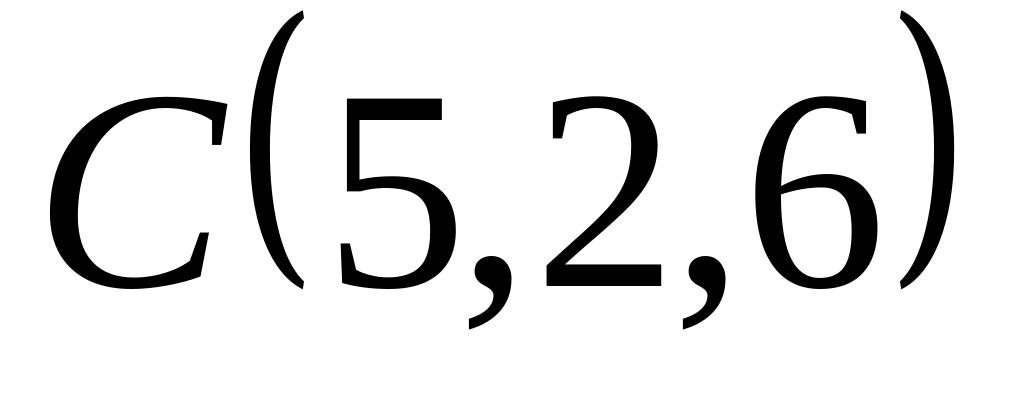 .
Вычислить площадь треугольника
.
Вычислить площадь треугольника
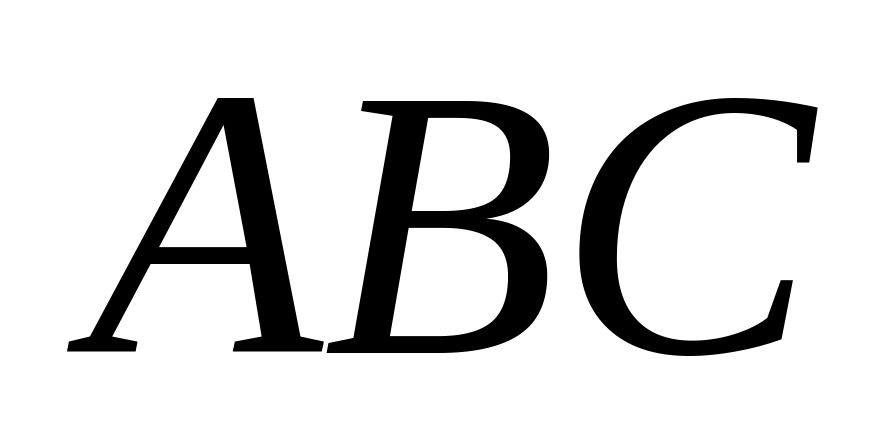 .
.
Вариант 4
Доказать, что внутренние углы треугольника
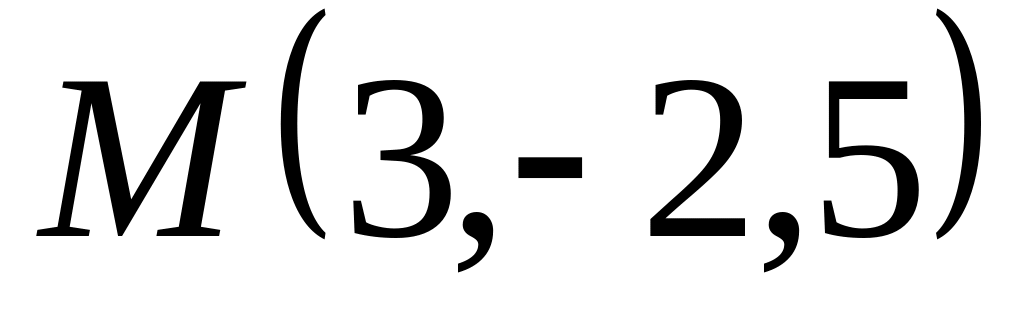 ,
,
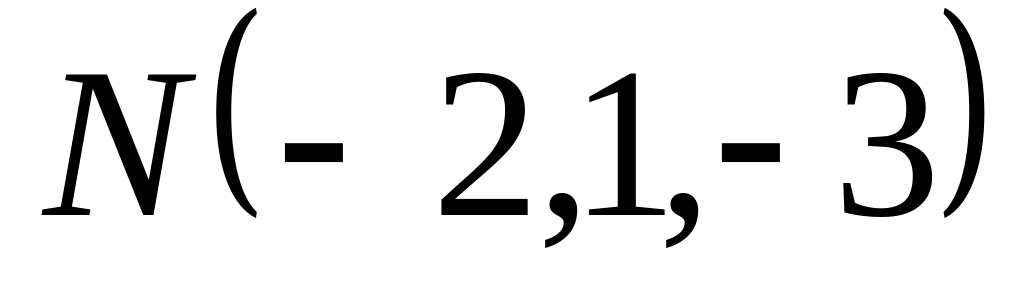 ,
,
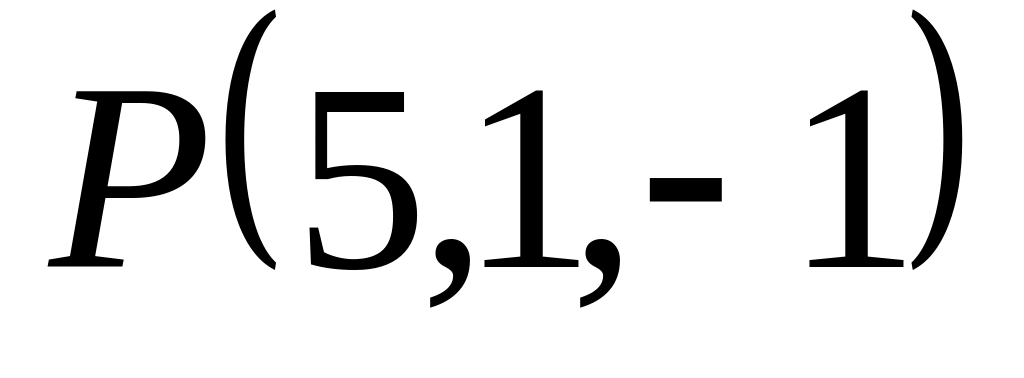 острые.
острые.Даны точки
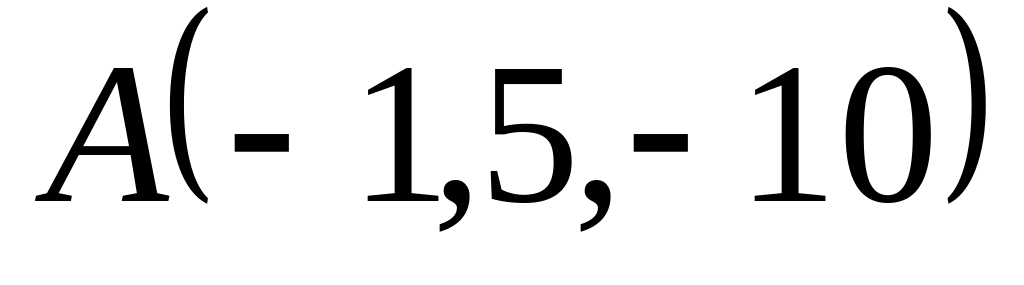 ,
,
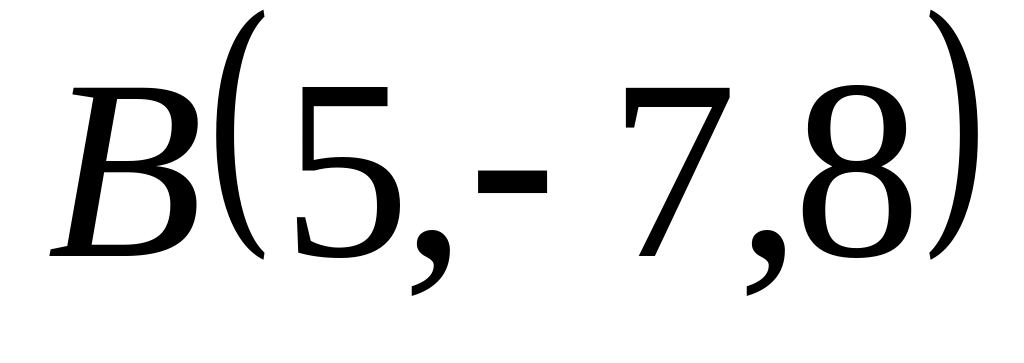 ,
,
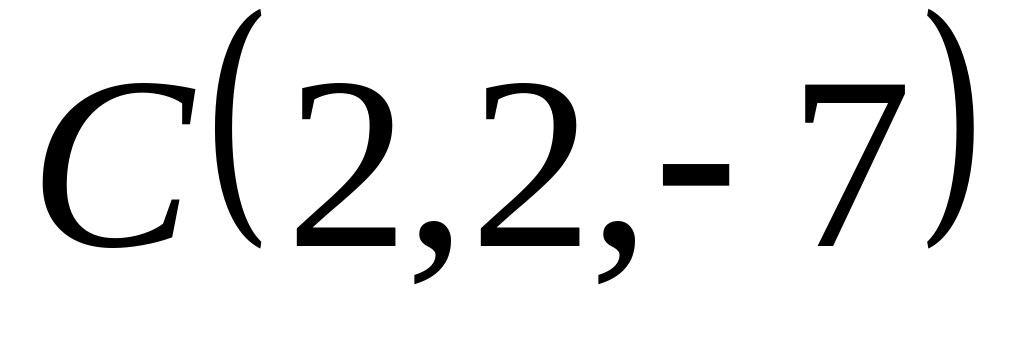 и
и
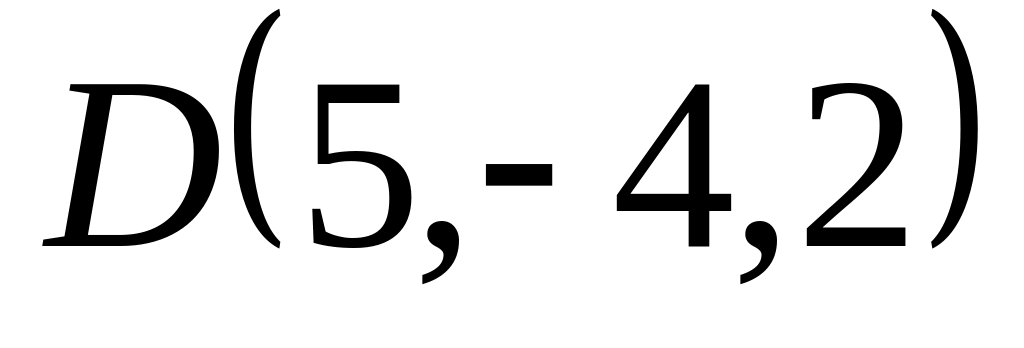 .
Проверить, что векторы
.
Проверить, что векторы
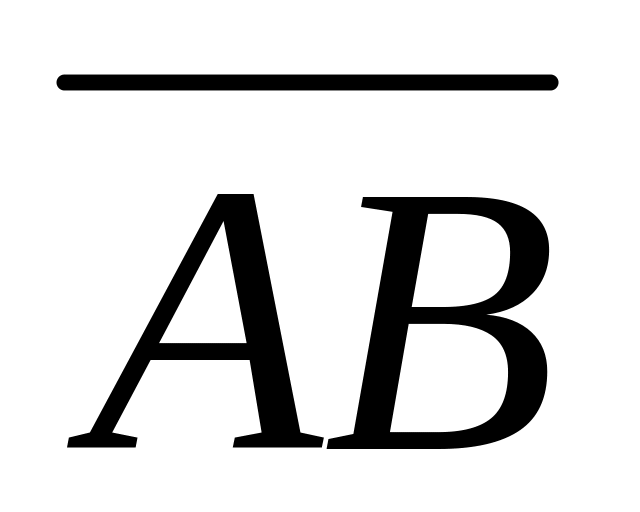 и
и
 коллинеарные; установить какой из них
длиннее другого и во сколько раз, как
они направлены – в одну или в
противоположные стороны.
коллинеарные; установить какой из них
длиннее другого и во сколько раз, как
они направлены – в одну или в
противоположные стороны.Даны три вектора , и , удовлетворяющие условию
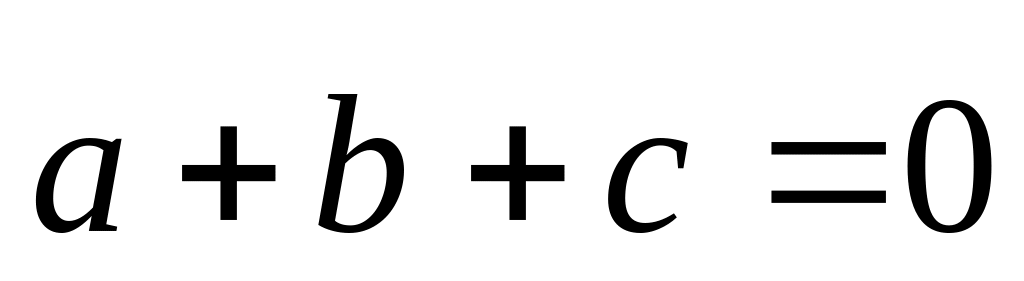 .
Зная, что
,
.
Зная, что
,
 и
и
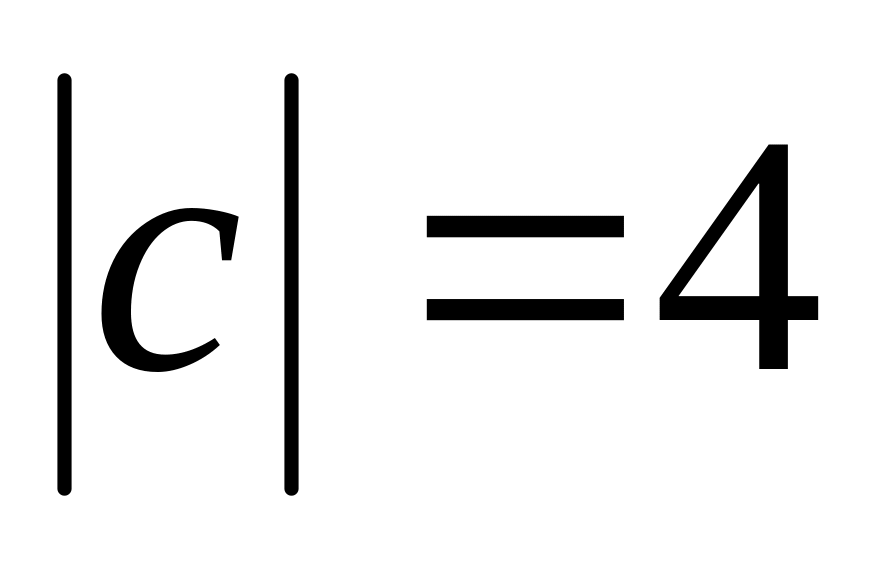 вычислить
вычислить
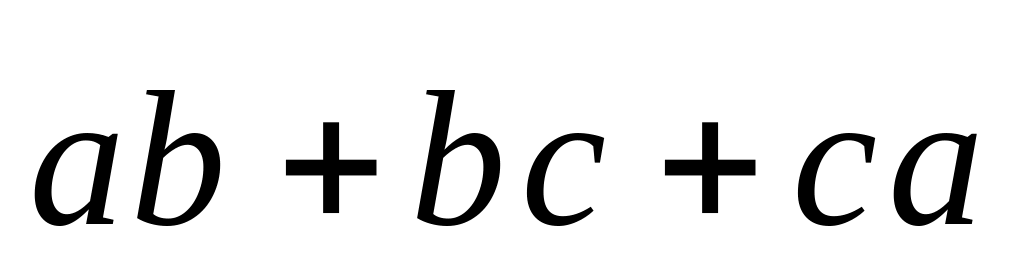 .
.Даны вершины треугольника
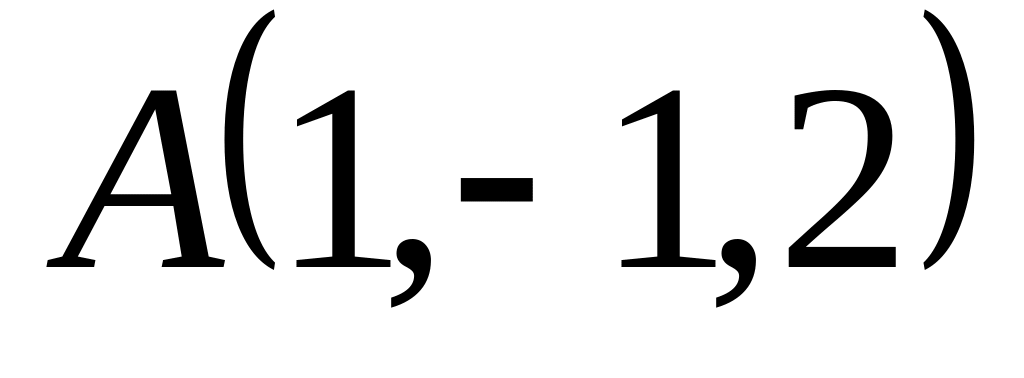 ,
,
 и
и
 .
Вычислить длину его высоты, опущенной
из вершины
.
Вычислить длину его высоты, опущенной
из вершины
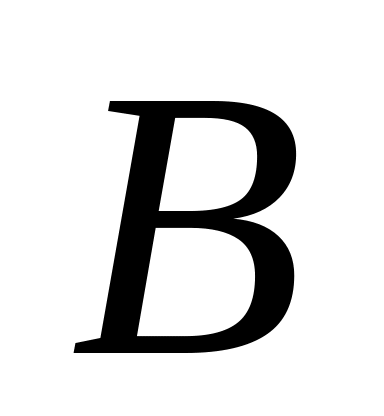 на сторону
на сторону
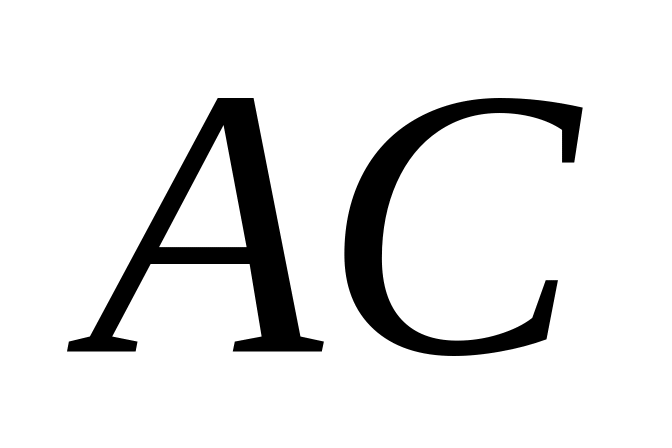 .
.Вычислить эксцентриситет эллипса, если расстояние от фокуса до дальней вершины большой оси в 1,5 раза больше расстояния до вершины малой оси.
В данной системе координат гипербола имеет каноническое уравнение. Составить это уравнение, если длина мнимой полуоси равна 1, а вершина гиперболы делит отрезок между фокусами в отношении 4:1.
Составить уравнение параболы, если ось параболы параллельна оси Oy, фокус лежит на оси Ox, парабола проходит через начало координат и высекает на оси Ox отрезок длины 6.
Составить уравнение касательной к кривой в точке .
Контрольная работа №4
Вариант 1
Найти ранг и базис системы векторов и выразить через этот базис системы векторов остальные векторы системы:
![]()
В зависимости от значения
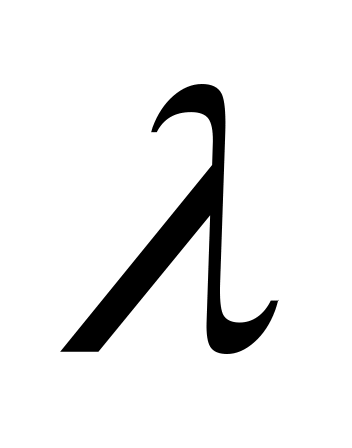 исследовать систему и найти общее
решение
исследовать систему и найти общее
решение

Найти собственные значения и собственные векторы матрицы, рассматриваемой как оператор умножения слева в пространстве столбцов над полем
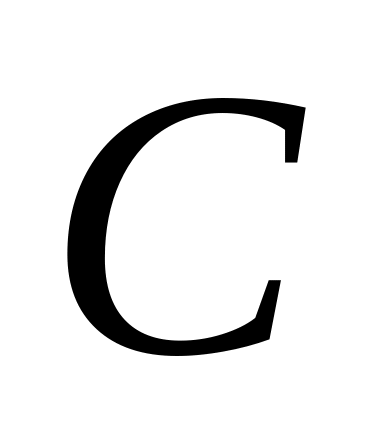 :
:
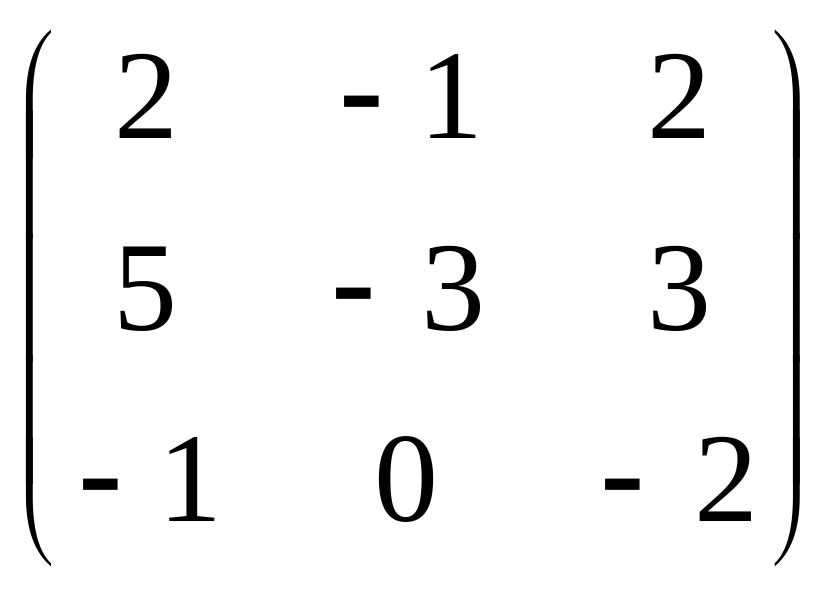
Вариант 2
Найти ранг и базис системы векторов и выразить через этот базис системы векторов остальные векторы системы:
![]()
В зависимости от значения исследовать систему и найти общее решение
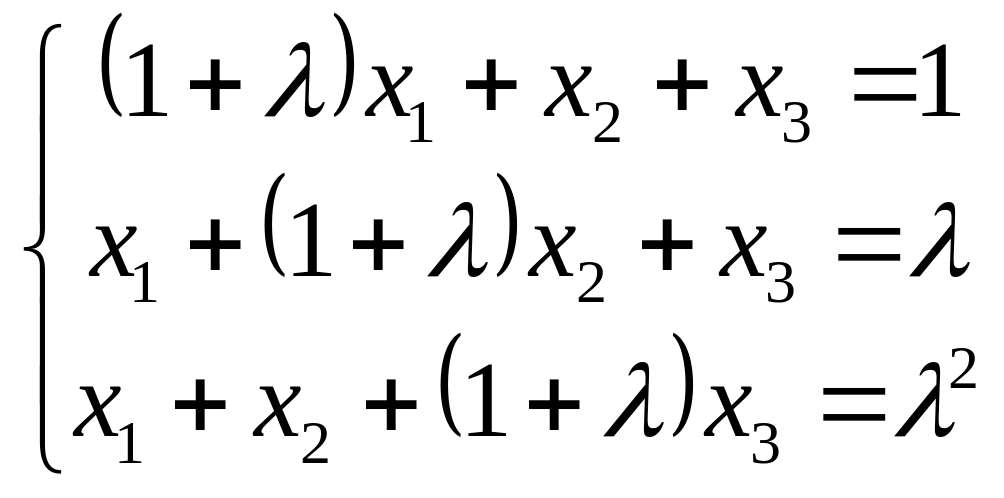
Найти собственные значения и собственные векторы матрицы, рассматриваемой как оператор умножения слева в пространстве столбцов над полем :
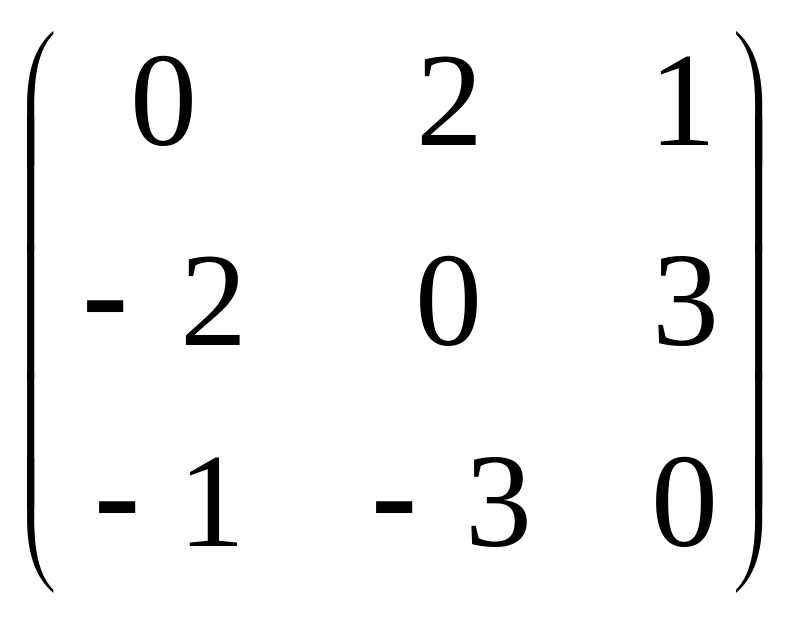
Вариант 3
Найти ранг и базис системы векторов и выразить через этот базис системы векторов остальные векторы системы:
![]()
В зависимости от значения исследовать систему при которых вектор
 линейно выражается через остальные
векторы
линейно выражается через остальные
векторы
![]()
Найти собственные значения и собственные векторы матрицы, рассматриваемой как оператор умножения слева в пространстве столбцов над полем :
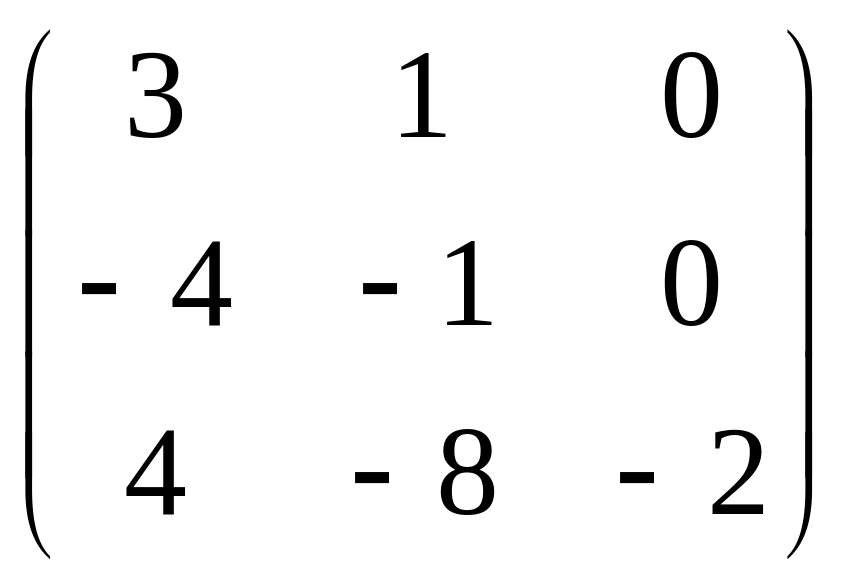
Вариант 4
Найти ранг и базис системы векторов и выразить через этот базис системы векторов остальные векторы системы:
![]()
В зависимости от значения исследовать систему при которых вектор линейно выражается через остальные векторы
![]()
Найти собственные значения и собственные векторы матрицы, рассматриваемой как оператор умножения слева в пространстве столбцов над полем :