
- •1. Место дисциплины в структуре ооп впо
- •2. Цели освоения дисциплины
- •3. Компетенции обучающегося, формируемые в результате освоения дисциплины (модуля)
- •Рабочая программа
- •Рабочая программа
- •Рабочая программа
- •Рабочая программа
- •5. Образовательные технологии
- •6. Учебно-методическое и информационное обеспечение дисциплины
- •7. Материально-техническое обеспечение дисциплины (модуля)
- •8. Методические рекомендации (материалы) для преподавателя
- •9. Методические указания для студентов
- •Темы лекционных занятий
- •Темы практических занятий Темы практических занятий
- •10. Учебно-методическое обеспечение самостоятельной работы студентов
- •11. Контрольно-оценочные материалы
- •Типовые задания для контрольных и самостоятельных работ.
- •Примерные контрольные работы Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа № 3
- •Примерные тестовые задания
- •Экзаменационные вопросы
- •Рейтинг-планы дисциплины по семестрам технологическая карта
- •Система оценивания
11. Контрольно-оценочные материалы
Контроль качества подготовки осуществляется путем проверки теоретических знаний и практических навыков путем:
1) промежуточных контрольных работ
2) проверки и приема текущих семестровых заданий
3) экзамена в конце 1 семестра.
В течение семестра студенты решают задачи, указанные преподавателем, к каждому семинару. В семестре проводится 3 контрольные работы (на семинарах).
По ходу изучения и усвоения студентами дисциплины «Линейная алгебра» рекомендуется проводить текущую и промежуточную аттестацию студентов.
Текущий контроль позволяет преподавателю отслеживать темпы усвоения материала, а промежуточный контроль должен свидетельствовать об итогах совместной работы преподавателя и студента по изучению данной дисциплины.
Текущий контроль успеваемости по итогам освоения дисциплины проводится в соответствие с положением о балльно-рейтинговой системе, принятой в НФ БашГУ. В течении каждого семестра (в середине и в конце) выставляются рейтинговые баллы студентов по дисциплине, учитывающие посещаемость студентов, активное участие на практических занятиях, выполнение контрольных и самостоятельных работ. Баллы по дисциплине «Линейная алгебра» выставляются в соответствие технологических карт (см. ниже).
Во время текущего контроля по дисциплине рекомендуется проводить и проверять контрольные работы по основным модулям дисциплины «Линейная алгебра»:
Контрольная работа №1 по темам: «Матрицы. Определители. Матричные уравнения. Системы линейных алгебраических уравнений»;
Контрольная работа №2 по темам: «Вектор. Базис. Скалярное, векторное, смешанное произведение векторов Линейные операторы. Действия над операторами»;
Контрольная работа №3 по темам: «Прямая на плоскости, в пространстве. Плоскость. Кривые второго порядка».
Каждая контрольная работа содержит также задачи из тем для самостоятельного изучения студентами. Каждая контрольная работа и каждая самостоятельная работа оцениваются согласно технологической карте дисциплины.
Важную роль при оценке самостоятельной работы играют консультации для студентов. Консультации проводятся 1 раз в неделю (соответственно графику консультаций) с целью оказания помощи в самостоятельной работе (написание конспекта, решения задач, выполнение курсовых работ, подготовка к экзамену, подготовка к конференции и т. д.).
Контроль полученных студентом в течение учебного года знаний и навыков осуществляется посредством промежуточной аттестации, которая проводится в соответствии с учебным планом и учебной программой в форме сдачи экзамена в конце 1-го семестра.
Типовые задания для контрольных и самостоятельных работ.
1. Решить уравнение А2 – 2(ВТ С)Т = DTX, где
А=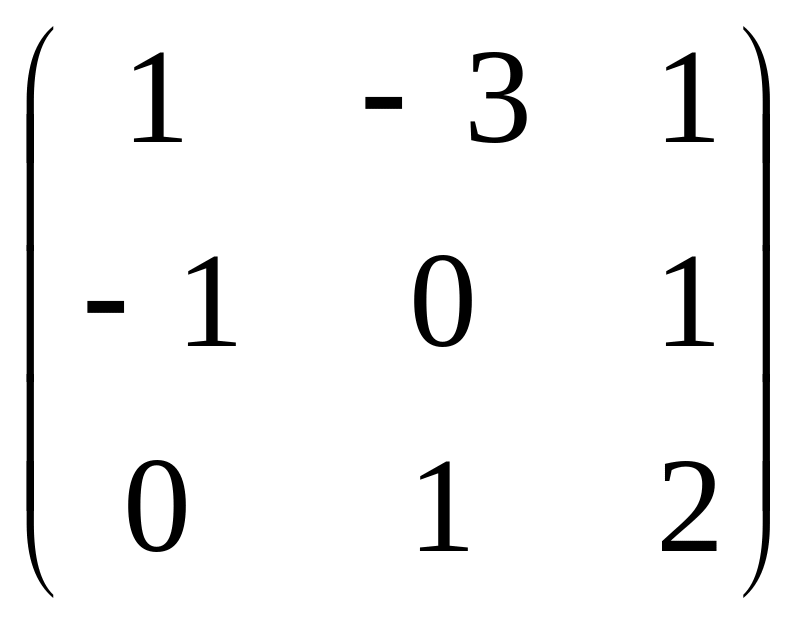 ,
,![]() ,
,![]() ,D=
,D=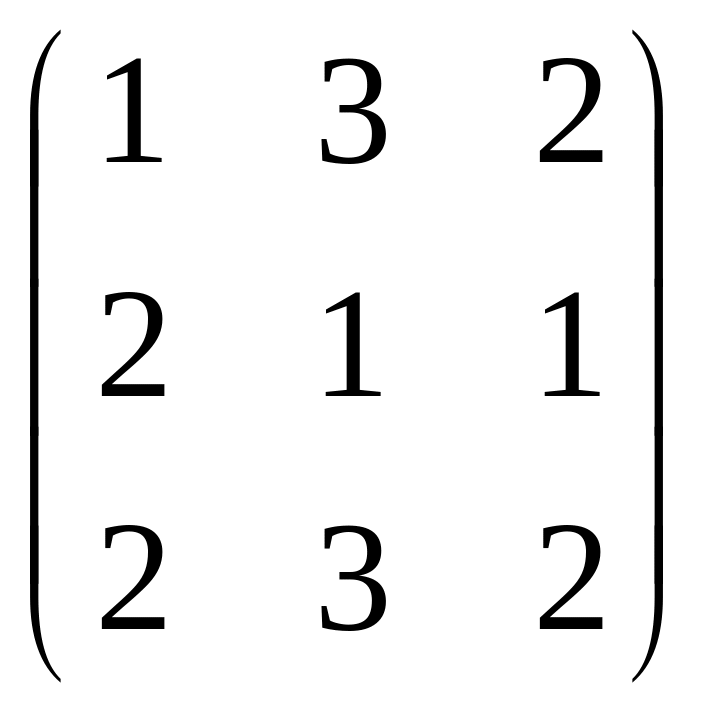
2. Вычислить определитель
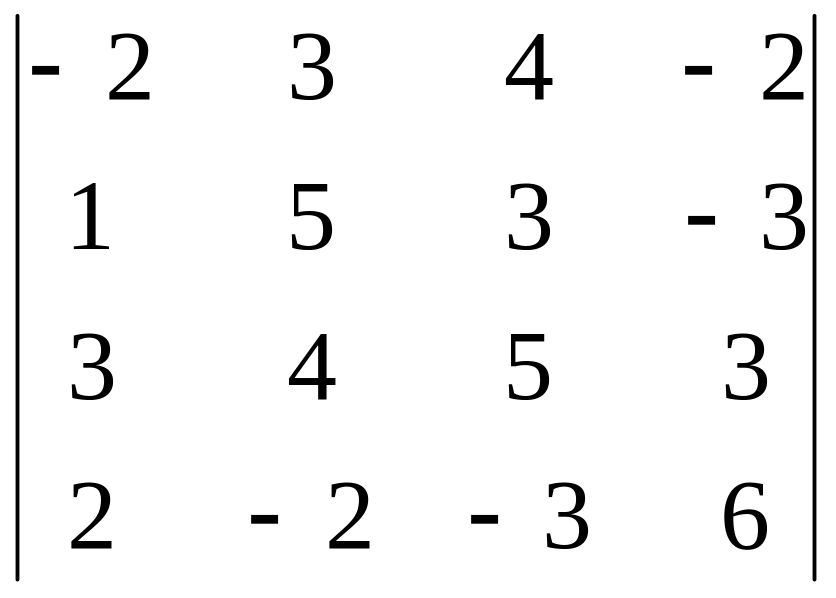
3. Найти общее решение системы уравнений, как сумму частного решения и ФСР
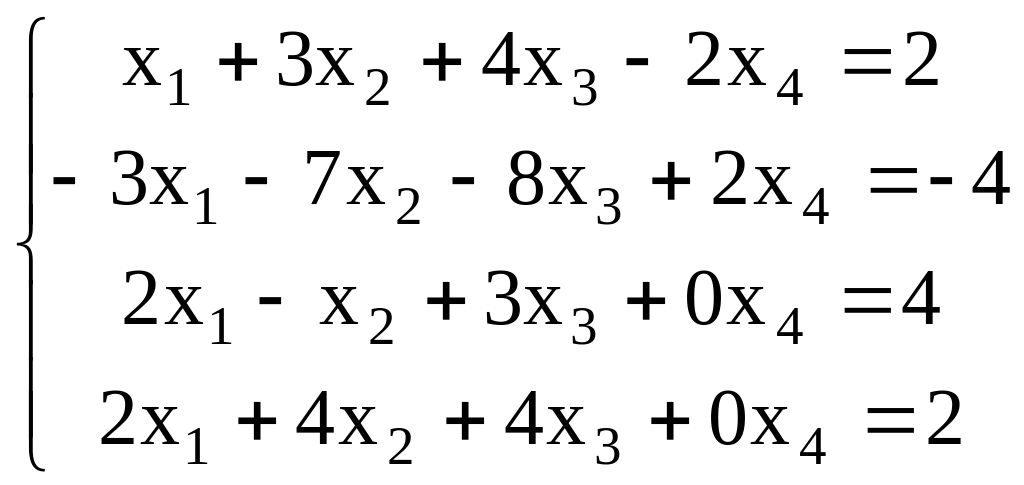
4. Решить уравнение А2 – (В СТ)Т = ХDT, где
А=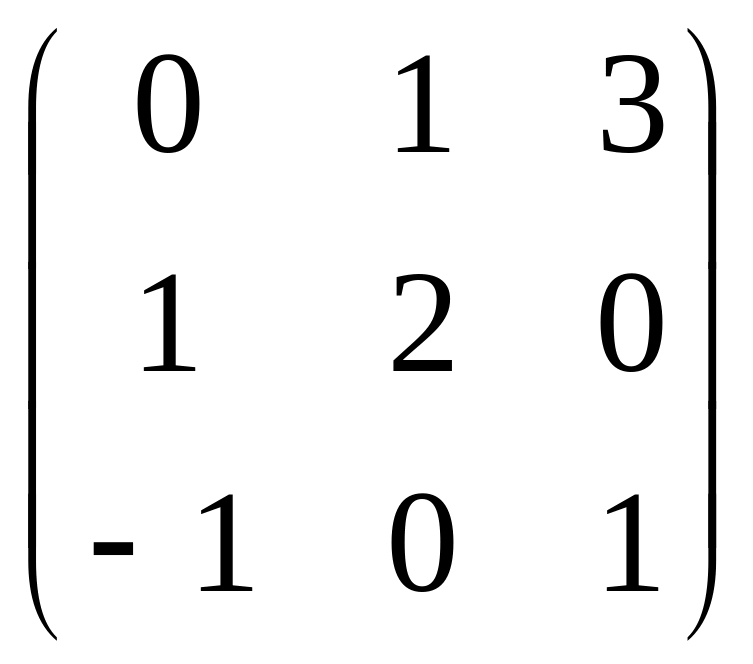 ,
,![]() ,
,![]() ,D=
,D=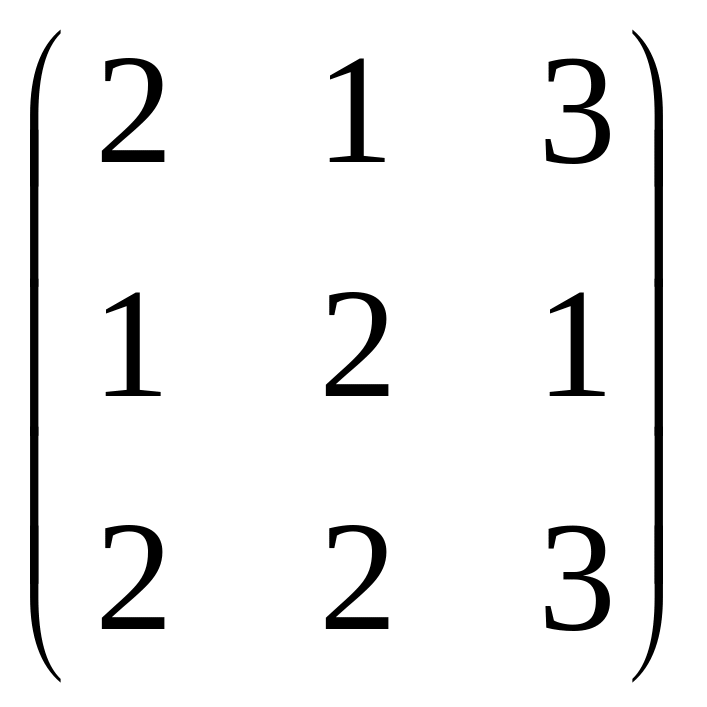
5. Вычислить определитель
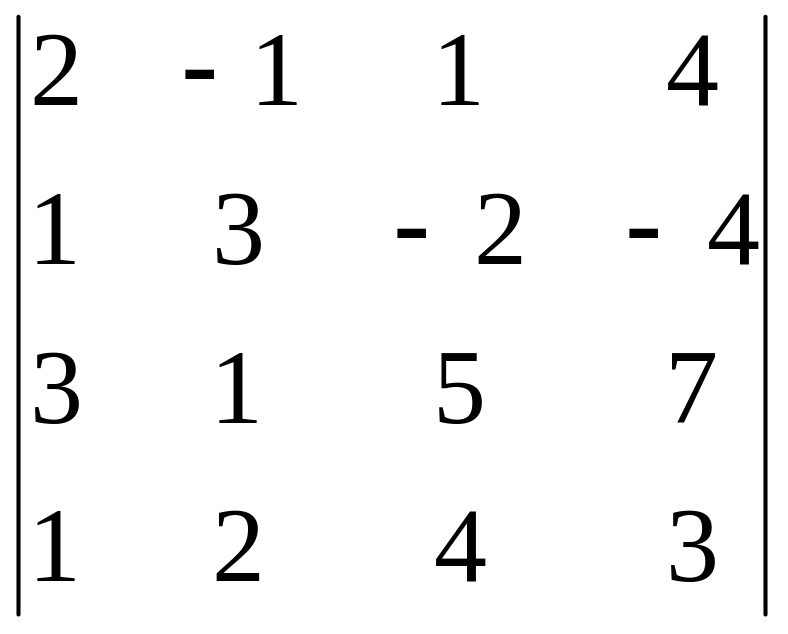
6. Найти общее решение системы уравнений, как сумму частного решения и ФСР

7. Решить уравнение А2 – 2СТВ = ХD, где
А= , , , D=
8. Вычислить определитель
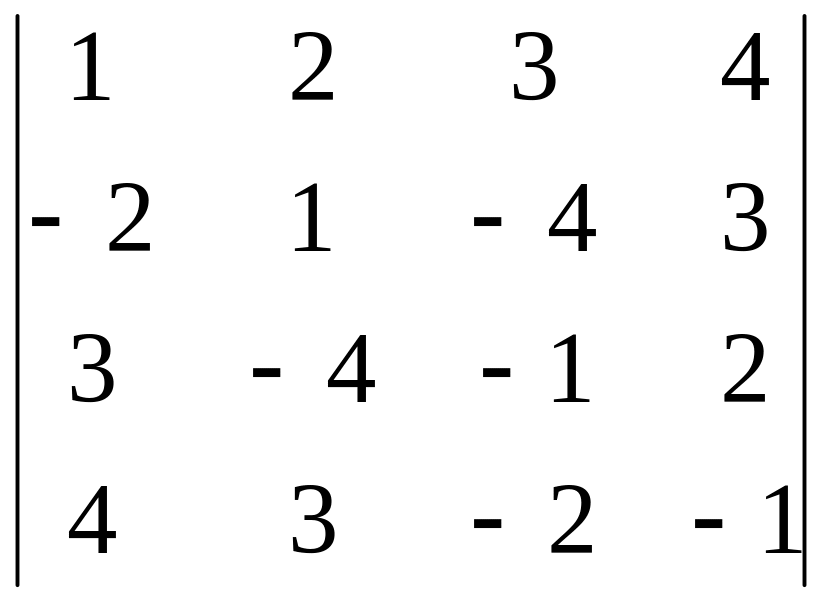
9. Найти общее решение системы уравнений, как сумму частного решения и ФСР
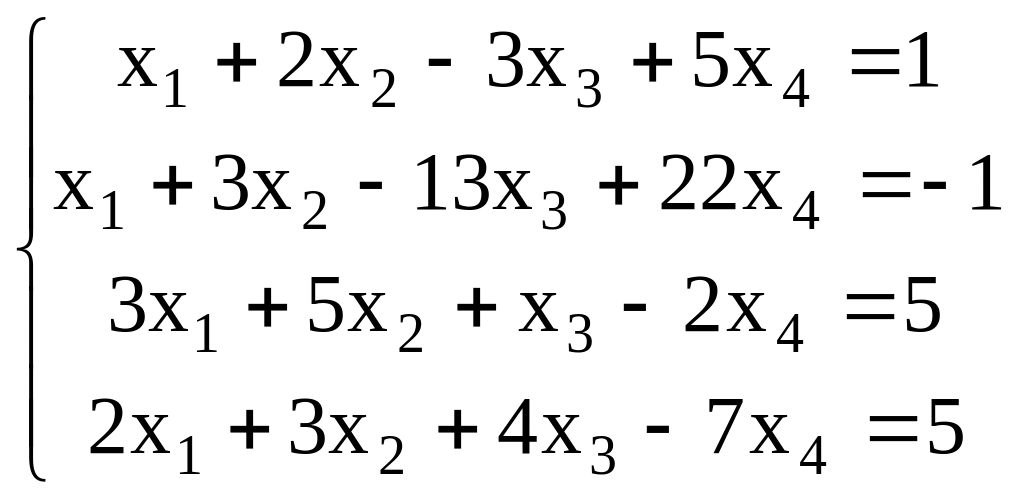
10. Решить уравнение А2 – С ВТ = DTХ, где
А= , , ,D=
11. Вычислить определитель

12. Найти общее решение системы уравнений, как сумму частного решения и ФСР
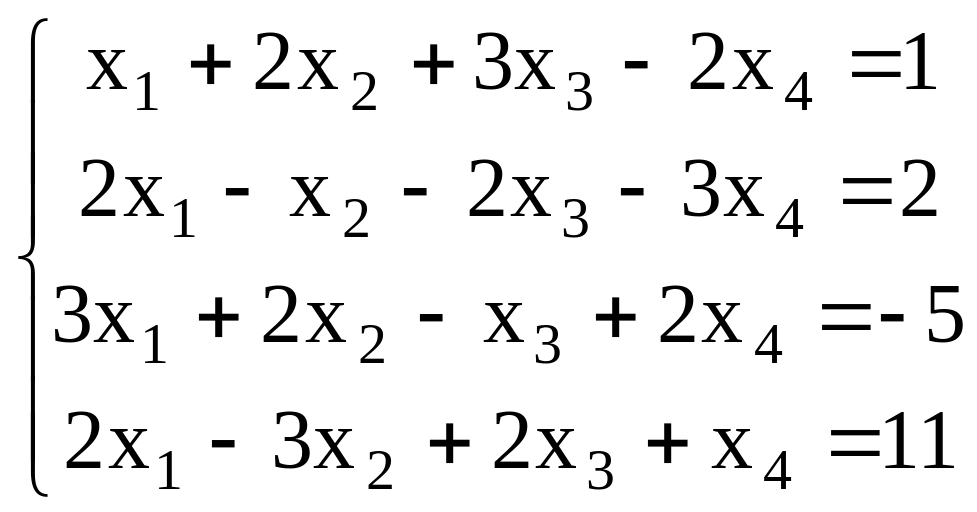
13. В некотором
ортонормированном базисе евклидова
пространства
![]() система элементов
система элементов
![]() представлена столбцами координат
представлена столбцами координат
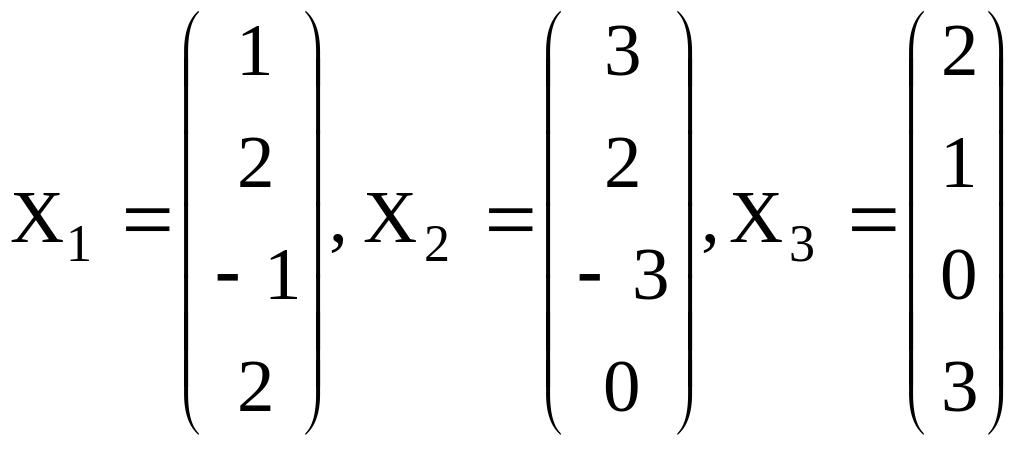 .
.
Требуется:
найти размерность и базис линейной оболочки
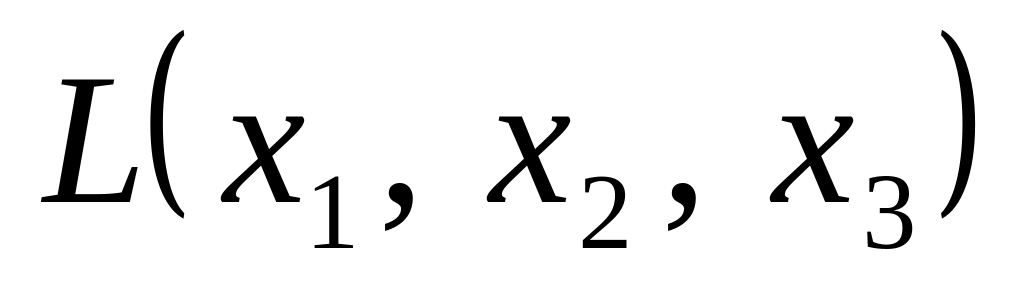 ;
;
указать в линейной оболочке ортонормированный базис и достроить его до ортонормированного базиса евклидова пространства .
14. В некотором ортонормированном базисе евклидова пространства система элементов представлена столбцами координат
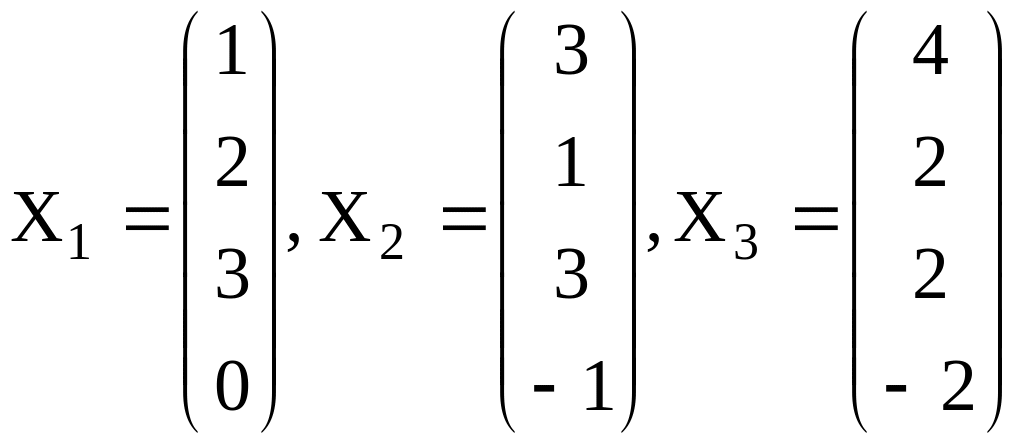 .
.
Требуется:
найти размерность и базис линейной оболочки ;
указать в линейной оболочке ортонормированный базис и достроить его до ортонормированного базиса евклидова пространства .
15. В некотором ортонормированном базисе евклидова пространства система элементов представлена столбцами координат
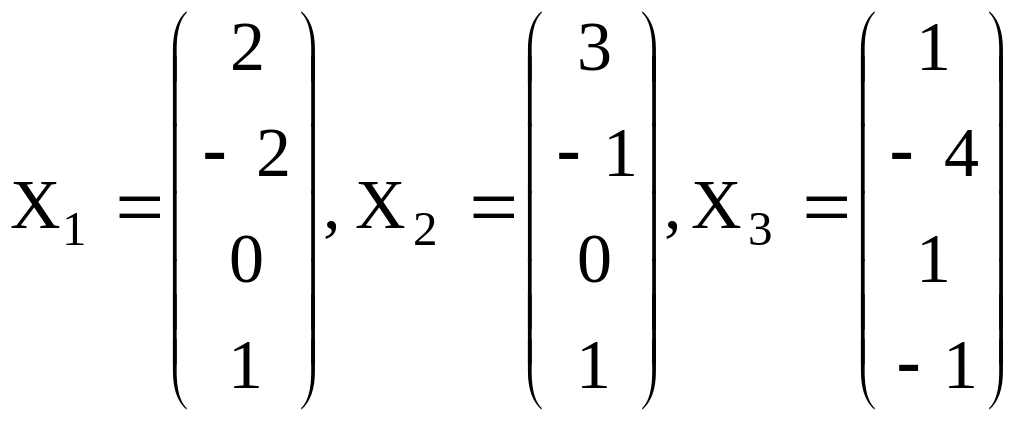 .
.
Требуется:
найти размерность и базис линейной оболочки ;
указать в линейной оболочке ортонормированный базис и достроить его до ортонормированного базиса евклидова пространства .
16. В некотором ортонормированном базисе евклидова пространства система элементов представлена столбцами координат
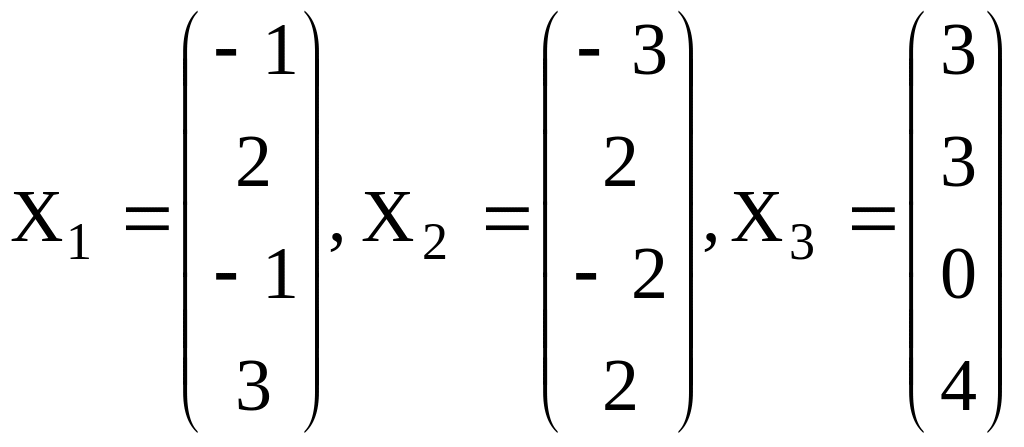 .
.
Требуется:
найти размерность и базис линейной оболочки ;
указать в линейной оболочке ортонормированный базис и достроить его до ортонормированного базиса евклидова пространства .
17. Дан треугольник с вершинами А(-2;0), В(2;6), С(4;2). Составить уравнения медианы ВМ, высоты ВД, найти их длины.
Даны вершины тетраэдра: А(2;3;1), В(4;1;-2), С(6;3;7), Д(-5;-4;8). Найти длину высоты тетраэдра, проведенной из вершины Д.
Составить уравнение плоскости, проходящей через две точки М(1;-1;-2) и Р(3;1;1) перпендикулярно к плоскости х-2у+3z-5=0.
Записать каноническое уравнение прямой 2х+3у+2z-4=0, х+4у+3z-6=0.
Найти расстояние между сторонами квадрата 2х-у+4=0 и 2х-у-1=0.
Найти координаты и длину вектора d, если d=3b+c-2a, где a(-3, 4, 1), b(4;1;-2), c(-3;2;-6).
Найти косинусы углов треугольника АВС, если А(1;2;6), В(0;3;8), С(-5;-1;4).
Дан график функции y=f(x). Построить графики функций 3f(x), f(x-1), f(½ x), - f(|x|), - f(x) +4.
Дан треугольник с вершинами А(-2;0), В(2;4), С(4;0). Составить уравнения медианы АМ, высоты АН, найти их длины.
Даны вершины тетраэдра: А(2;-1;1), В(5;5;4), С(3;2;-1), Д(4;1;3). Найти длину высоты тетраэдра, проведенной из вершины А.
Составить уравнение плоскости, проходящей через точки А(2;-1;4) и В(3, 5,-3), параллельной вектору а(-1, 3, 4).
Записать каноническое уравнение прямой 3х-2у+z-2=0, 4х+у-3z-2=0.
Найти расстояние между прямыми 3х-2у-5=0 и 3х-2у+5=0.
Найти координаты и длину вектора m, если m=2b-c+3a, где a(-3, 4, 1), b(4;1;-2), c(-3;2;-6).
Найти косинусы углов треугольника АВС, если А(2;1;1), В(6;-2;2), С(4;3;2).
Дан график функции y=f(x). Построить графики функций 2f(x), f(x+2), f(1/3 x), f(|x|), - |f(x)|.
Векторы
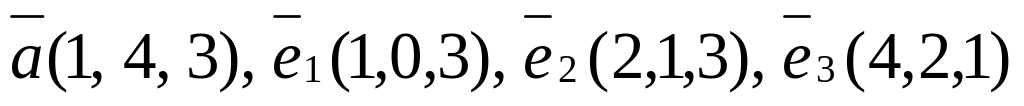 заданы в некотором базисе координатами.
Доказать, что векторы можно взять в
качестве нового базиса и разложить
вектор
заданы в некотором базисе координатами.
Доказать, что векторы можно взять в
качестве нового базиса и разложить
вектор
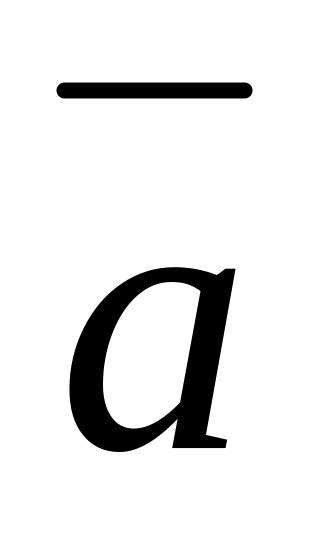 по
этому базису.
по
этому базису.9) Найти характеристические числа и собственные векторы линейного преобразования А, матрица линейного преобразования
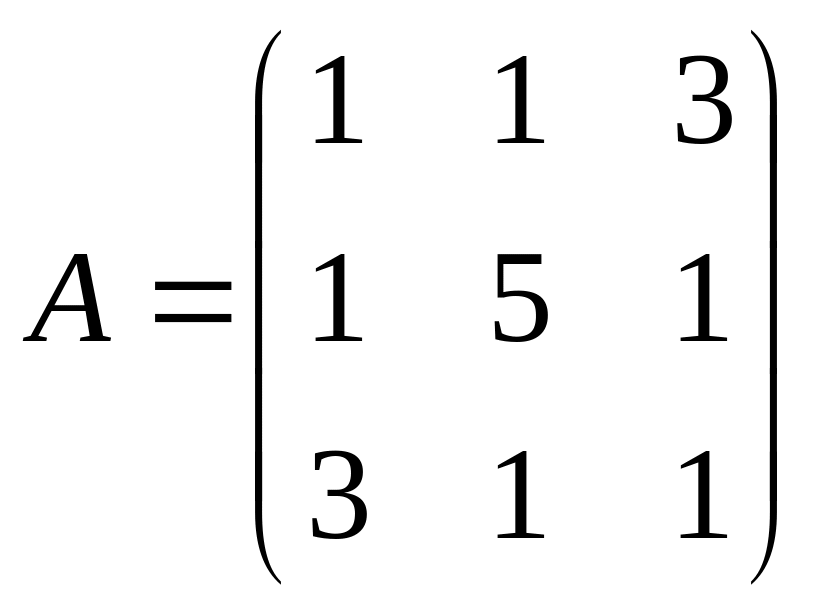 .
.Векторы
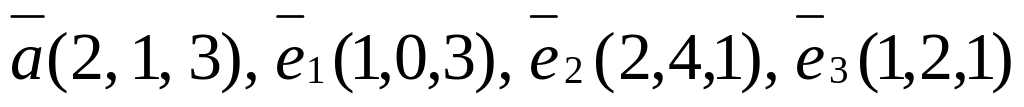 заданы в некотором базисе координатами.
Доказать, что векторы можно взять в
качестве нового базиса и разложить
вектор
по
этому базису.
заданы в некотором базисе координатами.
Доказать, что векторы можно взять в
качестве нового базиса и разложить
вектор
по
этому базису.9) Найти характеристические числа и собственные векторы линейного преобразования А, матрица линейного преобразования
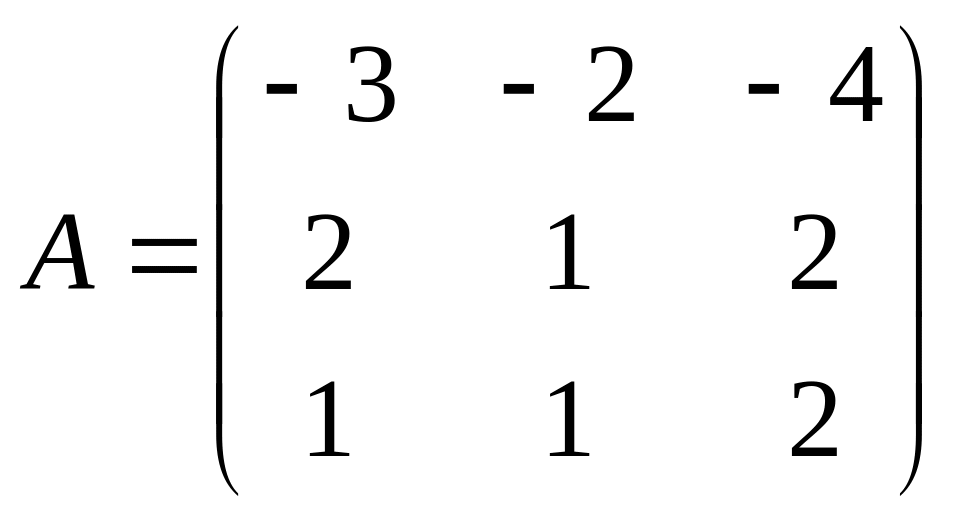
Векторы
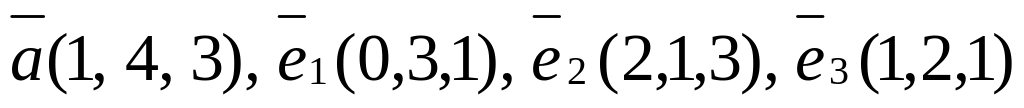 заданы в некотором базисе координатами.
Доказать, что векторы можно взять в
качестве нового базиса и разложить
вектор
по
этому базису.
заданы в некотором базисе координатами.
Доказать, что векторы можно взять в
качестве нового базиса и разложить
вектор
по
этому базису.9) Найти характеристические числа и собственные векторы линейного преобразования А, матрица линейного преобразования .
