1. Фазы складываемых колебаний одинаковы.

.

В этом случае

И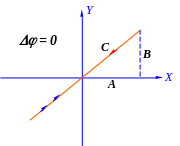 сключая из приведенных уравнений , получим уравнение результирующего движения точки. Это уравнение прямой, лежащей в первой и третьей четвертях.

Из полученного соотношения следует, что результирующее движение точки является прямолинейным движением. Легко видеть, что это движение будет гармоническим колебанием с частотой исходных колебаний.

Этот результат непосредственно следует из исходных уравнений (1) и (2) и из (3)

,

Аналогичные результаты следуют и из (3)

2. Рассмотрим случай, когда разность фаз складываемых колебаний равна и :

В этом случае

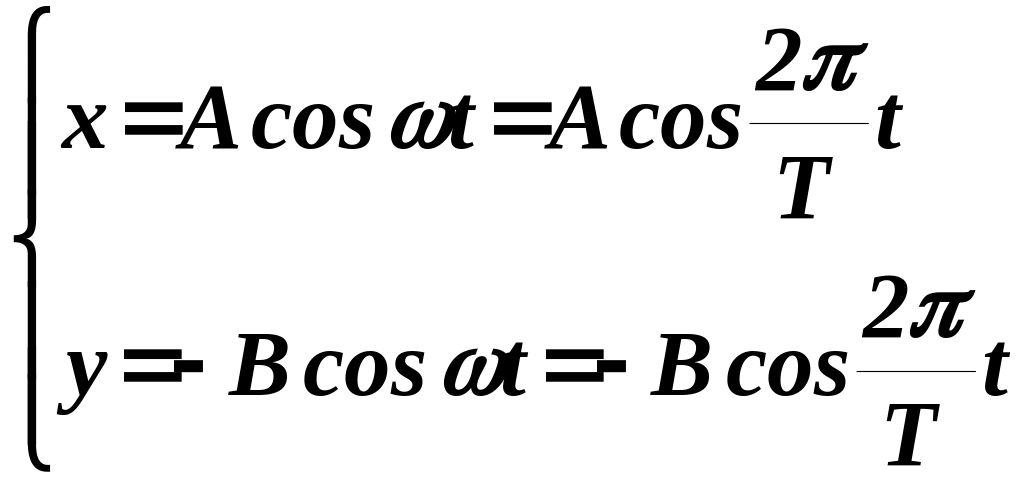
Уравнение траектории будет иметь вид

Это уравнение прямой, лежащей в второй и четвертой четвертях. Результирующее движение точки также будет гармоническим колебанием

, Амплитуда которого с .

Очевидно, что этот результат можно получить также из (3).

3. Разность фаз равна .в этом случае

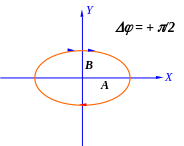
Как следует из (3), уравнением траектории точки будет эллипс, главные оси которого совпадают с осями координат.

,

Этот результат непосредственно следует и из соотношений, описывающих складываемые колебания.

.

Б олее детальный анализ указывает на то, что движение точки будет происходить по эллипсу в направлении против стрелки часов.

К огда амплитуды складываемых колебаний одинаковы, т. е. , то результирующее движение точки будет представлять собой равномерное движение по окружности радиусом в направлении против стрелки часов. Это значит, что равномерное движение по окружности представляет собой сумму двух гармонических колебаний во взаимно-перпендикулярных направлениях с равными частотами и одинаковыми амплитудами.

4. . В этом случае

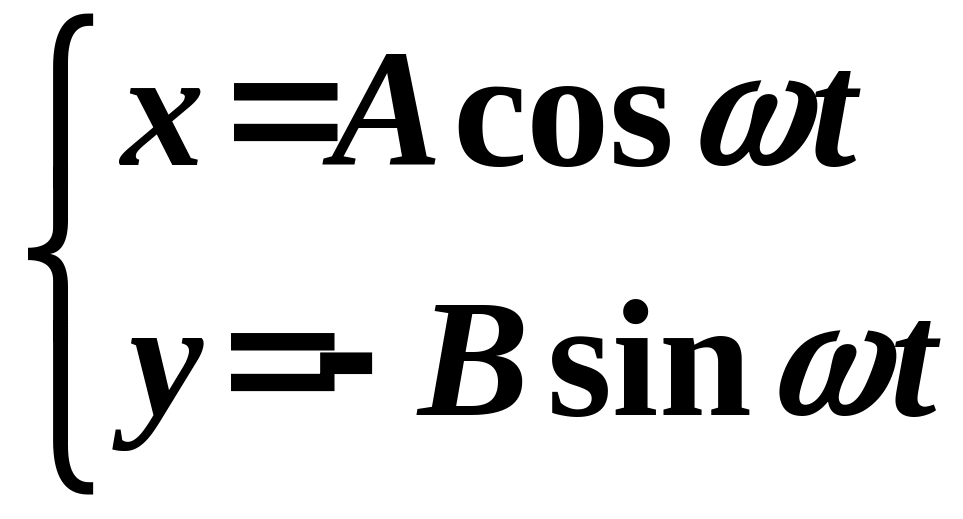
Как легко видеть, в этом случае траекторией результирующего движения является эллипс. Точка движется в направлении часовой стрелки.

Если складываемые колебания имеют не равные, но близкие частоты, то разность фаз колебаний будет непрерывно меняться, последовательно принимая все значения фазы от до :

В результате траектория результирующего движения с течением времени будет изменяться, принимая формы, представленные на рисунке.

, , .

Если складываемые колебания имеют произвольные, неравные друг другу частоты, результирующее движение точки будет происходить по некоторой сложной кривой, которую называют фигурой Лиссажу.

, .

Когда частоты складываемых колебаний относятся как целые числа, фигура Лиссажу будет представлять собой замкнутую кривую. По виду кривой легко найти отношение складываемых частот. Для этого нужно воспользоваться следующим мнемоническим правилом. В соответствии с этим правилом произведение числа пересечений фигуры Лиссажу прямой, параллельной оси , на частоту колебаний вдоль оси равно произведению числа пересечений фигуры Лиссажу прямой, параллельной оси , на частоту вдоль оси . Т.е. справедливо соотношение:

;

Здесь: - число пересечений фигуры Лиссажу с ;

- число пересечений фигуры Лиссажу с ;

- частота колебаний вдоль ;

- частота колебаний вдоль .

Очевидно, что частным случаем фигуры Лиссажу является эллипс (окружность), для которого

и .

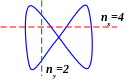В качестве другого частного случая рассмотрим фигуры в виде горизонтальной или вертикальной «восьмёрки», которые получаются при сложении колебаний с частотами, относящимися как 1 : 2 или 2 : 1.

И з приведенного рисунка следует, что частота колебаний вдоль оси в два раза ниже частоты колебаний вдоль оси . Другой пример.