Запись колебаний

Гармоническое колебание представляет собой один из видов одномерного движения. Когда гармоническое колебание представляют уравнением:

траекторией является отрезок прямой длинной в , направленный вдоль оси .

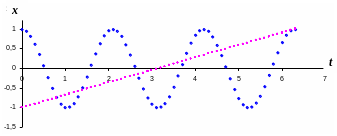
Уравнение движения представляет некоторую зависимость . Такая зависимость строится в координатах и . Очевидно, что для гармонического колебания она будет представлять собой косинусоиду. Представление гармонического колебания в координатах и называют записью гармонических колебаний. Можно выделить два основных способа записи колебании.

1. Механический способ записи колебаний.

2. Электронная запись колебаний с помощью осциллографа.

Рассмотрим электронный способ записи колебаний.

В случае электронной записи колебаний используют осциллограф, основной частью которого является электронно-лучевая трубка. В ней имеются две пары взаимно-перпендикулярных пластин, управляющих движением узкого пучка электронов (электронного луча). Пластины, отклоняющие электроны в вертикальном направлении называются – пластинами. Пластины, отклоняющие электроны в горизонтальном направлении – пластинами.

Если на – пластины подать напряжение, изменяющееся по гармоническому закону

то электронный луч будет совершать гармонические колебания в направлении оси . На экране осциллографа будет наблюдаться светящийся след в виде отрезка прямой, направленной вдоль вертикали. Длина этого отрезка пропорциональна удвоенному амплитудному напряжению. Чтобы получить на экране изображение процесса колебаний, развёрнутого во времени, необходимо подать напряжение и на пластины . Это напряжение называют напряжением развертки. Оно обеспечивает равномерное движение луча в горизонтальном направлении. В результате на экране осциллографа электронный луч будет вычерчивать синусоиду.

Сложение двух гармонических колебаний одного направления с равными частотами

Если точка одновременно участвует в нескольких гармонических колебаниях, обусловленных различными квазиупругими силами, то в соответствии с принципом независимости действия сил результирующее смещение точки будет равно векторной сумме смещений, полученных в каждом отдельном колебании.

Здесь - смещения, полученные в каждом отдельном колебании.

1. Пусть некоторая точка одновременно участвует в двух гармонических колебаниях с равными частотами, происходящими в направлении оси ох. Пусть эти колебания описываются уравнениями:

(1)

В соответствии с принципом суперпозиции смещений результирующее смещение точки будет равно:

Для определения характера зависимости результирующего смещения от времени необходимо выполнить сложение двух тригонометрических функций. Такое сложение удобно провести с помощью векторной диаграммы.

Д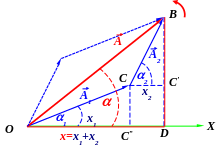 ля этого на векторной диаграмме представим складываемые колебания для момента .

Очевидно, что вектор , равный векторной сумме векторов и , представляет амплитуду результирующего колебания, а угол , который он составляет с осью ОХ в момент , равен начальной фазе этого колебания. Так как складываемые колебания имеют одинаковые частоты, векторы и будут вращаться с одной и той же скоростью, и угол между ними изменяться не будет. С той же скоростью будет вращаться и вектор , величина которого будет оставаться неизменной. Таким образом, треугольник OCB будет вращаться как твердое тело с угловой скоростью . Это значит, что результирующее колебание, характеризуемое смещением , будет представлять собой гармониче­ское колебание той же частоты

Для установления связи амплитуды и фазы с амплитудами и и начальными фазами и рассмотрим штрихованный треугольник ОСВ. По теореме косинусов из треугольника ОСВ следует

,

так как угол С равен

, то

(2)

Для нахождения начальной фазы рассмотрим треугольник ОВD. Из следует, что

(3)

Р ассмотрим ряд частных случаев: