Момент импульса. Закон сохранения момента импульса

Векторное произведение радиус-вектора точки на ее импульс

называют моментом импульса точки. Момент импульса тела или системы точек равен векторной сумме моментов импульсов всех его точек.

Подсчитаем момент импульса материальной точки массы m, равномерно движущейся по окружности радиуса R

,

, ,

, ,

(1)

Момент импульса плоского тонкого диска, вращающегося относительно оси, перпендикулярной плоскости диска, определится аналогичным соотношением

.

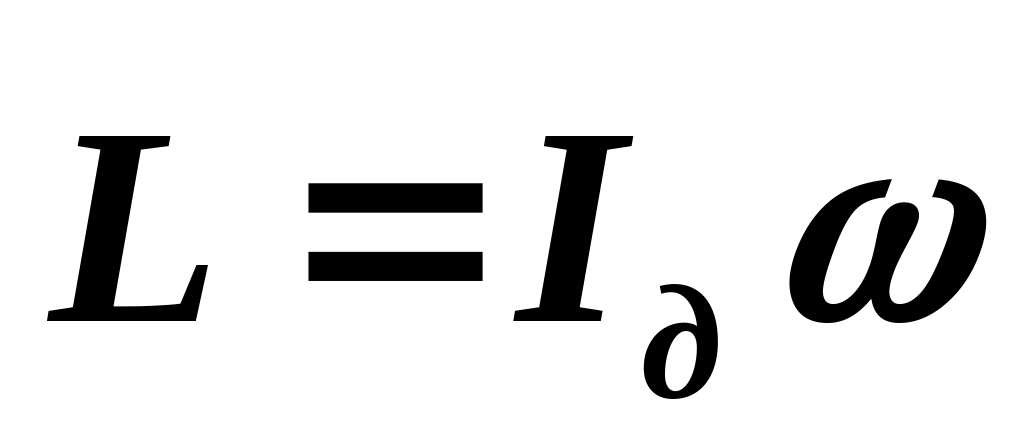Диск представляет собой совокупность материальных точек, для каждой из которых справедливо соотношение

; ; .

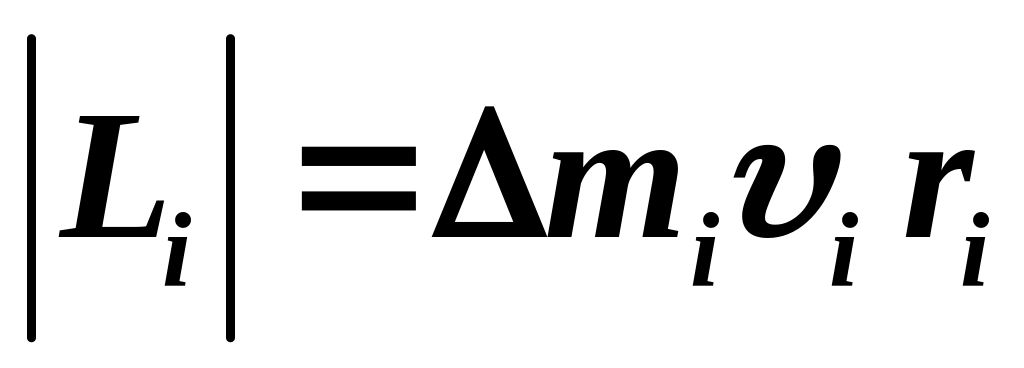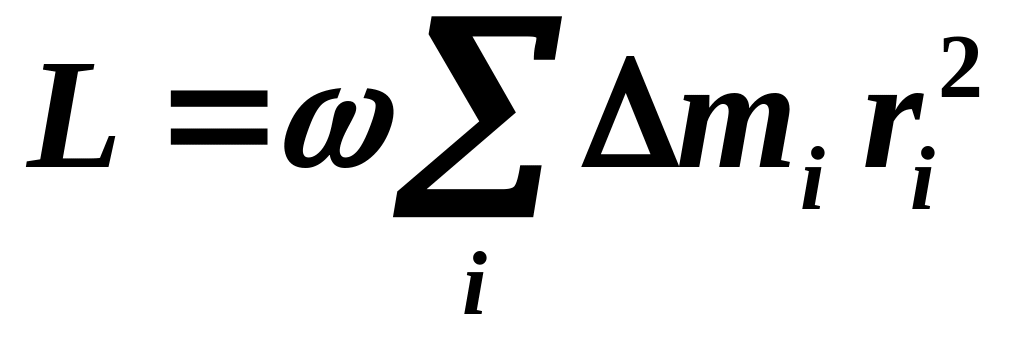В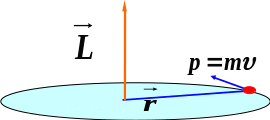 модели атома водорода Бора величина момента импульса электрона принимает дискретные значения

, .

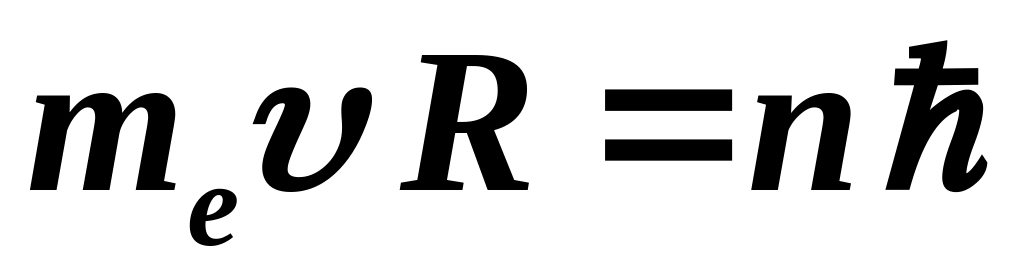где , целые числа.

В соответствии со 2-м законом Ньютона для вращающихся тел

.

Принимая во внимание, что угловое ускорение ,

можно получить

.

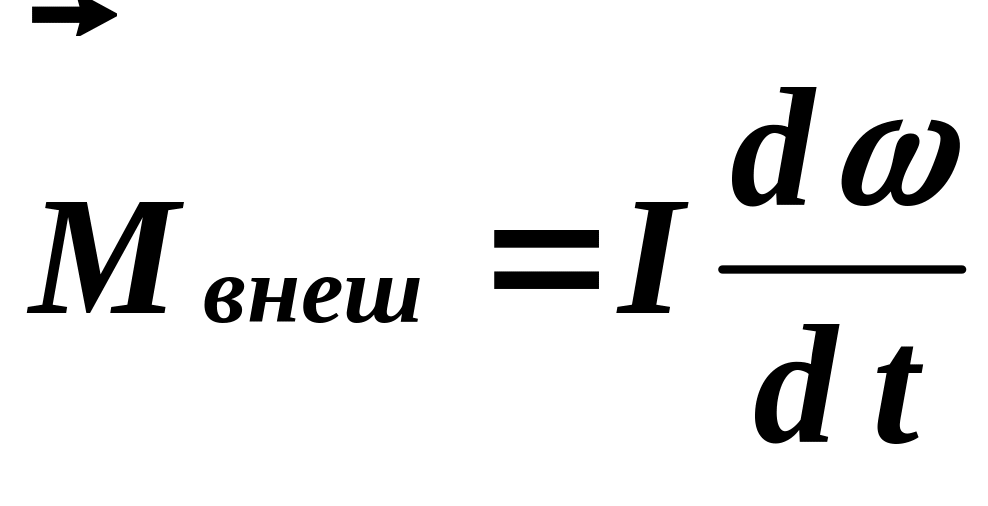Если момент инерции тела I является постоянной величиной, то его можно внести под знак дифференциала и в результате получить одно из фундаментальных соотношений механики – уравнение моментов.

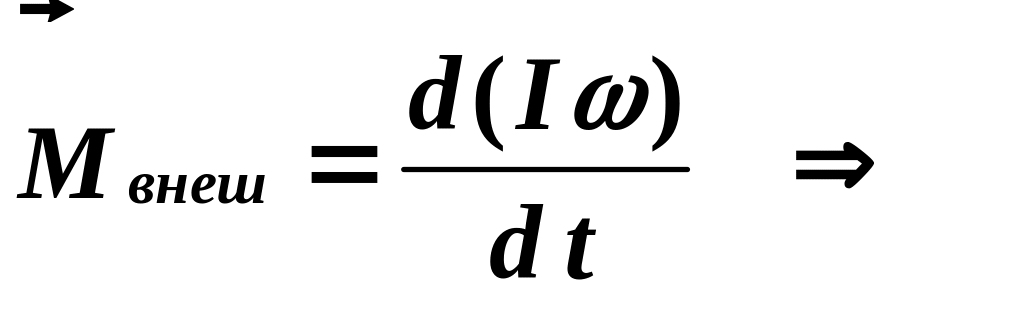
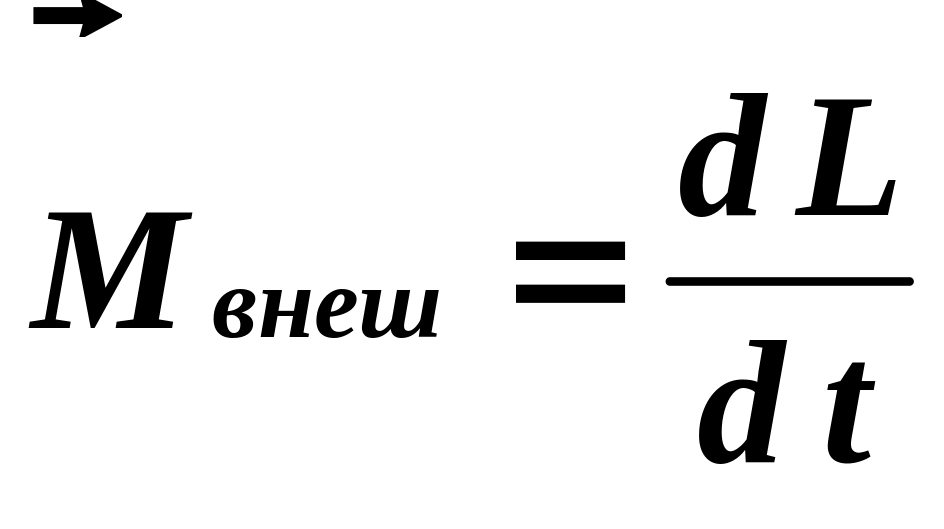
Приведенное уравнение моментов справедливо для любых тел и является фундаментальным соотношением физики. В соответствии с этим уравнением

скорость изменения момента импульса механической системы равна результирующему моменту внешних сил.

Покажем справедливость уравнения моментов длясистемы, состоящей из материальных точек.

Применим к каждой частице тела 2-й закон Ньютона в общей форме

.

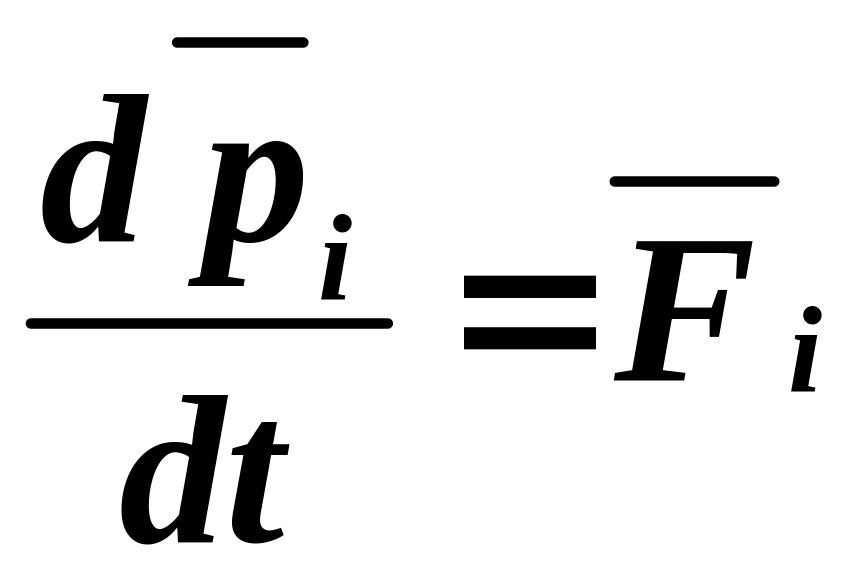Каждое соотношение умножим векторно слева на радиус-вектор соответствующей точки. В результате получим

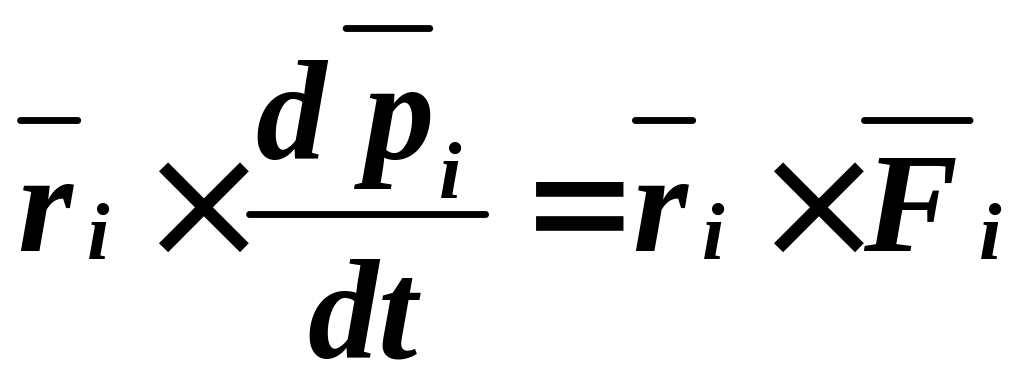. (2)

Обратим внимание на то, что радиус-вектор можно внести под знак дифференциала

.

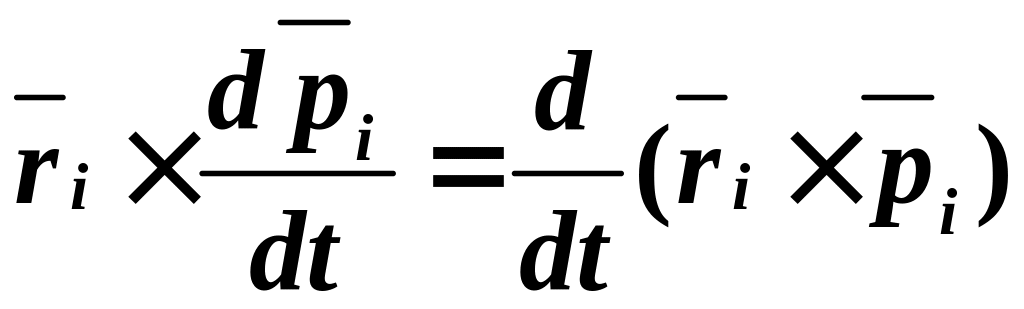В самом деле, дифференцируя векторное произведение,

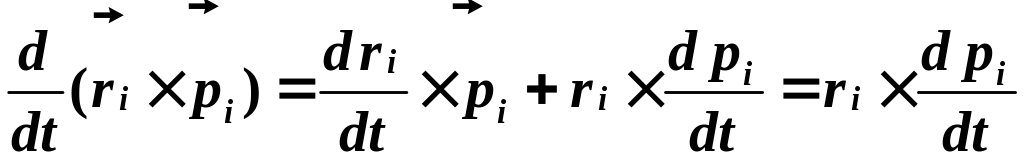
получим.

Производя суммирование левых и правых частей (2) по всем точкам тела, получим

Левая сумма представляет собой момент импульса всех точек тела, а правая сумма является моментом внешних сил, действующих на тело. Результирующий момент внутренних сил в силу 3-го закона Ньютона равен нулю. Таким образом, для любой механической системы справедливо соотношение, которое называют уравнением моментов или 2-м законом Ньютона для вращающихся тел. В соответствие с этим законом скорость изменения момента импульса системы равна результирующему моменту сил, действующих на нее

.

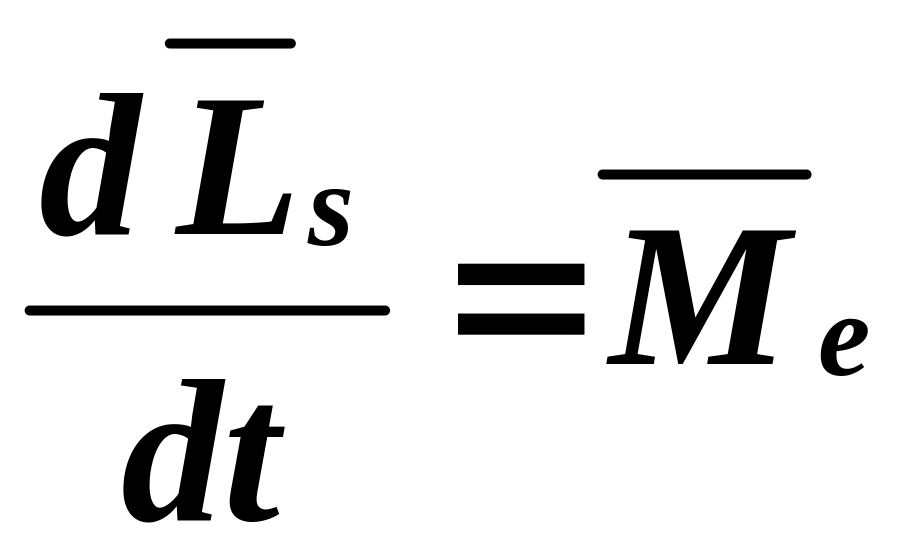Если момент внешних сил равен нулю, то момент импульса системы с течением времени не изменяется ни по направлению, ни по величине. Это утверждение является содержанием одного из фундаментальных законов ПРИРОДЫ – закона сохранения момента импульса.

Приведем примеры проявления Закона сохранения момента импульса.

1 . Момент импульса Земли - вращающейся вокруг своей оси, остается неизменным и по величине, и по направлению, т.К. Момент силы тяготения, действующий на Землю со стороны Солнца равен 0.

Одновременно с этим вследствие закона сохранения момента импульса орбита Земли является плоской кривой – эллипсом, т.к. сохраняется момент импульса Земли, связанный с ее движением вокруг Солнца.

2. Пусть, при условии , некоторое тело с моментом инерции I₁ вращается с угловой скоростью . Если в результате действия внутренних сил момент инерции тела изменится и станет равным I₂, то его угловая скорость также изменится и станет равной . Величину этой угловой скорости можно определить, используя закон сохранения момента импульса. При любых взаимодействиях между телами системы . Поэтому

Из приведенной формулы следует, что угловая скорость тела возрастет, если его момент инерции уменьшится, и станет меньше, когда возрастет момент инерции тела. Примеры, подтверждающие эти выводы, можно найти повсюду: при уменьшении момента инерции тела фигуриста или балерины их скорость вращения увеличивается, увеличивается скорость вращения гимнаста или акробата при группировке и т.п. Множество опытов, подтверждающих справедливость закона сохранения момента импульса, можно продемонстрировать на скамье Н.Е. Жуковского.

3. Пусть момент импульса изолированной системы из двух тел равен 0. Если в результате действия внутренних сил одно из тел с моментом инерции I₁, начнет вращаться с угловой скоростью , то другое тело системы с моментом инерции I₂ придет во вращательное движение в противоположном направлении. Угловая скорость вращения второго тела определится из закона сохранения момента импульса.

Как видим, второе тело будет вращаться в противоположную сторону. Об этом свидетельствует знак «минус» в полученном соотношении. Величина угловой скорости будет тем больше, чем меньше момент инерции второго тела в сравнении с первым. Например, если статор электродвигателя не закрепить на фундаменте, то при включении электродвигателя он начнет вращаться в противоположном ротору направлении.