Динамика твердого тела Второй закон Ньютона для вращающихся твердых тел

Когда размерами тела пренебречь нельзя, его рассматривают как совокупность материальных точек. Тело называют абсолютно твердым, если расстояния между точками тела не изменяются. Это вторая абстракция механики.

Поступательным называют движение, при котором точки тела имеют одинаковые перемещения, скорости и ускорения. Описание поступательного движения сводится к описанию движения его центра масс.

Вращательным называют движение, при котором точки тела имеют одинаковые угловые перемещения, скорости и ускорения. Вращение характеризуют углом поворота.

Произвольное движение твердого тела представляет собой векторную сумму поступательного и вращательного движений.

Ускорение центра масс тела определяется соотношением

При поступательном движении инертные свойства тела характеризует масса тела. Действие на тело определяется результирующей внешних сил.

При вращательном движении в качестве меры инертности тела и меры, действующих на него других тел, используют другие величины – момент инерции и момент силы. Угловое ускорение тела, определяется формулой

.

Здесь момент внешних сил, момент инерции тела. Угловое ускорение прямо пропорционально результирующему моменту сил и обратно моменту инерции тела. Приведенное соотношение будем называть 2-м законом Ньютона для вращающихся твердых тел.

М омент инерции тела?

Момент инерции точки массы m , находящейся на расстоянии r от оси вращения, равен произведению массы точки на квадрат ее расстояния до оси вращения

i = m r².

Момент инерции твердого тела равен сумме моментов инерции всех его точек.

Или более точно

Вычисление моментов инерции тел является не простой математической задачей.

В случае однородных тел симметричной формы моменты инерции вычисляются сравнительно легко.

1 . Определим момент инерции тонкого однородного обруча, масса которого m и радиус r , относительно оси, проходящей через центр масс перпендикулярно плоскости, в которой лежит обруч.

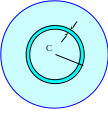
2. Определим момент инерции тонкого однородного диска, относительно оси, проходящей через центр масс диска, перпендикулярно плоскости диска. Пусть ρ - плотность, а - толщина диска.

Представим диск в виде совокупности тонких колец разного радиуса. Момент инерции каждого такого кольца, радиус которого r_i и ширина Δr_i ,

ж

Момент инерции диска будет равен сумме моментов инерции всех колец.

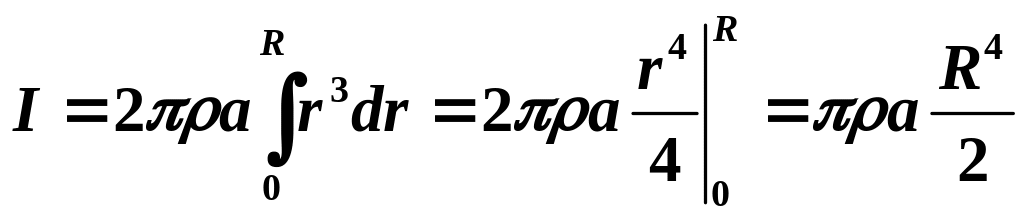
3 . Однородный прямой круговой цилиндр можно представить в виде стопки тонких однородных дисков. Поэтому момент инерции цилиндра относительно оси, проходящей через его центр масс параллельно образующей, равен:

Приведем формулы для подсчета моментов инерции некоторых других тел.

М омент инерции однородного шара относительно оси, проходящей, через его центр масс:

М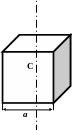 омент инерции однородного куба массой и ребром относительно оси, проходящей центр масс, перпендикулярно противоположным граням, равен

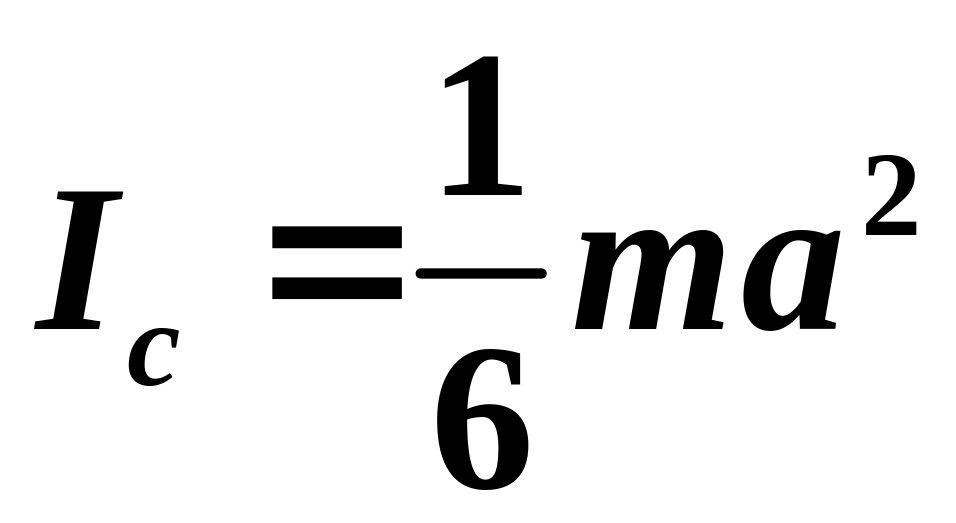
Момент инерции тонкого однородного диска относительно оси, проходящей через его центр масс и лежащей в плоскости диска.