Раздел 2. Генетические параметры селекции

С начала приручения животных человек стремился улучшить хозяйственно-полезные признаки животных. Навыки, сложившиеся за это время, легли в основу целой науки – селекции сельскохозяйственных животных.

Селекция – это наука, разрабатывающая теорию и методы создания новых и совершенствование существующих пород сельскохозяйственных животных.

Теоретической основой селекции является популяционная генетика, которая изучает генетическую структуру и генетические процессы, происходящие в популяции.

Под популяцией в животноводстве понимают группу животных одной породы, размножающуюся путем чистопородного разведения или скрещивания (под контролем человека), и обладающей определенным фенотипическим и генотипическим разнообразием. Популяция может находиться на разных уровнях, начиная от породы и заканчивая отдельным стадом или линией.

Важное место в популяционной генетике принадлежит генетике количественных признаков, так как селекция в животноводстве ведется в основном по количественным признакам. Статистический или биометрический метод обработки данных является основным в популяционной генетике.

Математически обоснованные селекционные показатели, определяющие и уточняющие генетическую сущность отбора животных и признаков, по которым он ведется, получили название генетических параметров селекции.

Знание селеционно-генетических параметров необходимо для успешного проведения селекционной работы в стадах, для прогнозирования результатов селекции. Однако следует помнить, что генетические параметры признаков не постоянны и варьируют по величине, как при определении их в разных стадах, так и в одном стаде, но в разные годы. На величину генетических параметров оказывают влияние способ их оценки, число особей в анализируемой популяции, условия кормления и содержания животных и некоторые другие факторы.

Тема 1: Основные селекционно-генетические параметры

Цель: овладеть методикой расчетов генетических параметров селекции; научиться анализировать и использовать их в селекционной работе.

Методические указания. Для характеристики и оценки продуктивных признаков животных определенной популяции, а также прогнозирования результатов селекции, используются следующие селекционно-генетические параметры: среднее значение признака , показатели изменчивости (σ – среднее квадратическое или стандартное отклонение; C_v – коэффициент вариации), коэффициенты наследуемости h², корреляции r, регрессии R, повторяемости r_w, ошибки статистических величин ± m, достоверность полученных результатов t_d и Р, селекционная граница C_гр, селекционный дифференциал Sd, эффект селекции Se.

Величина среднего значения признака . Существуют следующие средние величины: средняя арифметическая, средняя геометрическая, средняя гармоническая, средняя квадратическая, мода, медиана. Средняя арифметическая является наиболее распространенным видом средних величин. Она выявляет среднее значение изучаемого признака в популяции при его варьировании. Количество особей в популяции n может быть различно. Из многочисленной популяций или генеральной совокупности обычно проводят выбор типичных особей или выборочную совокупность, которая должна достаточно полно отражать черты генеральной совокупности, т.е. быть репрезентативной. Выборка может быть большой ( ) и малой ( ).

Вычисление статистических показателей для выборки с малым числом наблюдений не представляет особой сложности (см. Меркурьева Е.К, Шангин-Березовский Г.Н., 1983; Коростелева Н.И., Рабинович И.Е., 1992).

Поскольку на практике чаще всего работают с большими стадами животных, рассмотрим подробно вычисление статистических показателей для выборки с большим числом наблюдений.

Для вычисления средней арифметической большой выборки строится вариационный ряд, и используется для расчета следующая формула:

= А + b × k, (1)

где А – условная средняя, вычисляется путем суммирования

нижней границы нулевого класса и половины классового

промежутка;

b – поправочный коэффициент;

k – классовый промежуток.

При этом b = , (2)

k = , (3)

где Р – частота класса;

а – условное отклонение от среднего класса;

n – величина выборки;

Х_max , Х _min – максимальное и минимальное значение

признака в выборке.

Число классов определяется исходя из объема выборки, например, при 60 < n < 100 удобным считается 7-11 классов.

Средняя арифметическая дает суммарную оценку любого признака, она служит центром распределения особей в выборке или популяции. При ведении племенной работы разные породы, линии, стада сравниваются, прежде всего, по уровню развития селекционируемого признака, величину которого и отражает среднее арифметическое значение.

Статистические ошибки. Однако полного совпадения выборочных данных с данными обработки генеральной совокупности, как правило, не бывает. Расхождение между величиной средней арифметической выборки и величиной средней арифметической генеральной совокупности принято называть ошибкой репрезентативности, т.е. ошибкой, допускаемой не в самом процессе измерительной и вычислительной работы, а в результате случайного отбора вариант из генеральной совокупности при образовании выборки. Это не техническая, а статистическая ошибка.

Ошибка средней арифметической большой выборки рассчитывается по формуле:

= ± , (4)

где σ – среднее квадратическое отклонение.

Принято записывать среднюю арифметическую вместе с её ошибкой в виде . Ошибка как и среднее квадратическое отклонение имеет два знака: плюс и минус, так как она в равной мере характеризует отклонение выборочной средней от средней генеральной совокупности как в сторону бόльших, так и в сторону меньших значений.

На величину статистических ошибок оказывают влияние объём выборки n и изменчивость признака σ. Чем меньше изменчивость признака и больше объем выборки, тем меньше величина статистической ошибки.

Для других параметров селекции также рассчитываются статистические ошибки, формулы которых приведены ниже. Ошибки являются величинами именованными и измеряются в тех же единицах, что и признаки. Записывают их рядом с показателем, например:

± ; σ ± m _σ; C_v ± m _Cv; r ± m_r .

Показатели изменчивости признака. Среднее квадратическое отклонение σ характеризует изменчивость признака и показывает, на сколько в среднем каждая варианта отклоняется от средней арифметической. Среднее квадратическое или стандартное отклонение для большой выборки рассчитывается по формуле:

σ = k σ = . (5)

Следует обратить внимание, что стандартное отклонение с учетом классового промежутка k называется абсолютным, без классового промежутка – относительным. Первое используется для определения статистических ошибок , m _σ, коэффициентов вариации C_v и регрессии R, второе – при расчете коэффициента корреляции r.

Ошибка среднего квадратического отклонения m_σ рассчитывается по формуле:

m _σ = ± . (6)

Среднее квадратическое отклонение служит мерой статистической изменчивости признака в стадах или других популяциях сельскохозяйственных животных. Неравномерность развития селекционного признака у особей, его изменчивость являются условиями успешного ведения племенной работы в анализируемой популяции. Большинство хозяйственно-полезных признаков характеризуются высокой степенью изменчивости. Это связано с тем, что признаки обладают сложной наследственной обусловленностью. Однако среднее квадратическое отклонение является величиной именованной, что затрудняет анализ и сопоставление изменчивости разных хозяйственно-полезных признаков в популяции.

Для сравнения изменчивости нескольких признаков, измеренных в различных единицах, используется относительная величина – коэффициент вариации C_v, выраженный в процентах:

C_v = . (7)

По величине среднего квадратического отклонения и коэффициента вариации можно судить о пластичности признака и степени гомо- или гетерозиготности популяции по анализируемому хозяйственно-полезному признаку. Если стадо генетически однородно, хорошо отселекционировано по ряду хозяйственно-полезных признаков, то значение среднего квадратического отклонения и коэффициента вариации будет невелико. В таком стаде, например, коэффициент вариации удоя составит в среднем 15-18%. Если же стадо получено путем скрещивания или в стаде используются производители с различным генетическим потенциалом продуктивности, то коэффициент вариации удоя примет значение от 30 до 50% и выше. Однако эффективность селекции тем выше, чем выше вариабельность (изменчивость), поскольку при высокой амплитуде изменчивости хозяйственно-полезных признаков имеется больше материала для отбора.

Ошибка коэффициента вариации m _Cv рассчитывается по формуле:

m _Cv = ± . (8)

Критерий достоверности t_d. Статистическая ошибка дает представление о том, в каких пределах изменчивости находится признак, но по ней нельзя судить о достоверности результатов, полученных при анализе выборочной совокупности. О достоверности полученных результатов можно судить, лишь рассчитав критерий достоверности. Критерий достоверности – величина именованная, которая рассчитывается как отношение средней величины показателя к ее ошибке:

t = . (9)

Рассчитанное значение критерия достоверности сопоставляется с табличным значением (табл. 1) в зависимости от числа степеней свободы ν, которое рассчитывается по формуле:

ν = n – 1. (10)

При сравнении средних значений между группами животных необходимо знать, достоверна ли полученная разница или она случайна. В этом случае рассчитывается критерий достоверности разницы по следующей формуле:

t_d = , (11)

где – среднее значение признака в сравниваемых группах.

Несколько иначе рассчитывается и число степеней свободы:

ν = (n₁ + n₂) – 2 , (12)

где n₁ и n₂ – количество животных в сравниваемых группах.

Затем с учетом степеней свободы рассчитанный критерий достоверности сопоставляется с табличным значением (табл. 8), и находится уровень вероятности достоверности разницы Р.

Таблица 8

Значение критерия достоверности Стьюдента-Фишера

Число степеней свободы ν	Уровень вероятности Р				Число степеней свободы ν	Уровень вероятности Р
	0,95	0,99		0,999		0,95	0,99		0,999
1	12,71		63,66	637	18	2,10	2,88	3,92
2	4,30		9,92	31,60	19	2,09	2,86	3,88
3	3,18		5,84	12,94	20	2,09	2,85	3,85
4	2,78		4,60	8,61	21	2,08	2,83	3,82
5	2,57		4,03	6,86	22	2,07	2,82	3,79
6	2,45		3,71	5,96	23	2,07	2,81	3,77
7	2,37		3,50	5,41	24	2,06	2,80	3,75
8	2,31		3,36	5,04	25	2,06	2,79	3,73
9	2,26		3,25	4,78	26	2,06	2,78	3,71
10	2,23		3,17	4,59	27	2,05	2,77	3,69
11	2,20		3,11	4,44	28	2,05	2,76	3,67
12	2,18		3,06	4,32	29	2,05	2,76	3,66
13	2,16		3,01	4,22	30-34	2,04	2,75	3,65
14	2,15		2,98	4,14	35-39	2,03	2,72	3,59
15	2,13		2,95	4,07	40-44	2,02	2,70	3,55
16	2,12		2,92	4,02	45-69	2,01	2,66	3,50
17	2,11		2,90	3,97	70-119	1,98	2,63	3,39
-	-		-	-	120 и более	1,96	2,58	3,29

Если вычисленное значение t_d будет меньше табличного при самом низком уровне вероятности (Р = 0,95), то выборочный параметр (средняя) недостоверен, то есть он не может служить характеристикой генеральной совокупности, и в этом случае полученные данные в опыте не имеют ценности, так как выводы не могут быть распространены на генеральную совокупность, изучение которой служит основной целью опыта, построенного на выборочном методе. Чаще всего недостоверность полученной величины связана с недостаточным объёмом выборки. В таких случаях необходимо увеличить число наблюдений в выборке и заново ставить опыт.

Если вычисленное значение t_d будет больше табличного, например, при Р > 0,99, значит с вероятностью 99 из 100% можно утверждать, что средняя величина исследуемой генеральной совокупности лежит в интервале .

Чем больше критерий достоверности, тем выше уровень вероятности.

Если рассчитанный критерий достоверности разности между средними величинами больше табличного при любом уровне вероятности, то отмечают, что влияние фактора (возраст, происхождение, тип кормления), по которому отличаются сравниваемые группы, достоверно. Например, удой коров третьей лактации может превосходить удой коров-первотелок на 470 кг при Р > 0,999. Значит выявлено влияние возраста на уровень удоев в сравниваемых выборках.

Показатели взаимосвязи признаков. Между биологическими признаками существует определенная связь, и эту связь называют корреляцией. Особенность этой связи состоит в том, что определенному значению одного признака соответствует не один, а несколько различных значений другого признака, варьирующих около своей средней величины. Степень взаимосвязи между признаками определяют с помощью коэффициента корреляции r, а абсолютную величину изменчивости одного признака в зависимости от другого – с помощью коэффициента регрессии R.

Коэффициент корреляции r показывает, в какой степени два признака связаны друг с другом, и в какой мере изменение одного из них влияет на изменение другого. Применение закона корреляции дает возможность при отборе по одному признаку оказывать влияние на изменение другого.

Изучение зависимости между признаками имеет большое значение для генетического совершенствования стада, так как отбор по одному признаку дает возможность предсказать изменение, которое наступит в генетической структуре популяции с другим признаком из-за связи между ними.

Корреляция может быть положительной и отрицательной. Если при увеличении одного признака значение другого (взаимосвязанного с ним) увеличивается, то имеет место положительная корреляция. Например, отбор коров по удою ведет одновременно к увеличению количества молочного жира. Чем выше положительная корреляция между признаками, тем успешнее их используют при отборе. Отрицательная корреляция наблюдается в том случае, если при уменьшении одного из признаков значение другого увеличивается. Например, при увеличении количества поросят в гнезде, уменьшается живая масса каждого поросенка. При отрицательной взаимосвязи между признаками требуется длительная одновременная селекция по обоим признакам, чтобы постепенно изменить отрицательную корреляцию между ними на положительную. Например, продуманный отбор и подбор по признакам с отрицательной взаимосвязью – молочность и жирномолочность – может стать эффективным и изменить направление взаимосвязи.

Некоторые признаки коррелируют с другими непрямолинейно, то есть с увеличением одного, возрастает и другой до определенного уровня, после чего увеличение первоначального признака в меньшей степени влечет за собой изменение в ту же сторону другого, а затем взаимосвязь данных признаков может стать отрицательной. Например, такой характер корреляции может наблюдаться между величиной удоя и живой массой, между продолжительностью сухостойного периода и удоем коров.

Принято считать связь:

слабой, если 0,10 < r < 0,30;

средней, если 0,31 < r < 0,60;

сильной, если r > 0,61.

Расчет коэффициента корреляции при большом числе наблюдений

(n > 30) проводится по формуле:

r = , (13)

где Р – частота;

а – условное отклонение;

b – поправочный коэффициент;

σ – среднее квадратическое отклонение (относительное, то есть

без классового промежутка);

n – объем выборки (количество пар признака).

При этом:

b_x = , b_y = . (14)

Коэффициент корреляции также имеет ошибку m_r, которая определяется по следующей формуле:

m_r = . (15)

Для вычисления коэффициента корреляции необходимо построение корреляционной решетки. Расчет и построение классов в корреляционной решетке проводится таким же образом, что и при работе с вариационным рядом, с той лишь разницей, что решетка объединяет сразу два вариационных ряда, один из которых располагается по вертикали, а другой – по горизонтали.

Коэффициент корреляции, отражая уровень и направление связи между признаками, не указывает, на какую величину изменяется один признак при изменении другого, взаимосвязанного с ним. Поэтому в селекции животных для количественной оценки взаимосвязи между признаками часто используется коэффициент регрессии R, который указывает величину изменения одного признака в зависимости от изменения другого (сопряженного с ним) на единицу. Коэффициент регрессии рассчитывается по формулам:

R_x/y = ± r ; R_y/x = ± r . (16)

Например, взаимосвязь признаков удоя X и жирномолочности Y в стаде коров отрицательная и составляет r = - 0,31; среднее квадратическое отклонение по удою равно 646,7 кг, а по жирномолочности – 0,17%. Подставляя значения в формулу (16), рассчитаем коэффициент регрессии:

R_x/y = R_y/x = .

Это значит, что в данном стаде при отрицательной взаимосвязи удоя и жирномолочности повышение удоя коров на 100 кг повлечет снижение жирномолочности на 0,081%, а при повышении жирномолочности на 1% удой снизится на 1179 кг.

Коэффициент наследуемости h². Племенной отбор находится в прямой зависимости от действия аддитивных генов, оказывающих непосредственное влияние на корреляцию между родственными животными и на эффективность самого отбора при массовой селекции, т.е. по фенотипу. Селекционеру важно знать величину наследуемости хозяйственно-полезных признаков, чтобы более правильно построить программу селекции. Для определения эффективности селекции в стаде, линии или породе в целом используется коэффициент наследуемости, который выражает долю генетической изменчивости в общей фенотипической изменчивости признака. То есть по его величине определяют долю влияния генотипа на проявление признака, его изменчивость в конкретной популяции. С помощью коэффициента наследуемости можно прогнозировать селекционную ценность особей по их фенотипу. По коэффициенту наследуемости, вычисленному для определенного стада, можно приблизительно рассчитать, на какую в среднем величину произойдет увеличение продуктивности в сменившемся поколении. Следует отметить, что коэффициент наследуемости рассчитывается для каждого конкретного стада, так как его величина зависит от породной принадлежности, генетической структуры стада, уровня и направления племенной работы, методов разведения, кормления и содержания, других факторов.

Коэффициент наследуемости может принимать значение от 0 до 1, а также выражаться в процентах. Чем выше генетическое разнообразие в популяции, тем выше коэффициент наследуемости, тем эффективнее будет отбор по фенотипу. В племенных стадах, где на протяжении ряда лет проводилась целенаправленная селекционная работа по улучшению основных хозяйственно-полезных признаков, генетическое разнообразие популяций обычно снижено, следовательно, показатель наследуемости – коэффициент наследуемости будет несколько ниже, чем в неотселекционированных стадах. При низком и нулевом значении коэффициента наследуемости отбор потомков по фенотипу родителей будет малорезультативным. В таких случаях племенная работа должна основываться на индивидуальном отборе и подборе пар с учетом их сочетаемости, использовании препотентных производителей, оцененных улучшателями по качеству потомства на популяциях с более высоким уровнем продуктивности. Наследуемость признаков в зависимости от величины коэффициента наследуемости может быть:

низкой, при h² < 0,30;

средней, при 0,31 < h² < 0,6;

высокой, при h² > 0,61.

Признаки с низким коэффициентом наследуемости в большей степени подвергаются инбредной депрессии, но по ним сильнее выражен эффект гетерозиса при скрещивании, так как они обладают специфической комбинационной способностью. Чем выше коэффициент наследуемости признака, тем в большей степени изменчивость их определяется наследственными различиями и тем эффективнее массовый отбор по этим признакам.

Существуют различные способы вычисления коэффициента наследуемости. Первый способ:

h² = 2 r. (17)

Коэффициент наследуемости равен удвоенному коэффициенту корреляции одного и того же признака родителей и потомков. Если признак ограничен полом, то коэффициент наследуемости выражается удвоенным коэффициентом корреляции между продуктивностью матерей и дочерей. Иногда удвоение коэффициента корреляции приводит к завышению коэффициента наследуемости и выражается величиной, превышающей единицу. В этом случае за коэффициент наследуемости можно брать коэффициент корреляции без удвоения, то есть h = r (по Рузскому С.А.).

Второй способ:

h² = 2R . (18)

Коэффициент наследуемости равен удвоенному коэффициенту регрессии между показателями признака родителей и потомства (по Д. Лашу). Этой формулой пользуются в том случае, если среди матерей проводился жесткий отбор, а дочери используются все.

Третий способ:

h² = 4 r . (19)

Коэффициент наследуемости равен учетверенному коэффициенту корреляции между показателями продуктивности полусибсов по отцу или матери.

Четвертый способ:

h² = . (20)

Коэффициент наследуемости определяется как отношение показателя дисперсии, вызываемой генетическими факторами С_X к общей фенотипической дисперсией С_Y.

Пятый способ:

h² = , (21)

где Х_Дл , Х_Дх – средние показатели признака у дочерей, полученных

от лучших л и худших х матерей (по сравнению

со средним значением по стаду);

Х_Мл , Х_Мх – средние показатели признака лучших л и худших х

матерей (по сравнению со средним значением) по стаду.

Наиболее употребляемые способы расчета коэффициента наследуемости два из них: первый и четвертый.

Коэффициент повторяемости r_w. Кроме коэффициента наследуемости мерой степени генетической обусловленности признака является коэффициент повторяемости. Если при определении коэффициента наследуемости генетическая изменчивость оценивается по сходству близкородственных особей, то вычисление коэффициента повторяемости основывается на сходстве повторных измерений продуктивности у одних и тех же особей.

Под повторяемостью признака следует понимать степень соответствия оценок по нему, проведенных в разное время. Например, между удоем коровы за первую лактацию и последующие лактации; живой массой животного в раннем возрасте и живой массой во взрослом состоянии, удоем за первые 90, 180 дней и 305 дней первой лактации.

Использование коэффициента повторяемости основано на том, что генотип животного не меняется за время жизни особи, но если наблюдать за изменением продуктивности у одного и того же животного, например, за лактацией у коровы, то заметим, что показатели продуктивности под действием факторов среды не будут постоянны. Чем больше изменчивость, вызванная факторами среды, тем ниже значение коэффициента повторяемости. Более высокие степени повторяемости наблюдаются по морфологическим признакам и некоторым качественным показателям, менее высокие – по количественным признакам.

Для более эффективной селекции особое значение имеет постоянство величин селекционируемого признака в различные промежутки времени. Поэтому степень повторяемости имеет большое значение для отбора, и чем она выше, тем надежнее отбор по первым оценкам, тем раньше можно определить племенную ценность животного, прогнозировать эффект селекции.

Одним из методов ранней оценки производителей является прогнозирование продуктивности их потомства за укороченную или полную первую лактацию. Исследованиями А.С. Всяких (1973), Б.П. Завертяева (1976) и другими установлена высокая повторяемость рангов по удою, содержанию жира и белка в молоке за первые 90 дней с этим же показателем за 305 дней лактации. Высокая степень повторяемости генетической оценки позволяет достоверно выявить улучшателей и ухудшателей по предварительным результатам за укороченное время первой лактации. Поэтому при селекции молочного скота целесообразно использовать в хозяйствах метод ранней оценки животных.

Наиболее простым является метод вычисления коэффициента повторяемости через коэффициент корреляции между последовательными изменениями признака, взятыми в разные возрастные периоды, сезоны, т.е.:

r_w = r . (22)

Коэффициент повторяемости измеряется в пределах от 0 до 1, т. е. величина положительная. Чем больше его величина приближается к единице, тем точнее оценка и эффективнее отбор по этим признакам. Другими словами, коэффициент повторяемости измеряет степень постоянства проявления признака во времени и может служить критерием при раннем отборе животных. Чем выше его величина, тем надежнее оценка и при последующих измерениях. Если бы последовательные измерения показателей продуктивности животного не отличались друг от друга, повторяемость была бы равна единице.

Пример. На основании показателей молочной продуктивности коров красной степной породы (n = 100, удой за первые 100, 200 и 305 дней первой лактации, % жира в молоке, количество килограммов молочного жира, живая масса), представленные в таблице 9, рассчитаем:

• среднюю арифметическую, среднее квадратическое отклонение, коэффициент вариации и ошибку средней арифметической по показателям молочной продуктивности (удою за 305 дней лактации, жирности молока, количеству молочного жира) и живой массе коров каждого поколения;

• коэффициент корреляции и регрессии между удоем за 305 дней лактации и жирномолочностью (%), количеством молочного жира (кг), живой массой (кг);

• коэффициенты наследуемости удоя коров за 305 дней лактации и жирномолочности через удвоенный коэффициент корреляции «мать – дочь»;

• коэффициент повторяемости удоя коров за первые 100 и 305 дней первой лактации.

Затем проанализируем полученные результаты и сделаем выводы.

Таблица 9

Показатели продуктивности за 1 лактацию и живой массы коров

исследуемой выборки

	Дочери					Матери
	удой за 305 дн., кг	жир за 305 дн., %	мол. жир за 305 дн., кг	живая масса, кг		удой, кг			жир за 305 дн., %	мол. жир за 305 дн., кг
						за 100 дн.	за 200 дн.	за 305 дн.
1	3932	3,65	144	400	1	1145	2213	3473	3,73	130
2	4278	3,62	155	430	2	1370	2541	3284	3,70	122
3	5061	3,85	195	430	3	1778	3309	4129	3,50	145
4	4509	3,69	166	410	4	1603	3076	3962	3,92	156
5	4161	3,79	158	420	5	1147	2186	3241	3,91	127
6	4134	4,45	184	430	6	1696	3065	4245	3,75	159
7	3801	3,99	152	420	7	1481	3080	3635	4,09	149
8	5140	3,41	175	432	8	1323	2491	3795	3,85	146
9	4381	4,42	194	440	9	1601	3014	4382	4,26	187
10	5238	3,28	172	435	10	1507	2981	3743	3,79	142
11	3152	3,53	111	390	11	1664	3119	3556	3,97	141
12	3747	4,32	162	400	12	1343	2667	3924	3,67	144
13	4448	3,63	161	430	13	1825	2756	2895	4,90	142
14	4273	3,71	159	460	14	1282	2287	3340	3,52	118
15	4518	3,98	180	428	15	1204	2396	3457	3,64	126
16	4627	4,10	190	410	16	1023	2098	3300	3,61	119
17	3807	4,16	158	470	17	1453	2910	3984	3,70	148
18	4876	3,77	184	427	18	1453	2910	3984	3,70	148
19	3294	3,93	129	400	19	1114	2156	3235	3,62	117
20	5322	3,86	205	430	20	1529	3080	4288	3,49	150
21	4268	3,66	156	410	21	1489	2812	3778	3,5	132
22	5760	3,87	223	420	22	1484	2490	3310	3,75	124
23	4961	3,84	190	420	23	1670	3026	4161	3,58	149
24	4494	4,49	202	420	24	1561	3091	4326	3,81	165
25	4070	4,51	183	432	25	1709	3050	4016	3,66	147
26	3532	4,00	141	428	26	1552	2476	3445	3,71	128
27	4881	3,65	178	415	27	1184	2516	3319	4,24	141
28	4731	3,42	162	430	28	1861	3215	4174	3,74	156
29	4377	3,53	155	400	29	1537	2743	3962	3,42	136
30	5189	3,95	205	415	30	1378	2446	3036	3,49	106
31	4077	3,49	142	400	31	1512	2900	3834	3,57	137
32	4764	3,91	186	403	32	1330	2309	3004	3,91	117
33	3970	4,06	161	420	33	1312	2339	3208	3,93	126
34	4521	3,62	164	410	34	1438	2584	3180	3,61	115
35	3342	3,64	122	420	35	1438	2584	3180	3,61	115
36	6059	3,28	199	430	36	1382	2381	3045	3,71	113
37	5341	3,68	197	425	37	1352	2484	3348	3,63	121
38	4086	4,12	169	415	38	1437	2766	3670	3,80	140
39	4890	3,94	193	430	39	1433	2284	2966	3,71	110
40	4326	3,72	161	440	40	1782	3395	4410	3,70	163

Для определения среднего арифметического значения в популяции с большим количеством особей необходимо построить вариационный ряд по каждому селекционируемому признаку, например, по удою (табл. 10).

Построение вариационного ряда следует начать с определения:

• максимального и минимального значения признака:

Х_max = 6059 кг, Х_min = 3152 кг;

• разницы между ними:

Х_max – Х_min = 6059 – 3152 = 2907 кг;

• числа классов вариационного ряда, например:

при 40 < n < 60 – 6-8 классов

при 60 < n < 100 – 7-10 классов.

• величины классового промежутка – k:

k = = 582 кг;

• нижней и верхней границ каждого класса:

1-й класс: Х_min = 3152

Х_max = (Х_min + k) – 1 = 3152 + 582 – 1 = 3733;

2-й класс: 3152 + k = 3734

3734 + 582 – 1 = 4315;

3-й класс: 3734 + 582 = 4316

4316 + 582 – 1 = 4897 и так далее.

• частот каждого класса, пользуясь десятичной системой квадратов, при этом сумма частот классов 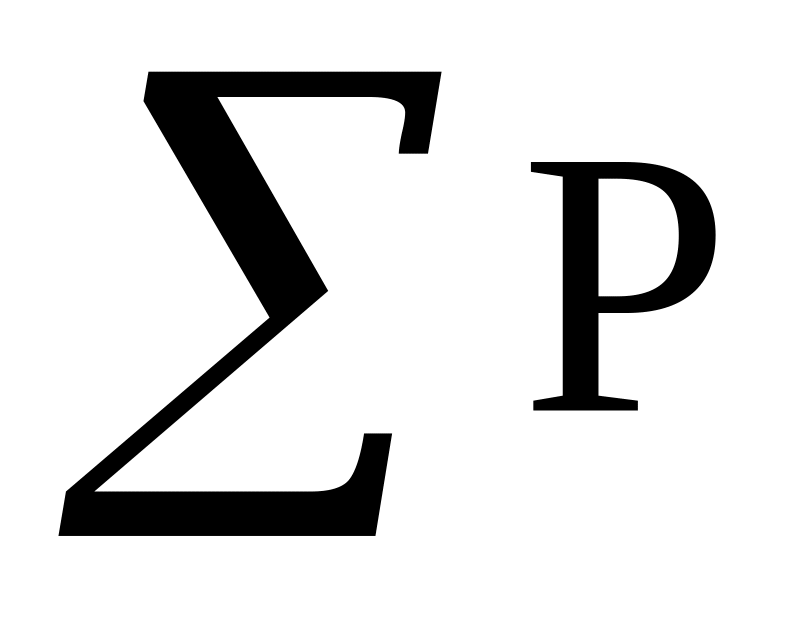должна соответствовать величине выборки n;

• среднего или «нулевого» класса (класса с самой высокой частотой) и условного отклонения для каждого класса;

• для каждого класса значений Р × а и Р × а², затем суммы этих значений, то есть 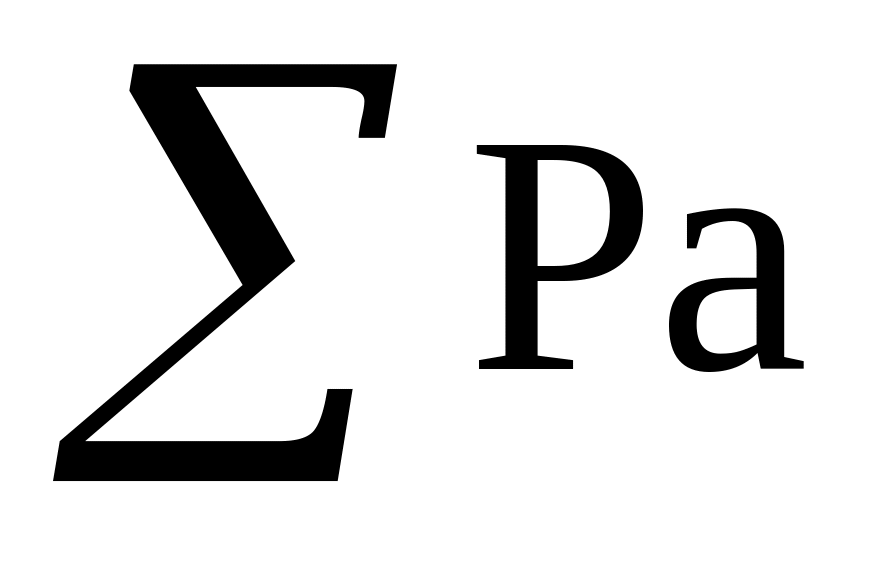и .

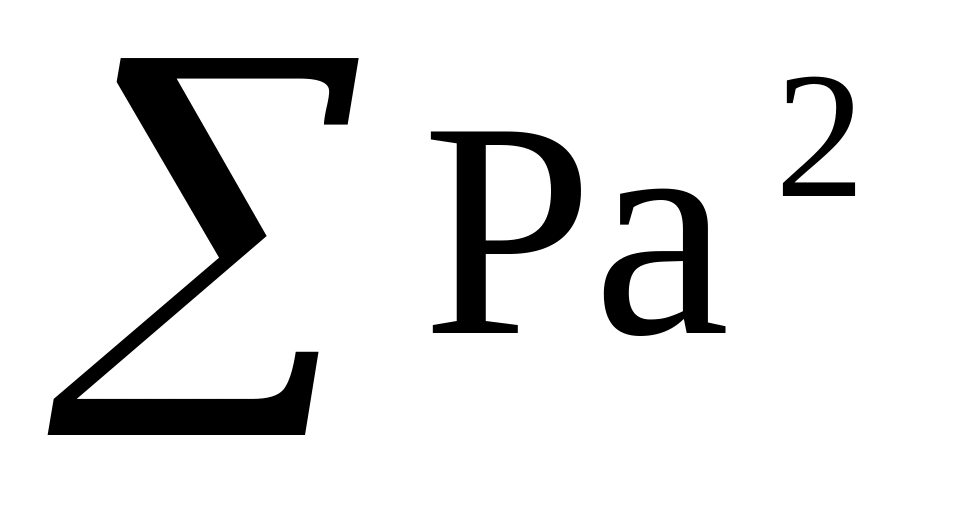Данные значения необходимы для расчета средней арифметической и показателей изменчивости признака.

Таблица 10

Вариационный ряд удоя дочерей Хеликона 837

за 305 дней первой лактации

№ класса	Границы класса	Частота класса Р	Условное отклонение а	Р × а	Р × а2
1	3152-3733	4	– 2	– 8	16
2	3734-4315	13	– 1	– 13	13
3	4316-4897	14	0	0	0
4	4898-5479	7	1	7	7
5	5480-6051	2	2	4	8
	Сумма	40	×	- 10	44

Исходя из построения вариационного ряда среднее арифметическое значение удоя составляет:

= А + b × k = 4607 + (– 0,25 × 582) = 4461,5 кг,

где А = 4316 + = 4607 кг;

b = = = – 0,25.

Затем следует рассчитать показатели изменчивости признака (абсолютное стандартное отклонение, коэффициент вариации) и статистическую ошибку среднего арифметического, пользуясь приведенными выше формулами (4, 5, 6, 7, 8) и данными таблицы 10:

σ = ± 582 = ± 592,8 кг , C_v = = 13,3%,

m _σ = ± = 66,3кг , m _Cv = ± = 1,5% ,

= ± кг.

Рассмотрев пример расчетов такого признака, как удой дочерей производителя, аналогично проведем расчеты по другим признакам, в том числе в группе коров-матерей. Для более удобного анализа все полученные результаты формируются в таблицу 11. Так, на практике важно освоить не только приемы расчетов, но и уметь анализировать полученные данные, сопоставляя их с уже имеющимися цифрами. Проводить сравнение можно с показателями прошлых лет, достигнутыми в хозяйстве, районе, крае, с показателями племенных хозяйств, со стандартными требованиями по породе.

Таблица 11

Показатели хозяйственно-полезных признаков коров по 1-й лактации

Признак		Показатель
		дочерей	матерей	стандарта породы	по хозяйству	по краю (красн. степ.)
Удой, кг	σ Cv, %	4461,5 ± 93,7 592,8 13,3	3630,6 ± 70,5 445,8 12,3	2400	4326	3023,0
Жирность, %	σ Cv, %	3,83 ± 0,05 0,31 8,3	3,75 ± 0,04 0,26 7,1	3,70	3,89	3,95
Молочный жир, кг	σ Cv, %	172,5 ± 3,9 24,6 14,3	136,4 ± 2,8 17,6 12,9	89	168	119,4
Живая масса, кг	σ Cv, %	421,9 ± 2,5 15,9 3,8	-	390	419	400

Анализируя продуктивность и живую массу животных разных поколений, следует отметить, что удой, жирность молока, а, следовательно, и количество молочного жира выше у дочерей. Их превосходство по признакам составляет соответственно 831 кг, 0,08% и 36 кг. Кроме того, все показатели дочерей превышают стандартные требования красной степной породы. При сравнении с показателями, достигнутыми в хозяйстве и крае, дочери уступают по жирномолочности, но за счет более высокого удоя, превосходят по количеству молочного жира, а также по живой массе. Сравнение изменчивости разных признаков (по величине коэффициента вариации) показывает, что как в группе дочерей, так и в группе матерей наиболее вариабельными являются удой и количество молочного жира, а наименее – живая масса. Величина среднего квадратического отклонения позволяет определить изменчивость одноименных признаков. Например, изменчивость удоя в группе дочерей выше на 147,0 кг, это значит, что среди них можно отобрать больше особей с желаемым удоем.

Ранее отмечалось, что при сравнении показателей разных групп селекционеру важно знать достоверно ли превосходство средней величины одной группы над другой по каждому из признаков, или это случайно полученная разница, поскольку средняя величина признака в каждой группе находится в пределах своей ошибки. Для этого проводят расчет критерия достоверности полученной величины и критерия разности двух средних величин. Но поскольку при анализе большой выборки полученные значения практически всегда достоверны, то наиболее важно определить достоверность разницы между средними арифметическими в сравниваемых группах.

Например, удой дочерей выше удоя матерей на 831 кг, но с учетом статистических ошибок удой дочерей в генеральной совокупности может находиться в пределах от 4555,2 до 4367,8 кг, а удой матерей от 3701,1 до 3560,1 кг. Соответственно различия составляют от 667 до 995 кг. Возникает вопрос: существенно ли это превосходство, влияние ли это отца на дочерей или случайное явление.

По приведенным выше формулам (11, 12) рассчитаем величины критерия достоверности разности между средними величинами и степени свободы. Для того, чтобы величина критерия достоверности не принимала отрицательное значение, принято в числителе из большей средней арифметической вычитать меньшую:

t_d = = 7,09 ; ν = (40 + 40) – 2 = 78

Пользуясь таблицей 8, определяем, что величина критерия достоверности 7,09 при числе степени свободы 78 соответствует самому высокому уровню вероятности (Р > 0,999), поскольку 7,09 > 3,39.

Аналогично определяем критерий достоверности разности по другим признакам между группами дочерей и матерей. Так по жирномолочности t_d = 1,15. Это значение ниже табличного при самом низком уровне вероятности (Р > 0,95). По количеству молочного жира t_d = 7,53; что выше табличного при Р > 0,999.

Таким образом, расчет критерия достоверности разницы средних арифметических показал, что превосходство дочерей над матерями по удою и количеству молочного жира достоверно, т.е. увеличение этих признаков в поколении дочерей обусловлено влиянием отца (поскольку не известно, чем еще отличались сравниваемые группы). А различия по жирномолочности на 0,08% получены случайно.

В селекции животных важно знать не только уровень развития каждого признака, но и уровень взаимосвязи между ними, поскольку обычно селекция ведется сразу по двум-трем признакам. Учитывая, что на проявление количественных признаков влияют как среда, так и наследственность, селекционеру необходимо знать долю их влияния, которая определяется путем расчета коэффициентов наследуемости и повторяемости селекционируемых признаков.

Используя данные таблицы 9, определим взаимосвязь между такими признаками, как удой Y и количество молочного жира X. Для этого следует построить корреляционную решетку, которая состоит из вариационных рядов этих признаков (табл. 12). Методика построения вариационного ряда приведена выше, следует отметить лишь, что количество классов в каждом ряду должно быть одинаковым.

Таблица 12

Корреляционная решетка

Y	X					Рy			ay		Рy × ay		Рy × ay2
	111 – 133	134 – 156	157 – 179	180 – 202	203 – 225
3152 – 3733	3	1					4	– 2			- 8		16
3734 – 4315		5	6	2			13	– 1			- 13		13
4316 – 4897		1	6	7			14	0			0		0
4898 – 5479			2	3	2		7	1			7		7
5480 – 6061				1	1		2	2			4		8
Px	3	7	14	13	3		40				= = – 10		= = 44
ax	– 2	– 1	0	1	2
Px × ax	– 6	– 7	0	13	6
Px × ax2	12	7	0	13	12

Определив частоты Р и условные отклонения а находим и для расчета b_x и b_y (2), а затем и для расчета относительных σ_x и σ_y (5), т.е. без классового промежутка:

b_x = = 0,15 ; b_y = = – 0,25 ;

σ_x = = 1,038 ; σ_y = = 1,018 .

Далее необходимо найти выражение . Для этого определяется на какое количество квадратов делится корреляционная решетка условными средними классами (нулевыми). В этом примере – на 4 квадрата, но иногда может быть меньше. Затем в каждом квадрате определяется сумма произведений частоты Р на отклонения по X(а_x) и Y(а_y):

В первом квадрате: В третьем квадрате:

3 × (– 2) × (– 2) = 12 0

1 × (– 1) × (– 2) = 2

5 × (– 1) × (– 1) = 5

= 19

Во втором квадрате: В четвертом квадрате:

2 × 1 × (– 1) = – 2 3 × 1 × 1 = 3

2 × 2 × 1 = 4

1 × 1 × 2 = 2

1 × 2 × 2 = 4

= – 2 = 13

Далее находится общая сумма сумм квадратов:

= 19 + (– 2) + 0 + 13 = 30.

Итак, определив все составляющие формулы (13), рассчитаем величину коэффициента корреляции:

r = = 0,75 .

Аналогично проводится расчет коррелятивных связей между другими признаками. Результаты удобней представить в таблице 13.

Таблица 13

Показатели взаимосвязи между признаками

Признак	r
Удой дочерей, кг × жирность молока дочерей, %	– 0,29
Удой дочерей, кг × мол. жир дочерей, кг	0,75
Удой дочерей, кг × живая масса дочерей, кг	0,22
Удой матерей, кг × жирность молока матерей, %	– 0,20
Удой матерей, кг × мол. жир матерей, кг	0,86
Удой дочерей, кг × удой матерей, кг	– 0,13
Жирность молока дочерей, %× жирность молока матерей, %	0,16
Удой матерей за 100 дней 1-й лактации, кг × удой матерей за 305 дней 1-й лактации, кг	0,54
Удой матерей за 200 дней 1-й лактации, кг × удой матерей за 305 дней 1-й лактации, кг	0,80

Анализируя полученные коэффициенты корреляции, следует отметить, что уровень их в популяции различен. Как в группе дочерей, так и в группе матерей между удоем и жирностью молока обнаружена отрицательная, но невысокая взаимосвязь. Это значит, что с увеличением удоя жирность молока будет незначительно уменьшаться. Однако между удоем коров и количеством молочного жира наблюдается высокая положительная связь, причем в группе матерей она еще выше, чем в группе дочерей. Так, отбор коров с высоким удоем приведет к увеличению килограммов молочного жира, но при этом жирность молока несколько снизится. Подобрав к самкам производителя, оцененного как улучшатель жирномолочности, можно отрицательную связь между признаками изменить на положительную, которая более желательна при ведении селекции одновременно по нескольким признакам.

Для того, чтобы выяснить на сколько изменится один признак при изменении другого, взаимосвязанного с ним, необходимо рассчитать коэффициент регрессии (16). При этом надо помнить, что среднее квадратическое отклонение здесь абсолютное, т. е. умноженное на классовый промежуток.

Так, например, в группе дочерей регрессия составила:

• между удоем Х и жирностью молока Y:

R_x/y = ; R_y/x = ;

• между удоем Х и количеством молочного жира Y:

R_x/y = ; R_y/x = .

В первом случае отрицательная величина коэффициента регрессии обусловлена направлением корреляции между удоем и жирномолочностью коров, т. е. при увеличении удоя на 1 кг жирность молока уменьшится на 0,00015%. Для наглядности каждую величину можно умножить на одно и то же число, например, на 100. Тогда при увеличении удоя на 100 кг жирномолочность будет меньше на 0,015%. Обратный коэффициент регрессии показывает, что при увеличении жирности молока на 1% удой снизится на 554,5 кг. Если же один из признаков будет уменьшаться на единицу (измерения), другой будет увеличиваться соответственно полученной величине коэффициента регрессии.

Во втором случае при высокой положительной взаимосвязи изменение (увеличение или уменьшение) удоя на 1 кг повлечет изменение в ту же сторону молочного жира на 0,031 кг, а изменение молочного жира на 1 кг приведет к изменению удоя на 18,1 кг. При отборе по количественным признакам желательно, чтобы корреляция между ними была положительная, но нельзя допустить ухудшения условий среды, иначе потери по одному признаку (удой) приведут к потерям и по другому (молочный жир).

Расчет корреляции между родственными группами (дочери – матери) позволяет определять коэффициент наследуемости каждого признака. Используя данные таблицы 13 и формулу (17), определяем величину коэффициента наследуемости удоя и жирномолочности:

h² = 2 × 0,13 = 0,26 ; h² = 2 × 0,16 = 0,32 .

Отсюда следует, что получен низкий коэффициент наследуемости удоя, и средний – жирномолочности. Это значит, что варьирование удоя только на 26% обусловлено влиянием генотипа, а на 74% (100% – 26%) влиянием среды, тогда как жирность молока коров данной группы в меньшей степени зависит от внешних факторов (100% – 32% = 68%). Следовательно, отбор только по этому признаку быстрее приведет к желаемому результату, но при ведении селекции одновременно по жирномолочности и удою следует не забывать о невысокой отрицательной корреляции между этими признаками.

В таблице 13 представлен также расчет коэффициента корреляции между удоем матерей, полученным в разное время, то есть за первые 100, 200 и 305 дней первой лактации. По удою в эти периоды проводят раннюю оценку коров, а по величине коэффициента корреляции r судят о степени повторяемости признака r_w. Так, между удоем коров за 100 и 305 дней обнаружен коэффициент повторяемости (0,54) средней величины, а между удоем за 200 и 305 дней – высокая повторяемость признака (0,80). Таким образом, более точно прогнозировать удой коров за 305 дней лактации можно по удою за первые 200 дней, то есть в 80 случаях из ста от коров за 305 дней лактации можно получить уровень удоя аналогично уровню удоя за 200 дней. Однако величина повторяемости удоя 0,54 также достаточно высокая для того, чтобы как можно раньше прогнозировать продуктивность и назначение первотелок, но при условии, что в хозяйстве на протяжении ряда лет будут созданы хорошие условия кормления и содержания животных.