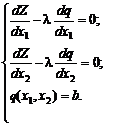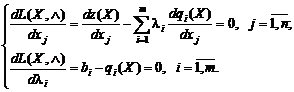8. Методы нелинейного программирования.

Нелинейное программирование ( NLP, англ. N On L inear P rogramming ) - случай математического программирования, в котором целевой функцией или ограничениями является нелинейная функция.

Задача нелинейного программирования ставится как задача нахождения оптимума определенной целевой функции   при выполнении условий

,

где   - параметры,   - ограничения, n - количество параметров, s - количество ограничений.

В отличие от задачи линейного программирования в задаче нелинейного программирования оптимум не обязательно лежит на границе области, определенной ограничениями.

 

Существуют несколько методов для решения невыпуклых задач. Один подход заключается в использовании специальных формулировок задач линейного программирования. Другой метод предусматривает использование методов ветвей и границ, где задача делится на подклассы, чтобы быть решенной с выпуклыми (задача минимизации) или линейными аппроксимациями, которые образуют нижнюю границу общей стоимости в пределах раздела. При следующих разделах в определенный момент будет получено фактическое решение, стоимость которого равна лучшей нижней границе, полученной для любого из приближенных решений. Это решение является оптимальным, хотя, возможно, не единственным. Алгоритм можно прекратить на ранней стадии, с уверенностью, что оптимальное решение находится в рамках допустимого отклонения от найденной лучшей точки; такие точки называются ? (Эпсилон)-оптимальными. Завершение у ? (Эпсилон)-оптимальных точек, как правило, необходимое для обеспечения конечности завершения. Это особенно полезно для больших, сложных задач и задач с неопределенными расходами или значениями, где неопределенность может быть определена из соответствующей оценки надежности.

Диференцийовнисть и условия регулярности, условия Каруша - Куна - Такера (ККТ) обеспечивают необходимые условия оптимальности решения. При выпуклости, эти условия являются и достаточными.

9. Метод неопределенных множителей Лагранжа.

Метод неопределенных множителей Лагранжа

Пусть задача состоит в отыскании плана X, доставляющего экстремальное значение целевой функции  max(min): Z = z(X) (5.1)  при ограничениях  qi(X) = bi, i = 1..m (5.2)  Будем считать, что функции (5.1) – (5.2) непрерывны и дважды дифференцируемые по своим аргументам. Как можно решить такую задачу условной оптимизации? Рассмотрим случай, когда число переменных равно двум и число ограничений – одному:  max(min): Z = z(x1,x2), (5.3)  q(x1,x2) = b. (5.4)  Выразим переменную x 2 в уравнении (5.4), получим выражение  x2 = φ(x1). (5.5)  Подставим его в целевую функцию (5.3). Получим  Z = z(x1, φ(x1)) (5.6)  как неявную функцию от переменной x 1. Необходимым условием существования экстремума функции (5.6), включающей исходное ограничение (5.4), является условие   (5.7)  или  . (5.8)  Продифференцируем (5.4) по x 1 как неявную функцию    Так как x2 = φ(x1), имеем   (5.9)  Подставим (5.9) в (5.8), получим   (5.10)  Обозначив   (5.11)  получим из (5.10), (5.11), (5.4) систему уравнений:

(5.12)

Система уравнений (5.12) есть необходимое условие существования условного локального экстремума задачи (5.3) – (5.4). Решив систему (5.12) с неизвестными x1, x2 и λ найдем все точки X* подозрительные на экстремум. Систему (5.12) необходимых условий определения подозрительных точек на экстремум X* можно получить формальным путем. Составим вспомогательную функцию L(X, λ)=z(x1,x2)+λ[ b- q( x1, x2)]. Она называется функцией Лагранжа, а λ – неопределенным множителем Лагранжа. Если в ней считать x1, x2 и λ независимыми переменными, найти частные производные по x1, x2 и λ и приравнять их к нулю, то получим систему (5.12).  Для задачи в общем виде (5.1) – (5.2) функция Лагранжа будет иметь вид:    где    Исходная задача (5.1) – (5.2) отыскания условного экстремума заменяется задачей отыскания безусловного экстремума функции Лагранжа L(X, λ), которая может быть решена через систему уравнений:

(5.13)(5.14)

Условия (5.13) – (5.14) необходимы для экстремума задачи (5.1) – (5.2), т.е. каждая точка X * задачи (5.1) – (5.2) является решением условий (5.13) – (5.14). Однако условия (5.13) – (5.14) не являются достаточными, т.е. не обязательно, чтобы любое решение системы (5.13) – (5.14) доставляло экстремальное значение функции (5.1).  Пример 5.1. Исследовать точки на экстремум   x 1+ x 2=1  Составим функцию Лагранжа    Составим необходимые условия существования экстремума

Решим систему уравнений  а т.к.  то   тогда  Значение целевой

Чтобы оценить, является ли точка экстремальной и какой экстремум она дает, обратимся к достаточному условию существования экстремума функции двух переменных (условию Лежандра-Клебша.  Составим определитель      Рис. 5.2 - Графическое решение  Так как   и Δ>0, то в точке X*(½; ½) функция Z достигает минимальное значение. Графическое решение (рис. 5.2) показывает, что максимальное значение Zmax=1 достигается в точках (x1=1; x2=0) и (x1=0; x2=1) Таким образом, если бы исходная задача в примере ставилась бы на отыскание максимума, то с помощью решения системы уравнений необходимых условий существования экстремума мы точку максимума бы не определили. Требуется иной подход, который рассмотрим ниже в других разделах.