8. Теорема Гаусса-Маркова. Свойства оценок мнк (определения)

Пусть матрица X уравнений наблюдений 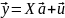имеет размер 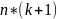, где 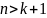, и обладает линейно-независимыми столбцами, а случайные возмущения 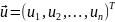удовлетворяют четырем условиям:

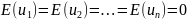
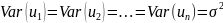
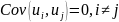
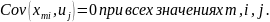
Тогда:

А) Наилучшая линейная процедура 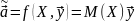имеет вид:

Б) Эффективная линейная несмещенная оценка обладает свойством наименьших квадратов:

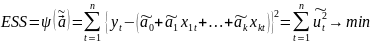
В) Ковариационная матрица оценки вычисляется по правилу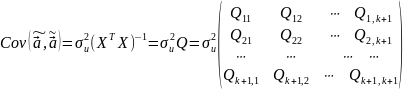

Г) Несмещенная оценка параметра 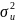модели находится по формуле

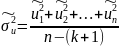
где n – число уравнений наблюдений, k+1 – количество неизвестных коэффициентов функции регрессии модели.

9. Тест Голдфелда-Квандта гомоскедастичности случайного возмущения в линейной модели множественной регрессии.

В этом случае также предполагается, что стандартное отклонение σi =σ(ε) пропорционально значению xi, т. е. σ² = σ²_ix²_i, i = 1, 2,…, n. Предполагается, что εi имеет нормальное распределение и автокорреляция остатков отсутствует. Тест Голдфелда-Квандта состоит в следующем:

1. Все n наблюдений упорядочиваем по величине X.

2. После этого всю упорядоченную выборку разбиваем на три подвыборки размерностей k, n-2k, k соответственно.

3. Оцениваем отдельные регрессии для первой подвыборки (k первых наблюдений) и для третьей подвыборки (k последних наблюдений). Если предположение о пропорциональности дисперсий отклонений значениям Xверно, то дисперсия регрессии по k первой подвыборке (сумма квадратов отклонений S₁ = Σe²_i) будет существенно меньше дисперсии регрессии по третьей подвыборке n суммы квадратов отклонений S₃ = Σe²_i).

4. Для сравнения соответствующих дисперсий строим следующую F-статистику:

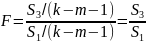
Здесь (k-m-1) число степеней свободы выборочных дисперсий (m — количество объясняющих переменных в уравнении регрессии). При сделанных предположениях относительно случайных отклонений построенная F-статистика имеет распределение Фишера с числами степеней свободы ν1 = ν2 = (k-m-1).

5. Если F_набл = S₃/S₁>F_крит = F_α,v1,v2;, то гипотеза об отсутствии гетероскедастичности отклоняется (здесь α — выбранный уровень значимости).Важный вопрос: какими должны быть размеры подвыборок для принятия обоснованных решений? Для парной регрессии Голдфелд и Квандт предлагают следующие соотношения: n = 30, k = 11; n = 60, k = 22.Для множественной регрессии данный тест, как правило, проводится для той объясняющей переменной, которая в наибольшей степени связана с σi. При этом k должно быть больше, чем (m + 1) . Если нет уверенности относительно выбора переменной X, то данный тест можно проводить для каждой из объясняющих переменных. Тест Голдфелда-Квандта может быть использован при предположении об обратной пропорциональности между σi и значениями объясняющей переменной. При этом статистика Фишера примет вид: F = S₁/S₃.

10. Эконометрика: определение, задача, цель и метод. Назначение эконометрических моделей.

Эконометрика – наука, изучающая конкретные количественные закономерности и взаимосвязи экономических объектов и процессов с помощью математических методов и моделей.

Задача эконометрики состоит в выявлении связей между количественными характеристиками экономических объектов. Целью выявления связей является построение математических правил прогноза, недоступных для наблюдения количественных характеристик изучаемых объектов по наблюденным или заданным значениям других количественных характеристик этих объектов.

Эконометрика служит инструментом решения прогнозных экономических задач методом математического моделирования.

11. Алгоритм проверки значимости коэффициентов парной регрессионной модели в Excel (с помощью функции «ЛИНЕЙН» или пакета «Анализ данных»). Доверительные интервалы параметров парной регрессионной модели (формулы расчета).

а) Алгоритм проверки значимости коэффициентов парной регрессионной модели

При проверки качества модели парной регрессии наиболее важной является задача установления линейной зависимости между эндогенной переменной и регрессом модели.

С этой целью проверяется значимость оценки параметра b.

Алгоритм проверки значимости параметра b:

б) Доверительные интервалы

Алгоритм построения:

1. Оценка параметров модели по выборочным данным

2. Оценка значений эндогенной переменной и вычисление остатков регрессии

3. Оценка дисперсии возмущений

4. Оценка дисперсии коэффициентов

5. Выбор критического (табличного значения) статистики t (n-2)

6. Вычисление границ доверительных интервалов параметров модели по формулам