Применение фиктивных переменных при исследовании сезонных колебаний: спецификация модели, экономический смысл параметров при фиктивных переменных. (15)
Термин “фиктивные переменные” используется как противоположность “значащим” переменным, показывающим уровень количественного показателя, принимающего значения из непрерывного интервала. Как правило, фиктивная переменная — это индикаторная переменная, отражающая качественную характеристику. Чаще всего применяются бинарные фиктивные переменные, принимающие два значения, 0 и 1, в зависимости от определенного условия. Например, в результате опроса группы людей 0 может означать, что опрашиваемый - мужчина, а 1 - женщина. Могут быть разного рода атрибутивные признаки, такие, например, как профессия, пол, образование, климатические условия, принадлежность к определенному региону.
Регрессионная модель, включающая в качестве фактора (факторов) фиктивную переменную, называется регрессионной моделью с переменной структурой.
Рассмотрим временной ряд Xi j,
где i — это номер сезона (периода времени внутри года, напри мер, месяца или квартала);
(L — число сезонов в году);
j
— номер года, j =
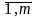(m — общее количество лет).
Количество уровней исходного ряда равно L × m = n. Число сезонных фиктивных переменных в регрессионной модели всегда должно быть на единицу меньше сезонов внутри года, т. е. должно быть равно величине L − 1. При моделировании годовых данных регрессионная модель, помимо фактора времени, должна содержать одиннадцать фиктивных компонент (12 − 1).
Каждому из сезонов соответствует определенное сочетание фиктивных переменных. Сезон, для которого значения всех фиктивных переменных равны нулю, принимается за базу сравнения. Для остальных сезонов одна из фиктивных переменных принимает значение, равное единице. Если имеются поквартальные данные, то значения фиктивных переменных D1, D2, D3 будут принимать следующие значения для каждого из кварталов
Квартал |
D2 |
D3 |
D4 |
1 |
0 |
0 |
0 |
2 |
1 |
0 |
0 |
3 |
0 |
1 |
0 |
4 |
0 |
0 |
1 |
Общий вид регрессионной модели с переменной структурой в данном случае будет иметь вид:
yt =β0 +β1 ×t+δ2 ×D2 +δ3 ×D3 +δ4 ×D4 +εt
Построенная модель регрессии является разновидностью аддитивной модели временного ряда. Базисным уравнением исследуемой регрессионной зависимости будет являться уравнение тренда для первого квартала:
y =β +β ×t+ε
Тогда общий вид модели регрессии с переменной структурой будет иметь вид:
yt=β0+ β1*t+δ2*D2+δ3*D3+δ4*D4+εt.
Данная модель регрессии представляет собой одну из разновидностей аддитивной модели временного ряда.
На основе общей модели регрессии с переменной структурой можно составить базисную модель или модель тренда для первого квартала:
yt=β0+ β1*t+εt.
Также на основе общей модели регрессии с переменной структурой можно составить частные модели регрессии:
1) частная модель регрессии для второго квартала:
yt=β0+ β1*t+δ2+εt;
2) частная модель регрессии для третьего квартала:
yt=β0+ β1*t+δ3+εt;
3) частная модель регрессии для четвёртого квартала:
yt=β0+ β1*t+δ4+εt.
Данные частные модели регрессии отличаются друг от друга только на величину свободного члена δi.
Коэффициент β1 характеризует среднее абсолютное изменение уровней временного ряда под влиянием основной тенденции.
Сезонная компонента для каждого сезона рассчитывается как разность между средним значением свободных членов всех частных моделей регрессий и значением постоянного члена одной из моделей.
Среднее значение свободных членов всех частных моделей регрессий рассчитывается по формуле:
Для поквартальных данных оценка сезонных отклонений осуществляется по формулам:
1) оценка сезонного отклонения для первого квартала:
2) оценка сезонного отклонения для второго квартала:
3) оценка сезонного отклонения для третьего квартала:
4) оценка сезонного отклонения для четвёртого квартала:
Сумма сезонных отклонений должна равняться нулю.