35. Выявление и устранение аномальных наблюдений во временных рядах.(15)

Выявление аномальных наблюдений – обязательная процедура этапа предварительного анализа данных во временных рядах. Наличие аномальных наблюдений приводит к искажению результатов моделирования. Один из методов диагностики аномальных наблюдений – метод Ирвина. Для всех или только для подозреваемых в аномальности наблюдений вычисляется величина λ_t:

,

где

Если рассчитанная величина превышает критическое значение критерия Ирвина λ (определяемое по соответствующей таблице по значениям n-число наблюдений и доверительной вероятности P), то уровень y_t считается аномальным. Аномальные наблюдения исключаются из временного ряда и заменяются их расчетными значениями (самый простой способ замены – в качестве нового значения принять среднее из двух соседних значений).

36. Измерение тесноты связи между показателями. Анализ матрицы коэффициентов парной корреляции. (15 баллов).

В зависимости от объема выборочной совокупности предлагаются различные методы оценки существен­ности линейного коэффициента корреляций.

Оценка значимости коэффициента корреляции при малых объемах выборки выполняется с использованием t-критерия Стьюдента. При этом фактическое (наблюдаемое) значение этого критерияопределяется по формуле

Вычисленное по этой формуле значение 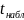сравнивается с критическим значениемt-критерия, которое берется из таблицы значений t-критерия Стьюдента с учетом заданного уровня значимости αи числа степеней свободы(n - 2).

Если t_набл>t_табл, то полученное значение коэффициента корре­ляции признается значимым (т.е. нулевая гипотеза, утвержда­ющая равенство нулю коэффициента корреляции, отвергается). И таким образом делается вывод, что между исследуемыми пере­менными есть теснаястатистическая взаимосвязь.

Если значение r_у,х близко к нулю, связь между переменными слабая. Если корреляция между случайными величинами:

• положительная, то при возрастании одной случайной ве­личины другая имеет тенденцию в среднем возрастать;

• отрицательная, то при возрастании одной случайной ве­личины другая имеет тенденцию в среднем убывать.

Для качественной оценки коэффициента корреляции применяют­ся различные шкалы, наиболее часто — шкала Чеддока. В зависи­мости от значения коэффициента корреляции связь может иметь одну из оценок:

0,1—0,3 — слабая;

0,3-0,5 — заметная;

0,5—0,7 — умеренная;

0,7—0,9 — высокая;

0,9—1,0 — весьма высокая.

Матрица коэффициентов парной корреляции

Коэффициенты парной корреляции используются для измере­ния силы линейных связей различных пар признаков из их множе­ства. Для множества признаков получают матрицу коэффициентов парной корреляции.

Пусть вся совокупность данных состоит из переменной Y= (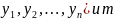 переменных (факторов)X,каждая из которых содержит n наблюдений. Значения переменных Yи X, содержа­щиеся в наблюдаемой совокупности, записываются в таблицу

На основании данных, содержащихся в этой таблице, вычисля­ют матрицу коэффициентов парной корреляции R,она симмет­рична относительно главной диагонали:

Анализ матрицы коэффициентов парной корреляции исполь­зуют при построении моделей множественной регрессии.