Задача №15

Определите устойчивость и запас устойчивости по ЛЧХ разомкнутой системы:

Заштрихованные области – это запасы устойчивости.

16.

Система автоматического регулирования имеет в разомкнутом состоянии передаточную функцию: (1) Постройте логарифмические асимптотическую амплитудную и фазовую частотные характеристики системы для коэффициента усиления .

РЕШЕНИЕ:

Частотная передаточная функция, соответствующая (1), имеет вид

Из выражения (2) или (1) видно, что асимтотическая амплитудная характеристика имеет вид ломаной прямой с участками, имеющими отрицательный наклон 20-40-20-40-60 дБ/дек, и с изломами в точках первый участок характеристики является частью прямой с наклоном -20дБ/дек, пересекающей ось частот в точке w=K.

Асимптотическая амплитудная характеристика .

Фазовая характеристика может быть найдена как сумма ординат фазовой характеристики идеального интегрирующего звена, фазовых характеристик и апериодических звеньев с постоянными времени - дифференцирующего звена с постоянной времени .

- результирующая фазовая характеристика.

17.

Передаточная функция разомкнутой следящей системы имеет вид

.

Определите первые три коэффициента ошибки, а также добротность

по скорости.

Структурная схема следящей системы

РЕШЕНИЕ:

Находим передаточную функцию относительно ошибки:

Разлагаем это выражение в ряд делением числителя на знаменатель

Далее можем написать тождество:

Отсюда получаем коэффициенты ошибок:

Добротность по скорости:

18. Определите установившуюся ошибку регулирования САУ по каналу

управления для входных сигналов:

1. u(t)=101(t);

2. u(t)=10t, если .

Структурная схема САУ

1) статическая ошибка астатической системы рана 0

2)

Для справки))

На основании принципа суперпозиции с помощью передаточных функций замкнутой системы определим изображение сигнала рассогласования называемое в технической литературе сигналом ошибки:

где E_x(p) – рассогласование по каналу управления,

E_f(p) – рассогласование по каналу возмущения,

W_x(p) – передаточная функция ошибки по каналу управления,

W_f(p) – передаточная функция ошибки по каналу возмущения.

Для оценки точности работы системы при единичных ступенчатых входном воздействии и возмущении определяется статическая ошибка, которая может быть получена из последнего выражения с помощью теоремы о конечном значении функции:

Передаточный коэффициент системы по каналу задания в установившемся режиме:

Установившаяся приведенная ошибка по каналу задания в статической системе при единичном ступенчатом воздействии:

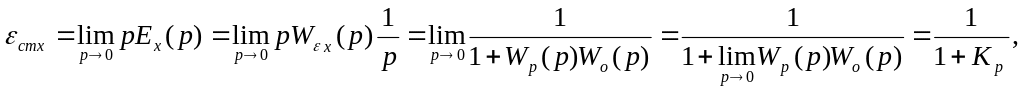в астатической системе 1-го порядка при [x(t)=t] :

в астатической системе 2-го порядка при [x(t)=0,5t²] :

19.

В лаборатории для испытаний аппаратуры при различных температурных режимах установлена система автоматического регулирования температуры. На линии подачи пара в нагреватель установлен регулируемый вентиль, управляемый напряжением u(t) – вход объекта. Для измерения температуры в лаборатории установлен термистор, подключенный к измерительной схеме. Полоса пропускания объекта (помещения лаборатории) ω_В=0,1с^-1 (или f_В= =ω_В/(2π)=0,016Гц), следовательно, температура в лаборатории будет изменяться очень медленно (с постоянной времени 10 с). Полоса пропускания термистора намного больше, чем полоса пропускания помещения лаборатории. В системе используется пропорционально-интегральный регулятор с коэффициентами k_П=5 и k_И=3.

Структурная схема системы имеет вид

.

На структурной схеме F(p) моделирует открытие двери в комнату: когда дверь открывается, то это идентифицируется с единичным ступенчатым воздействием, если дверь закрыта, то F(p)=0.

Каким должно быть входное воздействие (в вольтах), чтобы температура в комнате в установившемся режиме при закрытой двери была 25^оC ?

Насколько понизится температура в комнате (в установившемся режиме), если открыть дверь ?

Оцените устойчивость системы.

РЕШЕНИЕ:

Эта система астатическая по каналу возмущения и каналу управления, так как нулевой полюс находится в регуляторе, значит и по каналу управления и по каналу возмущения величина ошибки будет = 0 – выходная реакция. А статическая ошибка по каналу управления = 0.

На устойчивость влияет большая постоянная времени, параметры Пи-регулятора.

Тут получается разомкнутая система второго порядка, значит она всегда устойчива.

20.

По передаточной функции звена W(p)=10/(4p²+2p+1) рассчитайте величину коэффициента преобразования A(ω_i) и фазового сдвига θ(ω_i) на частоте ω_i=0,5 с^-1, качественно изобразите характеристики:

1. Амплитудно-частотную A(ω);

2. Фазо-частотную θ(ω);

3. Амплитудно-фазовую W(jω);

4. Переходную характеристику h(t).

РЕШЕНИЕ:

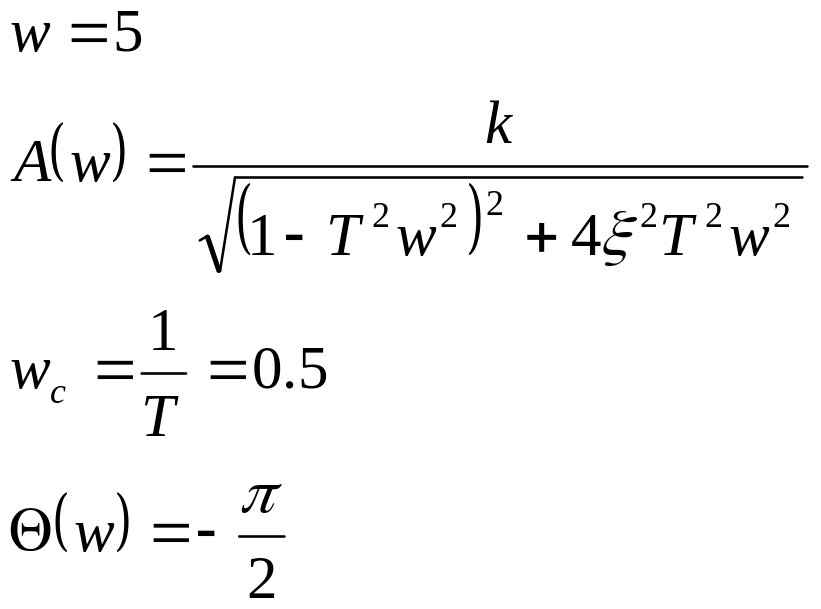
Сдвиг по фазе -90 градусов

Срисовать можно из паспорта типовых динамических звеньев САУ (колебательное звено)

Задача №21

Постройте ЛЧХ и рассчитайте критическое (соответствующее границе устойчивости) запаздывание _кр в САУ, где W(p)=e^-p и W₁(p)=k/p, k=2

Структурная схема САУ

Решение:

L,дБ Q,град

w=k=2

w,c^-1

Q₂(w)

L,дБ Q,град

L,дБ Q,град

Q(w)

При

Задача №22

Передаточная функция одноосного гиростабилизатора при коэффициенте демпфирования =0 в разомкнутом состоянии имеет вид ,

где k=40 с^-1, Т_г=6,510^-8 с.

Для демпфирования системы последовательно в цепь управления

введено корректирующее звено с передаточной функцией

.

Определите величину постоянной времени Т по критерию устойчивости Найквиста для ЛЧХ, при которой гиростабилизатор будет устойчив.

Решение:

На рисунке приведена асимптотическая ЛАХ и ЛФХ нескорректированной системы (сплошная линия)

Для устойчивости системы необходимо, чтобы ЛФХ пересекала линию в диапазоне частот . Поэтому постоянную времени корректирующего звена необходимо выбирать из условия

Система устойчива, например, при T=0,01с