Задача №1

Передаточная функция одноосного гиростабилизатора имеет вид

,

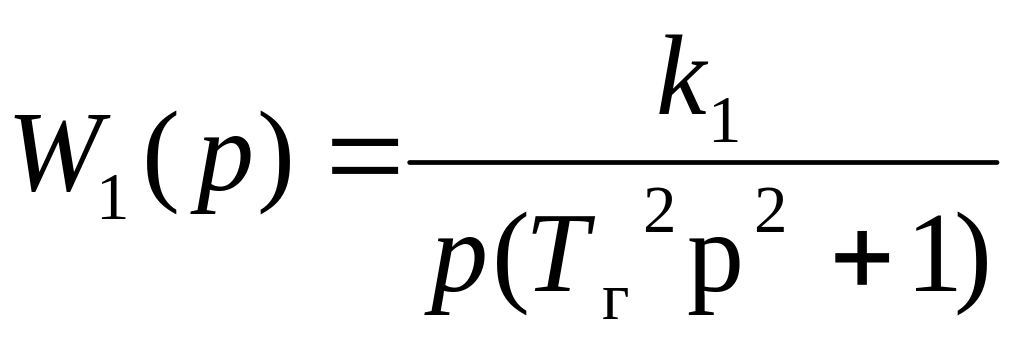где k₁=25с-1 – коэффициент усиления разомкнутой системы,

Тг=0,01с – постоянная времени.

Для демпфирования системы последовательно в канал управления

введено звено с бесконечной полосой пропускания (см.рис.) и

коэффициентом усиления k₂ = 1. Определите постоянную времени

корректирующего звена Т из условия устойчивости по критерию

Гурвица.

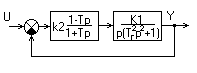
Структурная схема гиростабилизатора

Решение:

Передаточная функция разомкнутой системы , где -общий коэффициент усиления разомкнутой системы.

Характеристический полином замкнутой системы равен сумме полиномов знаменателя и числителя передаточной функции разомкнутой системы:

Используя критерий устойчивости Гурвица для автоматических систем, имеющих характеристический полином четвертого порядка, получаем условие устойчивости гиростабилизатора

Гиростабилизатор устойчив, например, при Т=0,015 с.

Задача №2

Постройте ЛЧХ и рассчитайте критическое (соответствующее границе устойчивости) запаздывание _кр в САУ, где W(p)=e^-p и W₁(p)=k/p, k=2

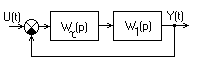
Структурная схема САУ

Р

Система неустойчива,согласно критерию Найквиста.

Фазовую характеристику дополняем до 0.

ешение: Передаточная функция разомкнутой системы , ,где

Задача №3

Передаточная функция одноосного гиростабилизатора при коэффициенте демпфирования =0 в разомкнутом состоянии имеет вид ,

где k=40 с^-1, Тг=6,510^-8 с.

Для демпфирования системы последовательно в цепь управления

введено корректирующее звено с передаточной функцией

.

Определите величину постоянной времени Т по критерию Найквиста для ЛЧХ, при которой гиростабилизатор будет устойчив.

Решение: На рис приведены асимптотическая л. а. х. и л. ф. х. нескорректированной системы (сплошная линия).

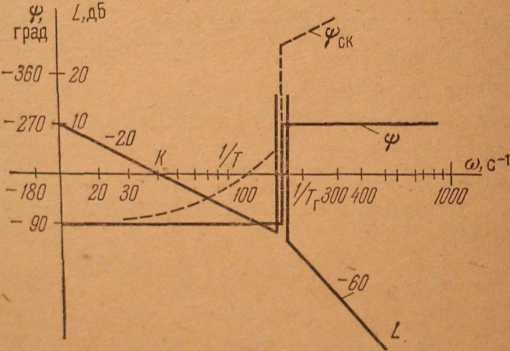
Для устойчивости системы необходимо, чтобы л. ф. х. пересекала линию в диапазоне частот . Поэтому постоянную вре­мени корректирующего звена необходимо выбирать из условия

Система устойчива, например, при Т = 0,01 с.

Задача №4

Передаточная функция разомкнутой системы имеет вид

,

где k=50с^-2 – общий коэффициент усиления разомкнутой системы,

T₁=1c, T₂=0,05c - постоянные времени.

Определите устойчивость замкнутой системы.

Решение: Для построения АФХ разомкнутой системы определим амплитудную частотную характеристику A(w) и фазовую частотную характеристику .

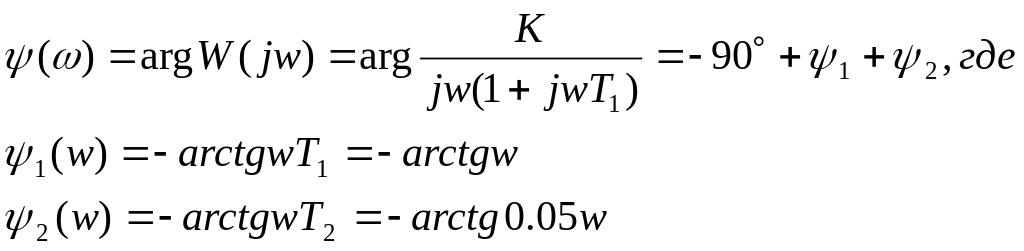
Вычислим A(w),ψ1(w), ψ2(w), ψ(w) для ряда значений w. Результаты вычислений сведем в таблицу:

	0	5	10	15	25	50	100
А	∞	18	6,9	3,56	1,32	0,28	0,045
	0	-26	-45	-56	-68	-79	-84
	0	-6	-11	-17	-26	-45	-64
	-90	-122	-144	-153	-184	-214	-238

По данным системы построена АФХ разомкнутой системы(рис).

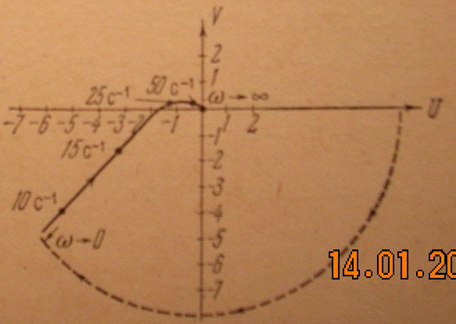
Знаменатель передаточной функции разомкнутой системы имеет один нулевой корень. Поэтому ветвь АФХ, соответствующую частотам дополним дугой окружности бесконечно большого радиуса так,чтобы вектор W(jw) повернулся по часовой стрелке на угол, равный 90 град(рис). Из рис видно, что АФХ разомкнутой системы охватывает точку(-1,0). Следовательно, замкнутая система неустойчива.