Экзаменационный билет № 16

1. Форсирующее звено. Звено чистого запаздывания.

2. Методика построения логарифмической частотной характеристики САУ: параллельное соединение звеньев.

1. Форсирующее звено.

, град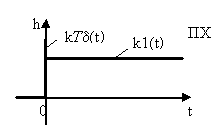

Дифференциальное уравнение переходная функция передаточная функция

ЛЧХ

L ()

+20

+90

20lgk

, с^-1

L, дБ

()

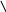
+45

с=1/T

Пример: ПД-регулятор.

Звено чистого (транспортного) запаздывания.

 - скорость перемещения ленты;

Q₁ – объем сыпучего продукта в единицу времени ,подается через шибер;

Q₂ – выход продукта.

Время чистого запаздывания .

В природе нет ни одного процесса без чистого запаздывания.

преобразуем по Лапласу это выражение (теорема запаздывания), получим отсюда

Ряд Паде

Аппроксимация, соответствующая n=2 при применении функции pade, Т=1с:

Рассмотренные выше наиболее часто встречающиеся на практике основные типы звеньев характеризуются отсутствием корней с положительной вещественной частью уравнений числителя (т.е. нулей передаточных функций) и знаменателя (т.е. полюсов) называются МИНИМАЛЬНО-ФАЗОВЫМИ. Из всех возможных звеньев с одинаковыми амплитудными характеристиками минимально-фазовые звенья обладают наименьшими по абсолютным значениям фазовыми характеристиками; второе их важное свойство – однозначное соответствие амплитудной и фазовой частотных характеристик (т.е. по амплитудной характеристике можно определить фазовую и наоборот.

- неминимально-фазовое звено.

2. Методика построения логарифмической частотной характеристики сау: параллельное соединение звеньев.

Статические системы.

Пусть передаточная функция разомкнутой статической САУ, состоящей из минимально-фазовых звеньев 1 порядка, имеет вид в реальных системах n(m-n).

Отобразим W(р) в область преобразований Фурье преобразуем математическое описание каждого элементарного звена к форме и расположим в порядке убывания величины Т_i:

Тогда

+90

+45

-45

-90

-180

, град.

L, дБ

lg, дек

, рад/с

-20

-20

0

-40

L()

L₂

()

₂

₃

1/T_n+1

1/T_n+2

1/T₁

L₄

L₅

1/T₂

L₃

_m+2

₅

₄

L₁()=20lgk

Алгоритм построения ЛАЧХ

1. На оси  нанесите точки _i=1/T_i. Проведите через эти точки вертикальные штриховые линии.

2. Проведите контурную линию с ординатой 20lgk слева до первой вертикальной линии.

3. До следующей вертикальной линии проведите контурную линию с наклоном -20 дБ/дек( – количество элементарных звеньев с одинаковыми Ti), если звенья апериодические, или +20 дБ/дек для дифференцирующих звеньев первого порядка.

4. Уменьшите (увеличьте) наклон на -20 дБ/дек (+20 дБ/дек) на следующей вертикальной линии до полного построения L().

Примечания

1. Для построения ЛАЧХ звена второго порядка используются приведенные характеристики в технической литературе или строятся по точкам вблизи _i=1/T_i, вдали с асимптотами  левой 0 дБ/дек , правой -40 дБ/дек для колебательного звена и +40 дБ/дек для звена дифференцирующего второго порядка.

2. Правило построения ЛЧХ систем с неминимально-фазовыми звеньями остаётся тем же.

3. ЛФЧХ строятся с использованием шаблонов или по точкам, рассчитанным аналитически.

Астатические системы.

Построение ЛАЧХ астатических систем 1-го порядка начинается с определения базовой частоты _б=k, где k - общий коэффициент усиления разомкнутой цепи регулирования и построения вспомогательной прямой с наклоном -20 дБ/дек влево от _i затем слева до первой штриховой вертикальной линии, построенной по пункту 1 алгоритма, по этой прямой проводится контурная линия и далее по правилу построения, кроме пункта 2 .

Построение ЛАЧХ астатических систем 2-го порядка отличается от построения ЛАЧХ астатических систем 1-го порядка значением частоты и наклоном вспомогательной линии -40 дБ/дек, в остальном методика построения совпадает.

ЛЧХ контура с отрицательной обратной связью.

Аналитический метод построения ЛЧХ контура с единичной ООС.

отсюда

Построение ЛЧХ контура по номограммам замыкания (Никольса).

Пусть амплитудно-фазовая частотная функция замкнутой системы имеет вид

(1) причем ,

Амплитудную и фазовую частотные функции замкнутой системы А_з() и _з() можно выразить через А() и разомкнутой цепи.

Согласно формуле (1) имеем

или, взяв обратные величины слева и справа, получим новое равенство

Подставим сюда и приравняем затем отдельно вещественные и мнимые части. Получим два равенства

Сложив сначала квадраты этих выражений, а затем поделив одно из них на другое, получим искомый результат

L(₁)

L₃(₁)

₃(₁)

0

Чтобы не иметь дело на практике с этими формулами, составлены НОМОГРАММЫ ЗАМЫКАНИЯ.

Отложив на осях абсцисс и ординат заданные значения (₁) и L(₁), находим значения 20lgА_з(₁) и (₁) на поле номограммы в точке с этими координатами. Таким образом по точкам строится вся частотная характеристика замкнутой системы.

Если контур с неединичной ООС, то его следует преобразовать к контуру с единичной ООС.

где W_А(j)=W_ПК(j)W_ОС(j). Тогда ЛЧХ замкнутой системы строится в два приёма

вначале строятся ЛЧХ контура с единичной ООС, затем строятся ЛЧХ функции и, наконец, результирующие ЛЧХ системы и

Экзаменационный билет № 17

1. Передаточная функция САУ.

2. Анализ качества САУ в динамике.