III. Контрольные задания и образцы решения

3.1 Задача 1

Имеется денежных единиц в рублях и денежных единиц в валюте, где − последняя цифра зачётной книжки, − предпоследняя цифра.

Рассматриваются три варианта:

1. Денежные средства в рублях размещаются в виде рублевого депозита, на который начисляются простые проценты по ставке .

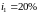2. Денежные средства в рублях размещаются в виде рублевого депозита, на который ежемесячно начисляются сложные проценты по номинальной ставке .

3. Валютные средства размещаются в виде валютного депозита, на который ежеквартально начисляются сложные проценты по номинальной ставке .

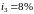Сроки операции: 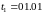(1 января) − дата открытия депозита, 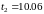(10 июня) − дата закрытия депозита (год не високосный).

Возможно конвертировать рубли в валюту, а валюту в рубли. В начале операции единица валюты продается по цене 31 рубль, а покупается по цене 30 рублей. В конце операции ожидается, что единица валюты будет продаваться по цене 32 рубля, а покупаться по цене 31 рубль 50 копеек.

Выполните следующие расчёты, рассматривая варианты с конвертацией и без конвертации. Конечные результаты запишите в рублях.

1. Определите начисляемые проценты и наращенные суммы. При вычислении простых процентов используйте британский, французский, германский методы. При вычислении сложных ежемесячных процентов используйте смешанный метод и формулу с дробным числом периодов начислений. При вычислении сложных ежеквартальных процентов используйте метод, при котором проценты на последний период не начисляются, если он меньше целого периода начисления.

2. Для всех полученных наращенных сумм вычислите простые учётные ставки.

3. Оцените реальные суммы наращения при неизменном среднемесячном темпе инфляции .

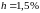Результаты, полученные в пунктах 1-3, занесите в таблицу 1 (см. след. страницу). Суммы в валюте переведите в суммы в рублях по курсу обмена в конце операции.

4. Определите, какой вариант, с конвертацией или без конвертации, наиболее выгоден. В каком случае полученные проценты компенсируют инфляционные потери?

Таблица 1. Результаты расчетов первого задания

Процентные ставки

Метод вычислений

Проценты

Наращенные суммы

Учётные ставки

Реальные суммы

Досрочные суммы

Вся сумма в рублях

британский

французский

германский

смешанный

дробный

Вся сумма в валюте

без % за посл. период

Без конвертации

Рубли

британский

французский

германский

смешанный

дробный

Валюта

без % за посл. период

Всего вместе в лучшем случае

при каком методе?

5. Для рублевых депозитов вычислите суммы, получаемые за время 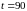дней до срока погашения 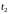, совмещая начисление процентов по ставке наращения и дисконтирования по учётной ставке. Результаты добавьте в таблицу 1.

6. Вычислите эффективную ставку, соответствующую ставке .

7. Вычислите простую ставку, эквивалентную ставке и сложную

ставку (проценты начисляются 12 раз в год) эквивалентную ставке .

8. Определите сложную процентную ставку с начислением 2 раза в год

эквивалентную ставке .

9. Используя математический учёт (дисконтирование), определите

певоначальную сумму для ставок , , 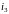, если в конечном результате необходимо получить сумму рублей.

10. Для первоначальной сумм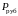ы и конечной суммы

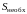
определите срок депозита для всех ставок , , .

Образец решения пр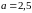и и .

Имеется 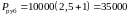рублей и единиц валюты.

В начале операции курсы прямого и обратного обмена валюты в рублях равны соответственно:

, .

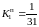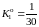Так как в конце операции нас интересуют только суммы в рублях, нам важен только курс обратного обмена, который равен:

.

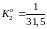Вариант конвертации в рубли. Если все суммы конвертировать в рубли, то получим:

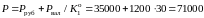рублей.

Вариант конвертации в валюту. Если все суммы конвертировать в валюту, то получим:

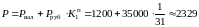ед. валюты.

1. Исследуем различные варианты начисления процентов с конвертацией и без конвертации.

Рассмотрим вариант с конвертацией всей суммы в рубли. Вычислим наращенные суммы и начисляемые простые проценты на сумму 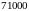рублей двумя методами.

I. Рассмотрим три варианта размещения средств на рублёвый депозит под простой процент.

Подсчитаем точное число дней длительности депозита: 31 день января, 28 дней февраля, 31 день марта, 30 дней апреля, 31 день мая, 10 дней июня, всего получаем 160 дней, учитывая, что день открытия и закрытия депозита считается за один день. Подсчитаем приближённое число дней длительности депозита (для германской практики начисления процентов): 30 дней пяти месяцев, 10 дней июня, всего получаем 159 дней, учитывая, что день открытия и закрытия депозита считается за один день.

Британский метод (число дней в году и в периоде начисления равно точному календарному числу дней):

,

.

Французский метод (число дней в году равно 360, число дней в периоде начисления равно точному календарному числу дней):

,

.

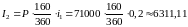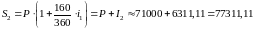Германский метод (каждый полный месяц равен 30 дням, число дней в году равно 360):

,

.

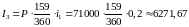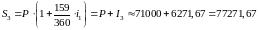II. Вычислим наращенные суммы и начисляемые сложные проценты на сумму 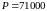рублей смешанным методом и методом с дробным числом периодов.

Смешанный метод. Обозначим через 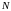целое число периодов начисления, а через оставшуюся дробную часть. Тогда 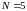это количество полных месяцев, а – это оставшиеся 10 дней июня: , 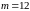– количество месяцев в году. Таким образом, получаем

,

.

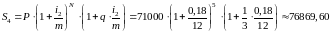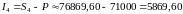Метод с дробным числом периодов начисления. Обозначим через длительность депозита в днях ( ), через длительность месяца (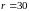 ).Тогда

,

.

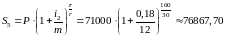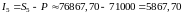Рассмотрим вариант с конвертацией всей суммы в валюту. Вычислим наращенные суммы и начисляемые простые проценты на сумму единиц валюты.

III. Вычислим наращенную сумму и проценты, начисляемые ежеквартально без начисления процентов на период меньше квартала. В этом случае количество полных кварталов 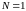, количество кварталов в годе .

Конвертируем полученную величину в рубли:

,

.

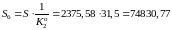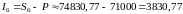Рассмотрим вариант без конвертации.

Вычислим аналогично I и II наращенные суммы и проценты с имеющихся 35000 рублей и аналогично III наращенную сумму и проценты с 1200 единиц валюты.

Британский метод:

,

.

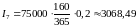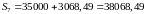Французский метод:

,

.

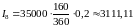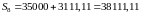Германский метод:

,

.

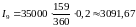Смешанный метод.

,

.

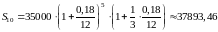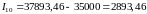Метод с дробным числом периодов начисления.

,

.

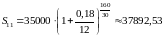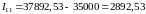Наращение суммы в валюте.

.

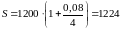Конвертируем полученную величину в рубли:

,

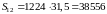Процент определяем относительно суммы в рублях по первоначальному курсу покупки:

.

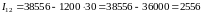Определим суммарный вариант как лучший из всех возможных схем в рублях и приведенной в рубли суммы в валюте. Наибольшее наращение в рублях получено по французской схеме. Тогда:

.

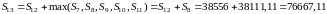
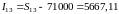Полученные результаты запишем в таблицу 1.

2. Возьмём 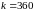(базовый период), (длительность депозита). Простые учётные ставки будем вычислять по формуле:

, .

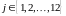Например

, .

Полученные результаты запишем в таблицу 1.

3. Реальные суммы наращения с учётом темпа инфляции вычислим по формуле:

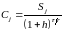
Например

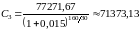
Полученные результаты запишем в таблицу 1.

4. Как видно из таблицы, при описанных условиях выгодно конвертировать валюту в рубли и общую сумму разместить под простой процент. Наибольшее наращение достигается при французском методе начисления процентов.

При конвертации в рубли реальные суммы наращения не ниже начальных, то есть компенсируют инфляционные потери. Во всех остальных случаях инфляционные потери больше полученных процентов.

5. Для рублёвого депозита суммы, учтённые за время 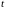, вычисляются по формуле:

, .

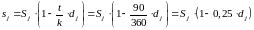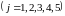Например

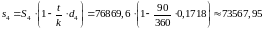
Полученные результаты добавим в таблицу 1.

Таблица 1. Результаты расчетов первого задания

	Процентные ставки		Метод вычислений		Проценты		Наращенные суммы		Учётные ставки		Реальные суммы		Досрочные суммы
Вся сумма в рублях			британский		6224,66		77224,66		18,14%		71329,71		73723,29
			французский		6311,11		77311,11		18,37%		71409,56		73761,11
			германский		6271,67		77271,67		18,26%		71373,13		73743,85
			смешанный		5869,60		76869,60		17,18%		71001,75		73567,95
			дробный		5867,70		76867,70		17,18%		71000,00		73567,12
Вся сумма в валюте			без % за посл. период		3830,77		74830,77		11,52%		69118,56
Без конвертации	Рубли			британский		3068,49		38068,49		18,14%		35162.53
				французский		3111,11		38111,11		18,37%		35201.90
				германский		3091,67		38091,67		18,26%		35183.94
				смешанный		2893,46		37893,46		17,18%		35000.86
				дробный		2892,53		37892,53		17,18%		35000.00
	Валюта			без % за посл, период		2556,00		38556,00		14,92%		35612.82
	Всего вместе в лучшем случае		при французском методе		5667,11		76667,11		16,63%		70814,72

6. Вычислим эффективную ставку, соответствующую ставке .

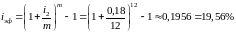
7. Вычислим простую ставку, эквивалентную ставке :

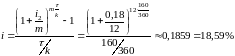
и сложную ставку (проценты начисляются 12 раз в год) эквивалентную ставке :

.

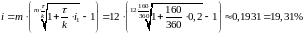8. Определим сложную процентную ставку с начислением раза в год эквивалентную ставке .

.

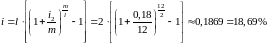9. 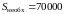. Первоначальную сумму в случае начисления простых процентов в течение года определим следующим образом:

.

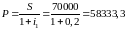Вычислим первоначальную сумму при ежемесячном начислении в течение года сложных процентов с годовой ставкой .

.

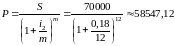Для использования валютного депозита учтём двойную конвертацию. Напомним, что при ежеквартальном начислении .

.

10. Вычислим сроки депозитов для ставок , , :

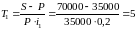лет,

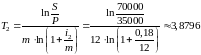года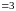 года 321 день,

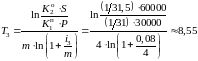года=8 лет 201 день.