Федеральное агентство по образованию

Красноярская государственная архитектурно-строительная академия

Моделирование строительного производства.

Сетевые модели

Методические указания к практическим занятиям

по дисциплине "Организация строительного производства"

для студентов специальности 290300 "Промышленное и

гражданское строительство"

Красноярск, 2005

УДК 69.05

ББК 38.6

Моделирование строительного производства. Сетевые модели: методические указания к практическим занятиям по дисциплине ''Организация строительного производства'' для студентов специальности 290300 "Промышленное и гражданское строительство". Красноярск. КрасГАСА, 2005. 36 с.

Составители:

И. И. Терехова

Л. Н. Панасенко

Печатается по решению редакционно-издательского совета академии

©Красноярская государственная архитектурно-строительная академия, 2005

3

Введение

Строительное производство представляет собой сложную организационно-технологическую систему, которую для удобства изучения можно представить в виде графической модели.

Под организационно-технологической моделью возведения объектов следует понимать перечень строительно-монтажных работ, порядок их выполнения и взаимосвязь между работами в соответствии с выбранной технологией и организацией производства, нормами и правилами, а также условиями рационального использования ресурсов.

Моделированием называется процесс обоснования, выбора, разработки моделей и исследования их поведения в различных условиях.

4

1. Модели, применяемые в организации строительства

Известны различные виды организационно-технологических моделей строительства объектов, и в ряде случаев можно установить наиболее рациональные области применения каждой из них.

В качестве организационно-технологических моделей строительного производства применяются:

• линейные графики (графики Т.Л. Ганта);

• циклограммы М.С. Будникова;

• матрицы (таблицы);

• сетевые графики.

Линейный график очень прост в исполнении и наглядно отображает однозначную взаимосвязь и последовательность работ во времени. Однако здесь динамическая система строительства представлена статической схемой, которая в лучшем случае может отобразить положение на объекте, сложившееся в какой-то определённый момент времени. Линейный график не может отобразить сложность моделируемого в нём процесса.

Отсюда основные недостатки линейных графиков:

-отсутствие наглядно обозначенных взаимодействий между работами; зависимость выявляется составителем только один раз в процессе разработки графика и фиксируется как неизменная; в результате график теряет своё практическое значение вскоре после начала реализации проекта, что ограничивает возможность его использования в ходе строительства объекта;

-негибкость, жёсткость структуры линейного графика, что приводит к сложности его корректировки при изменении условий, требуется его многократное пересоставление;

-сложность вариантной переработки и ограниченная возможность прогнозирования хода работ;

5

-сложность применения современных математических методов и вычислительной техники для механизации расчётов параметров графиков.

Все перечисленные недостатки снижают эффективность планирования, организации строительного производства и управления им при использовании линейных графиков.

Несмотря на обозначенные выше недостатки, линейные календарные графики не потеряли своего значения и в настоящее время. В современных условиях развития индивидуального строительства малоэтажных домов (коттеджей) применение линейных графиков не только возможно, но и целесообразно. Линейные графики также находят применение в моделировании отдельных процессов, например, при разработке технологических карт и карт трудовых процессов.

Календарный линейный график строится в системе координат: ось абсцисс - время, ось ординат - наименование работ. Для каждой работы выделена горизонтальная полоса, в которой размещается линия, равная по длине продолжительности работы. При поточной организации строительства работа на равных захватках показывается смещением отрезков относительно друг друга. Принципиальная схема линейного графика изображена на рис. 1.1.

Линейные циклограммы являются модификацией линейных графиков, отображающей поточный график выполнения работ. В практику строительства линейные циклограммы вошли в начале 60-х годов прошлого века.

Как и линейные графики, циклограммы строят на плоскости в двухмерной системе координат: "работа - время". По оси абсцисс откладывают рабочее время, а по оси ординат - объекты строительства или их части (захватки), на которых должны выполняться работы. Работа изображается наклонной линией, которая показывает движение каждой бригады по фронту работ одной захватки и переход бригады на другую захватку. Продолжительность работ определяется проекцией линии на ось абсцисс.

6

Таблица 1.1

Жилой дом.

Секция 1

Секция 2

Секция 3

Секция 4

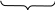
1-я захватка 2-я захватка 3-я захватка 4-я захватка

№ п/п	Наименование работ	Продолжительность, дни
		1-я захватка	2-я захватка	3-я захватка	4-я захватка
1	Устройство подготовки под полы	2	2	2	2
2	Штукатурные работы	4	4	4	4
3	Малярные работы	3	3	3	3
4	Устройство чистых полов	2	2	2	2

№ п/п	Наименование работ	Продолжительность работ на захватке, дни	Календарные дни Апрель 2003 май
			1	2	3	4	7	8	9	10	11	14	15	16	17	18	21	22	23	24	25	28	29	30	1
			Рабочие дни
			1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23
1	Устройство подготовки под полы	2
2	Штукатур-ные работы	4
3	Малярные работы	3
4	Устройство чистого пола	2

Рис.1.1. Линейный календарный график

7

На рис.1.2. приведён пример построения циклограммы разноритмичного потока. Работы выполняются четырьмя специализированными бригадами, действующими на четырёх захватках.

№ п/п	Место работ	Календарные дни Апрель 2003 май
		1	2	3	4	7	8	9	10	11	14	15	16	17	18	21	22	23	24	25	28	29	30	1
		Рабочие дни
		1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23
1	4-я захватка
2	3-я захватка
3	2-я захватка
4	1-я захватка

Рис.1.2. Циклограмма

Построение циклограммы основано на применении технологических нормалей, каждая из которых разработана для одной типовой захватки и описывает одновариантную последовательность выполнения работ.

Циклограммы нашли широкое применение при внедрении и изучении поточного строительства. Однако, поскольку циклограммы, как отмечалось выше, представляют собой модификацию линейных графиков, им также присуще большинство их недостатков.

Матричные модели (математическое описание строительного процесса) представляют строительное производство в виде математической матрицы, на которой могут быть вычислены все параметры календарного плана без его графического изображения. С помощью матричной модели можно представить всё многообразие строительных потоков и вычислить необходимые параметры. Расчёт параметров потока можно представить в виде клеточной матрицы, строки которой соответствуют, например, захваткам, а столбцы - работам, внутри клеток

8

временные параметры их выполнения. Расчёт параметров потока ведётся по специально разработанному алгоритму. Пример расчёта строительного потока математическим способом изображён на рис.1.3.

Число захва-ток	Номер бригады (работы)				∑Kj	∑tпер.j	∑Kj+ ∑tпер.j
	1	2	3	4
1	0 2 2	2 4 6	9 3 12	15 2 17	11	6	17
2	2 2 4	6 4 10	12 3 15	17 2 19	11	6	17
3	4 2 6	10 4 14	15 3 18	19 2 21	11	6	17
4	6 2 8	14 4 18	18 3 21	21 2 23	11	6	17
∑Кi	8	16	12	8	44	24	68

Рис.1.3.Матрица

Последовательность расчета матрицы:

1. Находим продолжительность работы бригады (К_j), для чего суммируем продолжительность работ бригады на всех захватках.

2. Определяем начало и окончание работ на захватках. В верхний левый угол первой клетки заносим начало работы первой бригады на 1-й захватке (обычно 0), а в нижний правый угол – окончание работы первой бригады на первой захватке, которое равно сумме начала и ее продолжительности. Время окончания работы первой бригады на 1-й захватке считается началом ее работы на 2-й захватке, поэтому без изменения переносим его в левый верхний угол второй клетки

9

этого же столбца, затем определяем окончание работы первой бригады на 2-й захватке, как делали ранее, и т.д.

Таким образом, определяем начала и окончания работ первой бригады на всех захватках.

Дальнейший расчет по столбцам ведут в зависимости от общей продолжительности работ бригад. Если продолжительность работы следующей бригады больше продолжительности работы предыдущей, то расчет ведут сверху вниз, а если меньше, то снизу вверх.

Из рис.1.3 следует, что общая продолжительность работ второй бригады больше продолжительности работ первой бригады(168), поэтому расчет начал и окончаний работ второй бригады на захватках начинаем сверху, т.е. с момента готовности фронта работ на 1-й захватке.

Из нижнего угла первой клетки первого столбца время окончания работ на 1-й захватке переносим в левый верхний угол первой клетки второго столбца, что соответствует началу работ второй бригады. Далее расчет ведем соответственно уже рассмотренному примеру.

Продолжительность работы третьей бригады меньше продолжительности работы второй бригады (1216),поэтому расчет начал и окончаний работ третьей бригады ведем снизу вверх. В левый угол последней клетки третьего столбца переносим время окончания работ второй бригады на последней захватке, это же время соответствует окончанию работы третьей бригады на предыдущей захватке. Начало работы бригады на 3-й захватке определяем как разность между окончанием работы и ее продолжительностью. Аналогично рассчитываем всю матрицу. Величина нижнего угла последней клетки матрицы равна общей продолжительности работ.

Значения организационных перерывов между работами бригад на захватках равно разности значений цифр в накрест лежащих углах клеток матрицы для

10

каждой пары смежных потоков. Суммарное значение организационных перерывов заносят в последнюю строку матрицы.

Одним из достоинств использования матриц для расчета потоков является получение более полного набора временных параметров потока. Кроме временных параметров, матричный метод дополнительно дает общую продолжительность потока, суммарную продолжительность всех работ на отдельно взятой захватке (объекте), продолжительность работы любой бригады на всех захватках (объектах), продолжительность всех организационных и технологических перерывов, простой бригад на фронтах работ, уровень совмещения работ, который определяется по формуле

С= ΣК_j ∕ (ΣК_j+Σt_пер.j),

где С - степень совмещения работ, т.е. степень использования фронта работ бригадами; К_j- суммарное значение продолжительностей работы всех бригад на захватках, дни; t_пер.j-суммарное значение продолжительностей организационных перерывов между работами бригад, дни.

В рассматриваемой матрице (рис. 1.3) коэффициент, характеризующий использование фронта работ бригадами (коэффициент плотности графика работ), C=0,65.

С= ΣК_j ∕ (ΣК_j+Σt_пер.j) = 44 ∕ (44+24) = 0,65.

Сетевые модели – наиболее эффективное средство планирования и организации производства. Они наглядно отражают технологическую последовательность выполнения работ и взаимосвязи между работами. Сетевые модели позволяют выделять работы, от которых зависит общая продолжительность возведения объекта (работы критического пути), что в процессе оперативного управления ходом строительства дает возможность

11

руководителям сосредоточить внимание на выполнении этих работ. При возникновении отклонения от запланированного хода работ руководители могут перераспределить ресурсы и прогнозировать дальнейший ход строительства (резервы времени). Для выполнения расчетов и решения оптимизационных задач сетевые модели позволяют использовать вычислительную технику.

Своим появлением и развитием сетевые модели обязаны теории ''графов''. Графом называют геометрическую фигуру, состоящую из конечного или бесконечного множества точек и соединяющих эти точки линий.

Первая попытка использовать сетевую модель для целей планирования хода работ и контроля относится к 1956 г., когда американская компания ''Дюпон'' образовала группу для разработки методов управления строительством. Этим коллективом был разработан метод ''критического пути''.

В СССР сетевые модели начали разрабатываться и изучаться в 1962 г.

Подготовка под полы

Iз IIз IIIз IVз

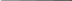
Штукатурные работы

Iз IIз IIIз IVз

Малярные работы

Iз IIз IIIз IVз

Устройство чистых полов

Iз IIз IIIз IVз

Рис. 1.4. Сетевая модель комплекса отделочных работ

12

Пример определения продолжительности цикла отделочных работ в 4 секционном жилом доме показан на рис. 1.1-1.4. Наименование и продолжительность работ на захватке приведены в исходных данных (табл. 1.1).