Оглавление

Структурная схема задачи оценивания 3

Типовая задача определения параметров движения ц.м. КА 3

Оценки и их свойства 4

Исторический аспект МНК (метода наименьших квадратов) 6

Сущность метода наименьших квадратов 6

Постановка линейной регрессионной задачи статистического оценивания и индикации динамических систем. 7

Геометрическая интерпретация критерия качества МНК 7

Алгоритмы линейного оценивания МНГ 8

1. Общий вид алгоритма 8

2. Точность МНК оценок 9

3. Статистические свойства МНК оценок. 9

Примеры оценивания по МНК( линейные случаи) 10

ПРИМЕР 1: простейшая задача регрессионного анализа 10

ПРИМЕР 2: Классическая задача линейного регрессионного анализа 10

МНК в нелинейных задачах оценивания 11

1. Постановка задачи: 11

2. Общий вид алгоритма оценивания 11

Условия окончания процесса последовательных приближений 11

Получение линеаризованной модели 12

Причины расхождения (не схождения) алгоритмов оценивания для получения оценок: 12

Точности МНК оценок для нелинейного случая 14

Метод наименьших модулей (МНМ). 14

Эффективность МНМ 15

Байесовский подход к учету априорной информации 15

Понятие априорной информации 15

Использование формулы Т. Байеса в задачах оценивания состояния динамических систем 16

Универсальный критерий байесовского оценивания. 16

Виды функции потерь 17

Метод максимального правдоподобия (ММП) 18

ММП в линейных задачах оценивания 18

Общая постановка задачи оценивания данных по ММП: 18

Алгоритм линейного оценивания ММП в предположении нормального (Гауссовского) распределения ошибок измерений 18

Функция правдоподобия 19

Алгоритм оценивания ММАВ 19

Пример оценивая с помощью ММАВ метода. 19

Свойства ММАВ оценок 20

Другие свойства ММАВ оценок 20

Теоритические основы динамической фильтрации сигналов(измерений). 21

Классификация случайных процессов 21

Понятие марковского процесса. 22

Примеры марковских процессов 22

1.Белый нормальный шум 22

2.Винеровский процесс 23

3.Математические модели стохастических динамических систем 23

Алгоритмы динамической фильтрации 23

История создания теории динамической фильтрации 23

Основные этапы развития теории динамической фильтрации 24

Фильтр Р. Калмана 24

Общая постановка задачи 24

Математическая постановка задачи 25

Структурная схема задачи оценивания

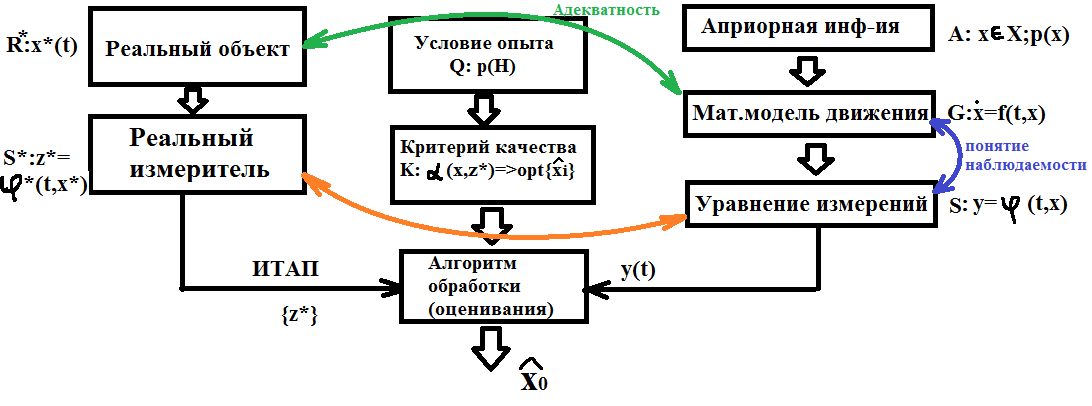
Рис 1.1 Схема

ИТНП – Измерения текущих навигационных параметров

_- плотность распределения вероятности

Типовая задача определения параметров движения ц.М. Ка

Подобная зада реализуется на практике в виде разработки и использования спец пакета программ (АКП, Н50), который предназначен для определения или уточнения параметров движения ц.м. по ИТНП.

Вычисление статических характеристик сеансов ИТНП относительно прогнозируемой траектории, расчетов и выдачи отклонений параметров траектории от прогнозируемой траектории.

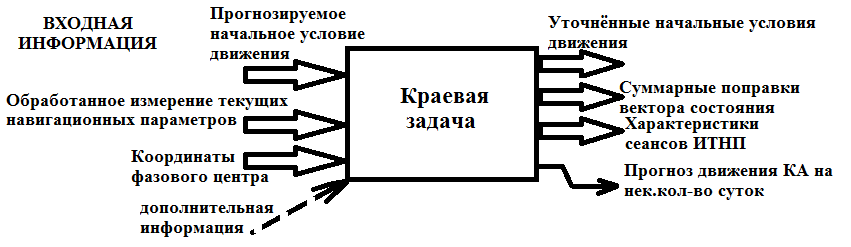
Рис1.2. Схема

Как правило при решение задач определения параметров движения на практике накладываются ограничения:

• На максимальное количество используемых ИТНП

• Максимальное количество измерений за сеанс

• Спектр возмущений, которые определяются используя ММД

• Состав оцениваемого вектора состояния

Оценки и их свойства

Оценкой называется численное значение функций результатов измерений, построенной в соответствии с некоторым методом их обработки.

Оценка также называется статистикой (т.е. функцией измерительной информации)

Оценка характеризуется :

• Состоятельность

• Несмещенность

• Эффективность

• И др..

Состоятельность

Оценка называется состоятельной если при неограниченном увеличении объекта выборки измерений она стремиться по вертикале к действительному значению оцениваемого параметра

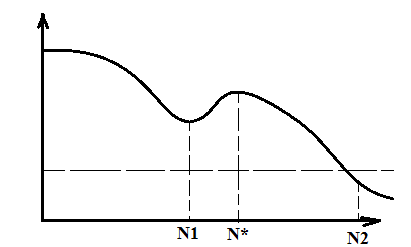
Рис 1.3

Несмещенность

Оценка называется несмещённой если математическое ожидание оценки совпадает с реальной величиной

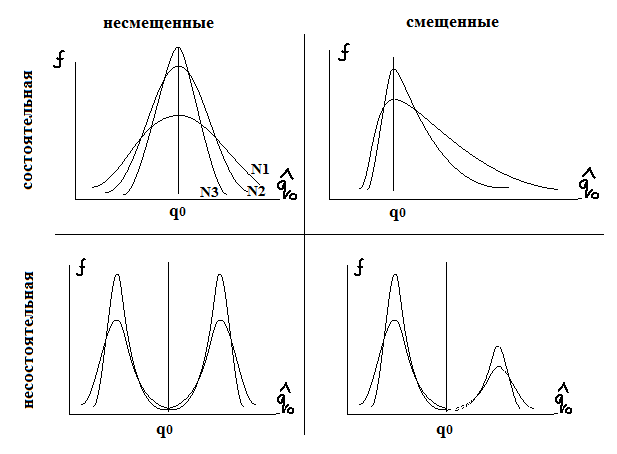
Рис.1.4

Эффективность

Говорит о том, что мы можем получить разные оценки разными методами. Метод дающий минимальную дисперсию среди других методов есть наиболее эффективный метод. А оценка, полученная таким методом есть эффективная оценка. Несмещённая оценка называется эффективной, если её дисперсия минимальна на множестве всех возможных методов статистической обработки данной выборки измерений

Асимптотическая эффективность

Пример

Рассмотри задачу оценки высоты полета ЛА, находящегося на круговой траектории по изменениям высоты полета в точках

Дано: Действительная высота полета

Определить

Решение

1) Пусть оценка ф-ся как САО

несмещена

2)

эффективная

3) неравенство Чербышева

- состоятельна

Исторический аспект мнк (метода наименьших квадратов)

Метод наименьших квадратов придуман Лежандром (1805г.) и Гауссом. (1795г. 1809г.)

В 1792 году Лаплас предложил метод наименьших модулей (МНМ).

В 1831 году Коши предложил минимаксный метод.

Сущность метода наименьших квадратов

Рис 2.1

невязка?

В векторном виде: , что соответствует

Часто исходя из того, что мы проводим измерения не одинаковыми (не равноточными средствами) приходят к : , где W-vfnhbwf dpdtibdfybz? Gjpdjkztn extcnm ythfdyjnjxyjcnm bpvthtybq

ОБРАБАТЫВАТЬ ИНФОРМАЦИЮ НАДО РАЗУМНО

МНК в линейных задачах оценивания

Постановка линейной регрессионной задачи статистического оценивания и индикации динамических систем.

Дано:

1. Математическая модель динамической системы , ; где – матрицант

2. Математическая модель измерительных средств

   1. План измерений Р: - вид измеряемого параметра

   2. Уравнение измерений S: ,

,

Где

Введем составной вектор измерений.

3. Условие опыта:

   1. Погрешности аддитивный

   2. Свойства ошибок измерений

А.1

А.2 ;

B.1 ;

B.2 ;

B.3 матрица колориации

3. Реальная выборка результатов измерений Z:

Z представляет собой конкретную реализацию случайного вектора

4. Априорная информация о А отсутствует

5. Критерий качества К :

– весовая матрица, которая учитывает неравноточность измерений

Требуется определить оптимальную оценку с выбранным критерием качества