1.Предмет нг.

НГ- это раздел геометрии , который

-Изучает теоретические основы методов построения проекций геометрических тел

-Решает позиционные и метрические задачи на проекциях этих тел.

2. Методы проецирования. Центральное пр-ние. Параллельное пр-ние, его основные свойства.

отображение геом.фигуры на плоскость\др. поверхность можно получить путем проецирования ее точек на эту плоскость.

Центральное пр-ние.

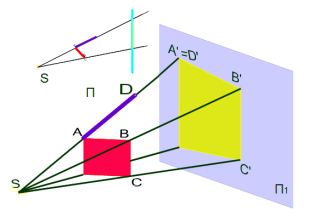
Ортогональное пр.

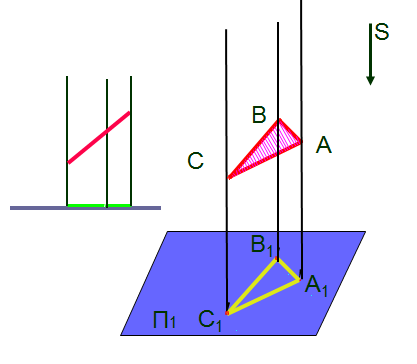
Параллельное пр-ние

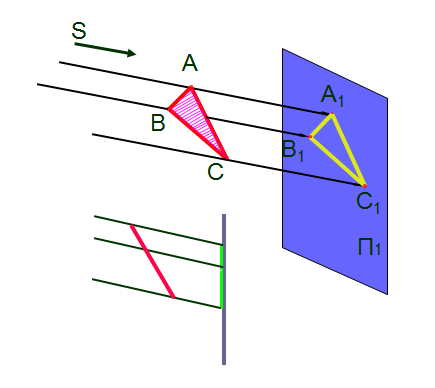
Св-ва орт. и паралл. проецирования 1)Проекция точки на плоскость есть точка (А )

2) Проекцией прямой в общем случае является прямая. Она вырождается в точку, если прямая параллельна направлению проецирования.

( )

3) Если точка принадлежит линии, то проекция точки принадлежит проекции линии

) 4) Точка пресечений линий проецируется в точку пересечения их проекций.

(a b=KÞ a₁ b₁= )

5) Проекции параллельных прямых – параллельны. (m II n Þ m₁II n₁ )

6) Если плоская геометрическая фигура параллельна плоскости проекций, то проекция этой фигуры равновелика самой фигуре. ФIIП ÞIФI=IФ₁I

7)проекция фигуры не изменяется при параллельном переносе плоскости проекции.

3. Прямая и обратная задачи начертательной геометрии, обратимость чертежа.

Прямая задача – создание плоского чертежа объекта

Обратная задача – возможность по плоскому чертежу восстановить пространственный вид объекта.

4.Комплексный чертеж точки. Осный и безосный способы построения комплексного чертежа.

безосный компл.чертеж точки.условия связи: -горизонт. и фронт. проекции точки принадлежат вертикальной линии связи.

-проф. и фронт. проекции точки принадлежат горизонтальной линии связи.

-горизонт. и проф. проекции точки принадлежат ломаной линии связи.

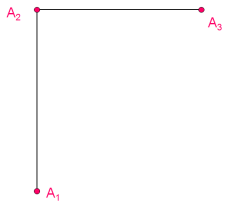
осный комплексный чертеж

5. Комплексные чертежи линий. Прямая общего положения. Линии уровня и проецирующие. Конкурирующие точки.

Аксиомы и теоремы, характеризующие свойства прямой линии:

- Аксиома. Через любые две различные точки проходит одна и только одна прямая.

-Теорема. Две различные прямые могут иметь не более одной общей точки.

положение прямых в пространстве.

-Прямые общего положения- не параллельны и не перпендикулярны ни одной плоскости проекций

-Прямые уровня – параллельны плоскостям проекций.

Горизонталь h - параллельна П₁

Фронталь f - параллельна П₂

Профильная прямая p - параллельна П₃

Проецирующие прямые- перпендикулярны плоскостям проекций :

Горизонтально-проецирующая – перпендикулярна П₁

Фронтально-проецирующая – перпендикулярна П₂

Профильно-проецирующая – перпендикулярна П₃

Комплексный чертеж ГОРИЗОНТ.

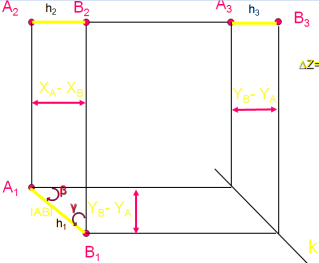
ФРОНТАЛИ

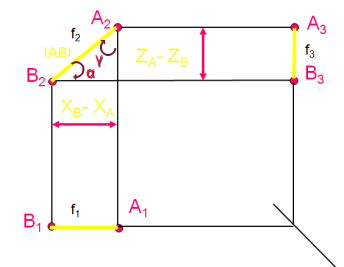
ПРОФ.

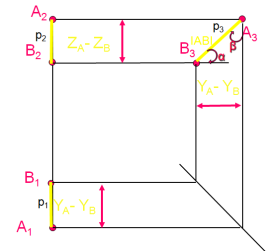
Прямая, перпендикулярная какой-либо плоскости- проецирующая.

Точки, принадлежащие одной и той же прямой- конкурирующие, относит. плоскости проекции, которой перпендикулярна прямая. Из двух конкурирующих точек видна та, которая расположена выше\ближе к вам.

6.Принадлежность точки прямой линии.

В зависимости от формы линии можно разделить на: прямые, ломаные, кривые.

Прямая есть такое множество точек, свойства которого определяются аксиомой прямой:

Через любые две различные точки проходит одна и только одна прямая;

и теоремой , которая следует из аксиомы прямой:

две различные прямые могут иметь не более одной общей точки.

7.Плоскости. Классификация плоскостей.

Аксиомы

-Через любые три точки не принадлежащие одной прямой проходит одна и только одна плоскость

Следствия

Через прямую и не принадлежащую ей точку проходит одна и только одна плоскость

Через две пересекающиеся прямые проходит одна и только одна плоскость

Через две различные параллельные прямые проходит одна и только одна плоскость

-Если две точки прямой принадлежат плоскости, то вся прямая принадлежит плоскости

-Две плоскости пересекаются по прямой

Положение плоскостей в пространстве:

-Плоскости общего положения- не параллельны и не перпендикулярны ни одной плоскости проекций

-Плоскости уровня – параллельны плоскостям проекций

Горизонтальная пл-ть уровня - параллельна П₁

Фронтальная пл-ть уровня - параллельна П₂

Профильная пл-ть уровня - параллельна П₃

Проецирующие плоскости- перпендикулярны плоскостям проекций Горизонтально-проецирующая– перпендикулярна П₁

Фронтально-проецирующая – перпендикулярна П₂

Профильно-проецирующая– перпендикулярна П₃