3.3.3. Логарифмически-нормальное распределение

Логарифмически-нормальное распределение применяют для описания процессов усталостного разрушения, износовых отказов, при исследовании событий, обусловленных совместным действием износа и старения материалов, для описания процессов восстановления и в ряде других случаев.

Плотность логарифмически-нормального распределения описывается формулой:

f(t) = ,

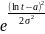где а – параметр распределения, определяемый по результатам испытаний.

Кривая логарифмически-нормального распределения аналогична кривой нормального распределения, но с несимметричной петлей (рис. 3.3 в).

3.3.4. Распределение Вейбулла

Распределение Вейбулла применяется в моделях со «слабым звеном», а также в сложных системах в случаях если система состоит из группы независимых элементов, отказ каждого из которых приводит к отказу всей системы. Наряду с логарифмически-нормальным распределением распределение Вейбулла хорошо описывает наработку деталей по усталостным разрушениям, наработку до отказа подшипников и др.

Распределение Вейбулла является достаточно универсальным, благодаря возможности варьирования двумя его параметрами: α – параметр формы и β – параметр масштаба.

Плотность распределения вероятностей (рис. 3.3 г):

f(t) = αβ .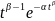

Установлены следующие закономерности возникновения отказов:

• внезапные отказы – экспоненциальному закону;

• постепенные отказы – подчиняются нормальному закону распределения;

• отказы из-за старения материалов – закону Вейбулла.

3.4. Доверительный интервал

Статистическая величина может быть определена с заданной доверительной вероятностью точечной и интервальной оценкой вида α = α_{ср ±} 𝛥.

Точечная оценка выражается одним числом α_ср и характеризует одно наиболее вероятное значение из возможных значений случайной величины (среднее арифметическое).

Интервальная оценка (± 𝛥) задает область значений относительно точечной оценки, в которой будут находиться значения случайной величины с заданной доверительной вероятностью β.

Значение половины доверительного интервала 𝛥 вычисляется из выражения

𝛥 = t_β σ,

где t_β – значение критерия Стьюдента при заданной доверительной вероятности β (определяется по справочным таблицам); σ – величина среднего квадратического отклонения, полученная экспериментальным путем.

Контрольные вопросы

1. Что должна охватывать и что обеспечивать система сбора и обработки эксплуатационной информации?

2. Возможность решения каких задач должны обеспечить результаты сбора и обработки статистической и информации о надежности объектов?

3. Назовите четыре метод сбора информации о надежности машин в период эксплуатации.

4. Назовите пять этапов построения эмпирического распределения и статистической оценки его параметров.

5. Какая проверка производится по критерию Пирсона χ₂ (хи квадрат)?

6. Что характеризует дисперсия D?

7. Перечислите четыре основных закона распределения случайных величин в теории технической эксплуатации автомобилей и области их применения.

8. Понятие доверительного интервала.

3. Надежность сложных систем

4.1. Характеристики сложных систем

Автомобили являются сложными системами, состоящими из отдельных узлов, деталей, агрегатов и иных элементов.

Сложная система – это объект, который может быть расчленен на составляющие его элементы, каждый из которых выполняет определенные функции и находится во взаимодействии с другими элементами системы.

С точки зрения надежности сложная система обладает положительными и отрицательными свойствами. Основным фактором, отрицательно влияющим на надежность сложной системы, является большое число входящих в систему элементов, отказ каждого из которых может привести к отказу всей системы. Основным положительным свойством является, как правило, возможность восстановления работоспособности системы по частям без полного прекращения ее функционирования, например, временное отключение отдельных участков системы для их ТО и ремонта.

Соединения элементов в сложной системе могут быть последовательными, параллельными и смешанными, содержащими как последовательные, так и параллельные соединения элементов.