1. Построение эмпирического распределения и статистическая оценка его параметров

Исходной информацией, являющейся основой для построения эмпирического распределения, является таблица данных, полученных методами сбора эксплуатационной информации или в результате экспериментальных исследований рассматриваемого параметра изделия. Дальнейшая обработка данной информации производится в несколько этапов:

1. Предварительная обработка информации

В задачи предварительной обработки информации входит систематизация отказов, исключение заведомо грубых погрешностей замеров, сортировка данных по возрастанию их значений.

2. Разбивка интервалов

Ориентировочное количество интервалов К для построения гистограммы определяется из выражения:

К = 1 + 3,3 lg(n),

где n – объем выборки. При этом следует стремиться к тому, чтобы размер интервала являлся удобной для расчета круглой цифрой.

3. Построение гистограммы

Для оценки плотности вероятности отказов строится гистограмма. По оси абсцисс отложены временные интервалы (в часах) испытания изделия, а по оси ординат - количества выявленных отказов изделия в каждом из временных интервалов (плотность). На рис. 3.1 представлены примеры статистической функции плотности эмпирического распределения для экспоненциального и нормального распределений.

б

а

Рис. 3.1. Статистическая функция плотности эмпирического распределения: экспоненциальное (а) и нормальное (б) распределения. 1 - гистограмма распределения случайной величины; 2 - кривая теоретической функции распределения случайной величины

4. Подбор теоретической функции распределения случайной величины

Для имеющихся данных подбирается теоретическая функция распределения, выражающая существенные моменты распределения и исключающая случайные моменты, связанные с незначительным объемом экспериментальных данных.

Вид такой функции, как правило, зависит от вида процессов, влияющих на изменение случайной величины. Часто он определяется внешним видом гистограммы. Наиболее часто применяющиеся для аппроксимации функции рассмотрены далее в разделе «Основные законы распределения». Найденные ранее экспериментальные значения подставляют в функцию и рассчитывают ее теоретические значения в тех же интервалах.

Для нормального распределения количество отказов в интервале от - σ до + σ от среднего значения составляет 68,26 %; в интервале от - 2σ до + 2σ – 95,44 %; в интервале от - 3σ до + 3σ – 99,7 %. Если распределение отвечает указанным требованиям, то это распределение является нормальным. Данное положение называют правилом трех сигм.

Подбор теоретической функции распределения случайной величины может производиться и по рассчитанному значению коэффициента вариации V: при V = 0,10…0,33 события (отказы) могут быть описаны нормальным законом распределения; при V = 0,34…0,50 – логарифмически-нормальным распределением; при V > 0,50 - экспоненциальным распределением.

5. Проверка правильности выбора функции распределения

Проверка согласованности экспериментальных и рассчитанных по аппроксимирующей функции данных производится по критерию Пирсона χ₂ (хи квадрат).

χ₂ = ,

где P_i – экспериментально полученная частота случайной величины в интервале i; P_рi – расчетная частота случайной величины в интервале i.

Полученное расчетное значение сравнивают с табличным: χ_{2 <} χ_2табл. Если данное условие не выполняется необходимо подобрать иной закон распределения и повторить проверку.

При проведении статистической оценки параметров распределения случайной величины используются следующие основные показатели.

Среднее значение Т_ср

Т_ср =

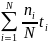
где t_i - значение, соответствующее середине i-го интервала; n_i – число отказов в данном интервале; N – число наблюдаемых объектов.

.

Дисперсия D - мера разброса данной случайной величины, то есть её отклонения от среднего значения

D = .

Среднее квадратическое отклонение σ - также как и дисперсия D является мерой разброса данной случайной величины.

σ =

Большое значение среднеквадратического отклонения или дисперсии показывает большой разброс значений в представленном множестве со средней величиной множества; маленькое значение, соответственно, показывает, что значения в множестве сгруппированы вокруг среднего значения.

Для нормального распределения количество отказов в интервале от - σ до + σ от среднего значения составляет 68,26 %; в интервале от - 2σ до + 2σ – 95,44 %; в интервале от - 3σ до + 3σ – 99,7 %. Если распределение отвечает указанным требованиям, то это нормальное распределение. Это называется правилом трех сигм.

Коэффициент вариации V - мера относительного разброса случайной величины. Показывает какую долю среднего значения этой величины составляет её средний разброс. Исчисляется в процентах. В отличие от среднего квадратического отклонения измеряет не абсолютную, а относительную меру разброса значений признака в статистической совокупности. 

V = σ/ Т_ср