Министерство образования Республики Беларусь

Учреждение образования

«Гомельский государственный университет

имени Франциска Скорины»

Заочный факультет

Кафедра «Математических проблем управления»

СУРС

по дисциплине

«Стандартизация и сертификация программного обеспечения»

«Модели надежности программного обеспечения: модель Шика - Волвертона»

Выполнил:	студент группы ПОИТ41 Каменко К.Н.
Проверила:	к-т физико-матем. наук, доцент Осипенко Н.Б.

Гомель 2015

Содержание

Введение…………………………………………………………..4

Динамические модели надежности…………………………….. 5

Модель Шика-Волвертона, ее гипотеза…………...…………… 6

Входящие и выходящие данные…………………………………8

Алгоритмы обработки данных модели…………………………10

Заключение………………………………………………………18

Список использованных источников…………………………..19

Введение

Надежность является важным и естественным требованием, предъявляемым к качеству разрабатываемых программных и информационных компонентов АСОИУ (Автоматизированные системы обработки информации и управления). Теория надежности аппаратных средств АСОИУ разработана достаточно глубоко, поэтому при исследовании надежности программного и информационного обеспечения большинство методов используют идеи теории надежности технических средств. Это позволяет инженеру не только оценивать, но и прогнозировать надежность программно-информационных продуктов.

Динамические модели надежности

В динамических моделях надежности программного средства поведение программы (появление отказов) рассматривается во времени. Для использования динамических моделей необходимо иметь данные о появлении отказов во времени.

Свойства динамических методов:

• Достоверность получаемых результатов сильно зависит от качества исходных данных. Для оценки достоверности используются метрики покрытия кода.

• При использовании прогнозных моделей обычно не учитываются влияния нерегулярных флуктуаций, имеющих место в процессе разработки и отладки ПО (особенности проекта, неравномерная плотность дефектов, квалификация персонала и др.).

Достоинства:

• Позволяют получать абсолютные показатели надежности.

Недостатки

• Высокая трудоемкость сбора исходной информации.

• Использование упрощающих предположений о взаимных влияниях программных ошибок.

• Сильная зависимость точности прогнозов от качества и объема исходной информации.

Модель Шика-Волвертона

Модификация модели Джелинского-Моранды для случая возникновения на рассматриваемом интервале более одной ошибки предложена Волвертоном и Шиком. При этом считается, что исправление ошибок производится лишь после истечения интервала времени, на котором они возникли.

Гипотеза модели.

В основе модели Шика-Волвертона лежит предположение (гипотеза), согласно которому частота ошибок пропорциональна не только количеству ошибок в программах, но и времени тестирования, т.е. вероятность обнаружения ошибок с течением времени возрастает. Частота ошибок (интенсивность обнаружения ошибок) i, предполагается постоянной в течение интервала времени ti, и пропорциональна числу ошибок, оставшихся в программе по истечении (i - 1)-го интервала; но она пропорциональна также и суммарному времени, уже затраченному на тестирование (включая среднее время выполнения программы в текущем интервале):

. (1)

В данной модели наблюдаемым событием является число ошибок, обнаруживаемых в заданном временном интервале, а не время ожидания каждой ошибки, как это было для модели Джелинского-Моранды. В связи с этим модель относят к группе дискретных динамических моделей, а уравнения для определения С и N имеют несколько иной вид:

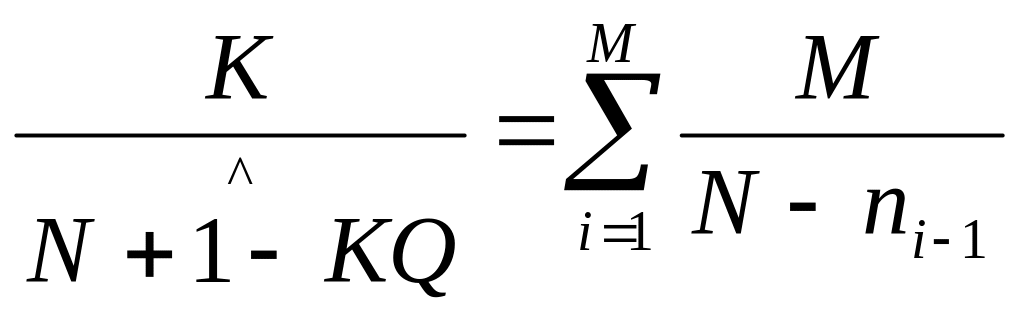, (2)

где:

t_i — продолжительность временного интервала, в котором наблюдается Мi ошибок;

Т_i-1 — время, накопленное за (i—1) интервалов:

, T₀=0 . (3)

n_i-1 — суммарное число ошибок, обнаруженных за период от первого до (i -1)-го интервала времени включительно:

, n₀=0 . (4)

М — общее число временных интервалов;

— суммарное число обнаруженных ошибок. (5)

Модель Джелинского-Моранды является частным случаем модели Шика-Волвертона для случая, когда при тестировании фиксируется время до появления очередной ошибки.