Задачи строительной механики. Связь с другими дисциплинами.
Задачи строительной механики (СМ) при расчете конструкций на прочность, жесткость и устойчивость.
СМ – дисциплина, разрабатывающая принципы и методы расчета строительных сооружений на прочность, жесткость и устойчивость.
Прочность – способность сооружения оказывать сопротивление воздействию внешних нагрузок без разрушения.
Жесткость – способность сооружения сопротивляться деформациям. Под действием нагрузки конструкция деформируется, т. е. изменяются ее форма и размеры.
Устойчивость – способность сооружения сохранять первоначальное положение и форму равновесия в деформированном состоянии.
Расчеты на прочность, жесткость и устойчивость требуют умения определять внутренние усилия в сечениях конструкций и перемещение отдельных (характерных) сечений. Задача СМ состоит в определении внутренних усилий и перемещений отдельных сечений. Для определения внутренних усилий используется метод сечений, а для определения перемещений – метод Мора.
Составление расчетной схемы сооружения.
Расчётной схемой называется упрощённое (т.е. схематическое и идеализированное) изображение реального сооружения.
К расчётной схеме предъявляются два условия:
1) Расчётная схема должна как можно ближе отвечать действительной работе сооружения;
2) Расчётная схема должна быть по возможности более простой, чтобы избежать сложных расчётов.
Упрощение осуществляется по нескольким направлениям:
1) Схематизируется геометрия элементов, связей элементов друг с другом (внутренние связи) и связи системы с основанием (внешние связи).
2) Идеализируются внешние нагрузки
3) Идеализируются свойства материала и поведение конструкции под нагрузкой.
Последнее направление осуществляется в виде гипотез.
2)Идеализация внешних нагрузок
Н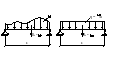
агрузки,
распределённые по небольшой поверхности,
рассматриваются как сосредоточенные.
Распределённые нагрузки (распределённые
по значительной части поверхности) по
мере возможности заменяют
равномерно-распределёнными.
Замена осуществляется на основе
статической эквивалентности обеих
нагрузок, т.е. по главному вектору и
главному моменту.
В итоге мы приходим к трём основным нагрузкам:
1) сосредоточенная сила
2
)
сосредоточенный момент
3) равномерно-распределённая нагрузка – характеризуется длиной участка действия и интенсивностью распределения. Называется так же погонной нагрузкой или нагрузкой, приходящейся на единицу времени.
При составлении уравнения равномерно-распределённая нагрузка мысленно заменяется равнодействующей, которая равна площади прямоугольника и приложена в середине прямоугольника.
Классификация сооружений.
По геометрическим признакам различают следующие виды сооружений:
1) Массивные сооружения – подпорные стены, береговые укрепления, плотины и т.д.
2) Плиты, пластины и оболочки – толщина мала по сравнению с длиной.
3) Стержневые системы – площадь поперечного сечения мала по сравнению с длиной: балки, фермы, рамы.
Стержневые системы подразделяются на плоские и пространственные.
Плоскими называются системы, у которых оси стержня, действующей нагрузки и опорных реакций расположены в одной общей плоскости.
Пространственными называются системы, для которых эти условия не соблюдаются.
Чаще всего мы встречаемся с пространственными системами. Некоторые пространственные системы разлагаются на плоские, кроме купольных.
Строительная механика изучает стержневые системы, т.е. совокупности стержней различным образом соединённых друг с другом и с основанием. Мы будем рассматривать только плоские стержневые системы.
Стержень – это одномерный элемент, у которого два размера много меньше третьего, называемого длиной.
Различают следующие основные виды соединения стержней между собой:
шарнирное:
жесткое:
комбинированное:
Устройства, соединяющие конструкцию с основанием (землей), называются опорами. Различают следующие виды опор: