9.3. Проверка коэффициента корреляции на существенность

На практике оценка связи между какими-либо показателями, как правило, осуществляется на небольшом объеме наблюдения. Такой объем наблюдения можно рассматривать как выборку. Поэтому коэффициент корреляции, рассчитанный по выборке, может не отражать истинного значения связи, которое имеет место в генеральной совокупности, и будет иметь случайное значение. Это вызывает необходимость в проверке коэффициента корреляции на его существенность (значимость).

Перед последующей проверкой полученного коэффициента корреляции необходимо, чтобы соблюдались следующие условия:

а) выборочная совокупность должна быть получена из генеральной совокупности, имеющей нормальное или близкое к нормальному распределение;

б) объем выборки должен быть меньше 30. Если объем выборки более 50 , то последующие расчеты ведутся по-другому.

Проверка полученного коэффициента корреляции на его существенность (значимость) основана на проверке нулевой гипотезы о том, что коэффициент корреляции в генеральной совокупности равен нулю или что между исследуемыми показателями нет связи, т.е. .

Вначале проверки определяется расчетное значение случайной величины по распределению Стъюдента

, (9.2)

где n – число вариантов показателей.

Затем определяется табличное значение случайной величины по распределению Стъюдента . Для этого исследователем задается уровень значимости а, рассчитывается доверительная вероятность γ=1–а и определяется число степеней свободы k=n–2. На основе γ и k по таблице (приложение 3) находится .После этого сравниваются расчетное и табличное значения.

Если , то нулевая гипотеза отвергается, коэффициент корреляции считается существенным и между показателями существует связь.

Если , то нулевая гипотеза принимается, коэффициент корреляции считается несущественным, а между показателями отсутствует связь.

По рассмотренному алгоритму осуществим проверку коэффициента корреляции, который рассчитывался с целью оценки тесноты связи между затратами на рекламу и товарооборотом.

Вначале по формуле (9.2) рассчитаем

.

Затем зададимся уровнем значимости . Напомним, что уровень значимости может быть любой, но, как правило, выбирается указанный выше. Тогда доверительная вероятность γ=1–а=1–0,05=0,95.

Определим число степеней свободы k=n–2=10–2=8. На основе рассчитанных γ и k в приложении 3 найдем табличное значение; . Если сравним между собой полученные значения и , то получим, что , так как 8,68 > 2,306. Результаты сравнения позволяют сделать вывод: с вероятностью 0,95 нулевая гипотеза может быть отвергнута, коэффициент корреляции можно считать существенным и между показателями существует связь.

9.4. Регрессионный анализ связей

Рассмотренный выше корреляционный анализ был основан на эмпирических данных. Такой подход к изучению связей между показателями не всегда дает качественный результат, поскольку эмпирическая линия регрессии отражает как функциональный (детерминированный), так и случайный характер связей по факту. Кроме того, нельзя будет рассчитать промежуточные или прогнозные значения зависимого показателя.

Чтобы выполнить этот и другие расчеты, необходимо описать корреляционную связь показателей в аналитической форме. Для этого могут быть использованы следующие уравнения регрессии (модели):

а) линейная ;

б) парабола второго порядка ;

в) показательная ;

г) степенная и другие,

где х – фактор;

– зависимый показатель;

– параметры уравнения регрессии;

– коэффициенты уравнения регрессии.

Для нахождения параметров, например, линейного уравнения регрессии может быть использован метод наименьших квадратов (МНК). На основе МНК строится система линейных уравнений

(9.3)

где n − число вариантов показателей.

Таблица 9.5

№ п/п
1	2	3	4	5
1 2 i n
Итого

Для проведения промежуточных расчетов при нахождении параметров линейного уравнения регрессии используется табл.9.5.

Решив систему линейных уравнений, найдем параметры:

; (9.4)

. (9.5)

Пример 9.2. Опишем регрессионную связь между затратами на рекламу и товарооборотом с помощью линейного уравнения регрессии . Для нахождения параметров уравнения используем данные граф 2,3 табл.9.3. А все необходимые промежуточные расчеты проведем в табл. 9.6, по итоговым данным которой и найдем параметры уравнения регрессии, используя формулы (9.4) и (9.5).

Таблица 9.6

№ п/п
1	2	3	4	5
1 2 3 4 5 6 7 8 9 10	1 2 3 4 5 6 7 8 9 10	2 2,3 3,5 3 4 4,5 4,5 4,3 5,8 7,2	1 4 9 16 25 36 49 64 81 100	2 4,6 10,5 12 20 27 31,5 34,4 52,2 72
Итого	55	41,1	385	266,2

;

.

В результате расчетов параметров уравнение регрессии будет иметь следующий вид: . Анализ параметров уравнения регрессии показывает, что с ростом на единицу затрат на рекламу объем товарооборота увеличится в среднем на 0,49 единицы объема товарооборота.

Если для описания корреляционной связи выбраны нелинейные модели (например, степенная, показательная, гипербола), то, чтобы найти параметры с помощью метода МНК, эти модели необходимо предварительно линеаризировать. Например, пусть выбрана показательная модель . Для нахождения параметров прологарифмируем ее и получим . Теперь уже с помощью МНК можно найти параметры линеаризированной модели. Промежуточные расчеты целесообразно проводить в табличной форме (см. табл.9.6) Однако в расчете будет участвовать уже не y, а lg y. С учетом этого по формулам (9.4) и (9.5) мы найдем не , а их логарифмы – . После того как мы их пропотенцируем, найдем требуемые значения , которые необходимо будет вставить в модель.

Следует отметить, что одна и та же связь между показателями может быть описана несколькими моделями, которые будут иметь разную степень аппроксимации (приближения) к исходным данным. Поэтому, чтобы выбрать оптимальную модель с позиции аппроксимации, вначале на основе здравого смысла нужно выбрать несколько типов моделей, потом рассчитать их параметры и сравнить эти модели между собой. Для выбора оптимальной модели по степени аппроксимации можно использовать критерий наименьшей суммы квадратов отклонений . Та модель, у которой этот критерий будет наименьшим, будет наилучшим образом аппроксимирована к исходным данным. Этот прием выбора наилучшей регрессионной модели является наиболее простым и может быть использован при расчете вручную.

Если использовать Excel или статистические программы, то они не только автоматически рассчитают параметры выбранного уравнения регрессии, но и определят коэффициент детерминации R². Последний можно рассматривать как оценку степени аппроксимации выбранного уравнения регрессии к исходным данным или как меру тесноты связи между фактором и зависимым показателем. В учебной литературе его еще называют теоретическим коэффициентом детерминации и обозначают η². Он изменяется в интервале [0, 1].

Коэффициент детерминации

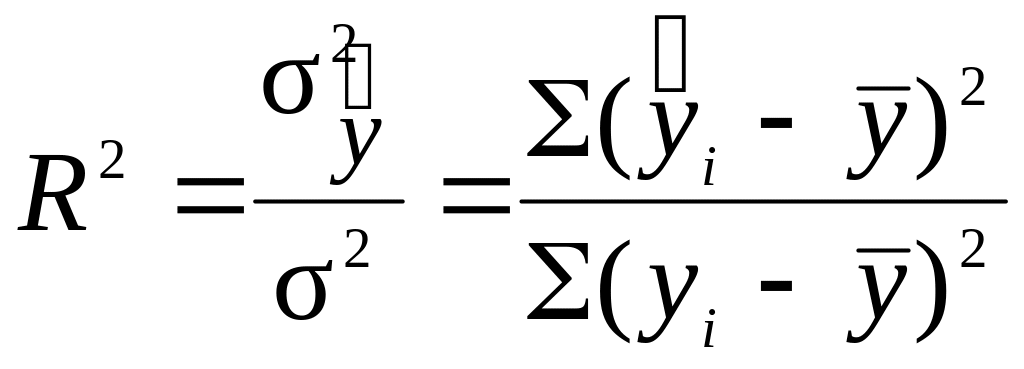; (9.6)

где −общая дисперсия зависимого показателя;

– факторная дисперсия зависимого показателя;

– среднее значение зависимого показателя, рассчитанное по фактическим данным;

y_i – i-е значение зависимого показателя по фактическим данным;

– i-е значение зависимого показателя по уравнению регрессии.

Общая дисперсия отражает изменение (вариацию) зависимого показателя под действием множества различных факторов, в том числе и фактора, который был учтен в уравнении регрессии

, (9.7)

где n– число вариантов показателей.

Факторная дисперсия отражает вариацию зависимого показателя под действие фактора, учтенного в уравнении регрессии. Формула (9.6) позволяет также интерпретировать коэффициент детерминации как долю вариации зависимого показателя, обусловленную действием фактора, учтенного в уравнении регрессии.

Факторную дисперсию можно определить следующим образом

. (9.8)

Пример 9.3 С помощью табл.9.7 проведем расчет коэффициента детерминации для рассчитанного выше уравнения регрессии, использовав данные граф 2,3 табл.9.6.

Вначале по данным графы 3 определим среднее значение зависимого показателя

.

Таблица 9.7

№ п/п
1	2	3	4	5	6
1 2 3 4 5 6 7 8 9 10	1 2 3 4 5 6 7 8 9 10	2 2,3 3,5 3 4 4,5 4,5 4,3 5,8 7,2	1,92 2,41 2,9 3,39 3,88 4,37 4,86 5,35 5,84 6,33	4,45 3,28 0,37 1,23 0,01 0,15 0,15 0,04 2,86 9,55	4,8 2,89 1,46 0,52 0,05 0,07 0,56 1,54 2,99 4,93
Итого	–	41,1	–	22,09	19,81

Затем в графе 4 определим значения зависимого показателя по рассчитанному уравнению регрессии .

Для этого в уравнение будем последовательно подставлять значения х из графы 2. Так, для первой строки графы 4 зависимый показатель по уравнению

регрессии

, для второй строки графы 4 и т. д.

На следующем шаге определим значения показателя графы 5, используя данные графы 3 и среднее значение зависимого показателя (4,11). Так, для первой строки , для второй строки и т.д.

Теперь заполним графу 6 по данным графы 4 и среднему значению зависимого показателя (4,11). Так, для первой строки , для второй строки и т.д.

В заключении определим коэффициент детерминации по формуле (9.6)

.

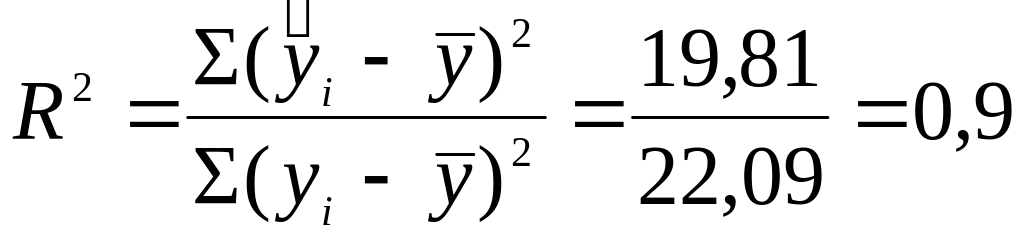Он показывает, что между затратами на рекламу и товарооборотом существует тесная связь, а доля вариации товарооборота, обусловленная фактором затрат на рекламу, составляет 90%. Если мы рассчитаем коэффициент детерминации для другого уравнения регрессии (например, для показательного уравнения регрессии), то после сопоставления коэффициентов можем определить, какая из выбранных моделей наилучшим образом аппроксимирована к исходным данным.