9.2. Методы выявления корреляционной связи и их оценка

Выявление связи между и , как правило, начинается с применения графического метода. Он основан на построении корреляционного поля, где на оси абсцисс откладывается фактор , а на оси ординат – зависимый показатель . Затем на основе исходных данных на корреляционном поле откладываются точки с координатами ( , ). По характеру расположения точек на корреляционном поле делается предварительный вывод о наличии или отсутствии корреляционной связи между анализируемыми показателями.

Пример 9.1. Маркетинговая служба АО "Модная обувь" решила выяснить, есть ли наличие корреляционной связи между затратами на рекламу (фактор), которые осуществляет АО, и товарооборотом (зависимый показатель). Для этого были обследованы 30 филиалов АО. Результаты статистического наблюдения (в условных единицах) были сведены в табл. 9.1.

Таблица 9.1

Показатель	№ филиала
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Затраты на рекламу Товарооборот	1 1	6 3	3 5	9 4	2 4	1 3	5 5	10 5	2 2	7 2	5 2	9 7	4 2	10 9	4 4

Окончание табл.9.1

Показатель	№ филиала
	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
Затраты на рекламу Товарооборот	8 6	9 3	6 8	2 1	10 8	9 9	7 7	3 2	5 3	8 2	10 7	5 6	6 2	6 5	8 5

На основе данных табл. 9.1. построим корреляционное поле связи затрат на рекламу и товарооборота (рис.9.4).

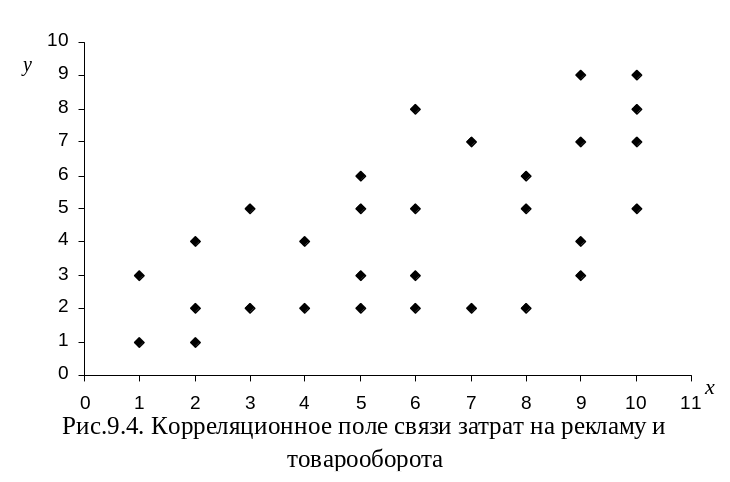
Изучение расположения точек на корреляционном поле позволяет сделать вывод о том, что с ростом затрат растет в среднем и товарооборот, а это говорит о наличии корреляционной связи между затратами на рекламу и товарооборотом.

Другим методом выявления корреляционной связи между показателями является метод аналитических группировок. Сущность его заключается в том, что на основе данных о факторе и зависимом показателе осуществляется их (данных) структурная группировка. Принципы группировки изложены в учебном пособии по статистике [1]. Затем по каждой группе рассчитываются средние значения.

С учетом структурной группировки строится статистическая таблица, где в подлежащем располагаются группы фактора (например, затраты на рекламу), в сказуемом – группы зависимого показателя (например, товарооборот), а в ячейках таблицы показывается число единиц совокупности (число филиалов), у которых значения фактора и зависимого показателя попадают в определенный интервал фактора и зависимого показателя.

Поскольку в нашем примере фактор имеет небольшое (10) число значений (вариант), то мы не будем проводить группировку данных, а сразу для каждого значения фактора (затраты на рекламу) рассчитаем среднее значения товарооборота. Исходя из данных табл. 9.1, можно отметить, что затраты на рекламу по одной условной единице имеют филиалы № 1 и 6, у которых товарооборот, соответственно, равен 1 и 3 усл. ед. Тогда средний товарооборот при данных затратах на рекламу можно определить с помощью простой средней арифметической

.

Затраты на рекламу, равные 2 усл. ед., имеют филиалы № 5; 9 и 19, у которых товарооборот, соответственно, равен 4, 2 и 1 усл. ед. Тогда средний товарооборот при данных затратах на рекламу

.

Аналогичным образом рассчитаем средний товарооборот и для других значений затрат на рекламу. Результаты расчетов сведем в табл. 9.2.

Таблица 9.2

Затраты на рекламу	1	2	3	4	5	6	7	8	9	10
Средний товарооборот	2	2,3	3,5	3	4	4,5	4,5	4,3	5,8	7,2

Теперь по данным табл.9.2 построим график (рис. 9.5), где на оси абсцисс отложим значения фактора (затрат на рекламу), а на оси ординат – соответствующие значения среднего товарооборота.

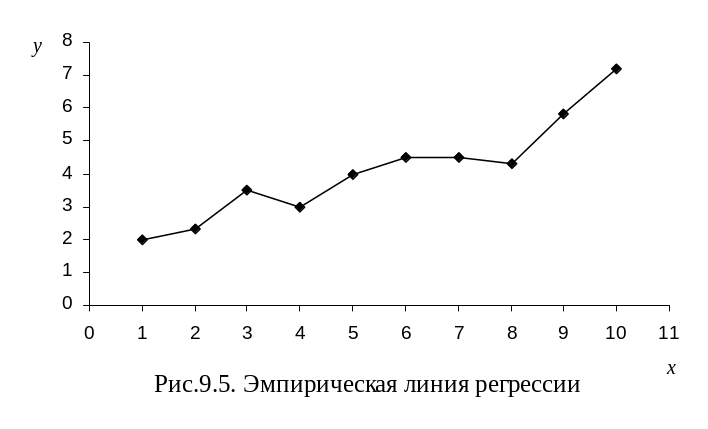
Полученная ломаная линия называется эмпирической линией регрессии. Она показывает, как в среднем изменяется товарооборот при изменении затрат на рекламу. Можно также отметить, что между затратами на рекламу и товарооборотом существует прямая корреляционная связь, так как с ростом затрат на рекламу растет в среднем и товарооборот.

После того как на логическом уровне было установлено, что между фактором и зависимым показателем существует корреляционная связь, необходимо количественно оценить тесноту этой связи. Для этого используем коэффициент Фехнера и линейный (парный) коэффициент корреляции.

Для определения тесноты связи между фактором (затратами рекламу) и зависимым показателем (товарооборот) с помощью коэффициента Фехнера построит таблицу (табл.9.3).

Таблица 9.3

№ п/п	Затраты на рекламу хi	Средний товарооборот			Оценка совпадения знаков
1	2	3	4	5	6
1 2 3 4 5 6 7 8 9 10	1 2 3 4 5 6 7 8 9 10	2 2,3 3,5 3 4 4,5 4,5 4,3 5,8 7,2	– – – – – + + + + +	– – – – – + + + + +	С С С С С С С С С С
Итого	55	41,1	–	–	–

В графах 2 и 3 определим итоговые значения. Затем рассчитаем средние значения фактора (затраты на рекламу) и зависимого показателя (средний товарооборот) с помощью средней арифметической простой

.

В графе 4 отметим знаки отклонения конкретного значения фактора (затраты на рекламу) от его средней величины. Так, для первой строки знак отклонения соответствует "минусу" (–) , так как . Для второй сроки знак отклонения также соответствует "минусу" (–), потому что . И так далее. В графе 5 отметим знаки отклонения конкретного значения зависимого показателя (средний товарооборот) от своей средней величины. Так, для первой строка знак отклонения соответствует "минусу" (–), так как . Для второй строки знак отклонения также соответствует "минусу" (–), поскольку и т.д.

В графе 6 проставим оценку совпадения знаков. Если знаки в графах 4 и 5 по строкам совпадают, то в соответствующих строках графы 6 ставим знак С, если знаки по строкам не совпадают, то ставим знак Н. Затем для графы 6 определим общее число знаков и знаков . Сравнивая по первой строке знаки в графах 4 и 5, мы видим, что они совпадают (в обоих случаях это "минусы"). Следовательно, в первой строке графы 6 ставим знак С и т.д.

В нашем примере по всем строкам знаки совпали и их общее число равно 10, т.е. . Поскольку в графе 6 нет ни одного символа Н, то . Теперь определим степень тесноты связи между фактором и зависимым показателем с помощью коэффициента Фехнера

.

Коэффициент Фехнера изменяется от −1, когда имеется обратная функциональная связь между фактором и зависимым показателем, в этом случае , до +1, когда имеется прямая функциональная связь между фактором и зависимым показателем, в этом случае . Если , то и между фактором и зависимым показателем нет никакой связи (случайная связь).

Рассчитанный коэффициент Фехнера показывает, что между фактором и зависимым показателем практически существует прямая функциональная связь.

Другим средством оценки тесноты связи является линейный (парный) коэффициент корреляции. Он используется тогда, когда связь между фактором и зависимым показателем представляет собой линейную зависимость. Данный коэффициент корреляции

. (9.1)

На основе данных граф 2 и 3 табл. 9.3 проведем вычисления и заполним табл. 9.4.

По формуле 9.1 и итоговым данным табл.9.4 определим линейный коэффициент корреляции

.

Таблица 9.4

№ п/п							( )( )
1	2	3	4	5	6	7	8
1 2 3 4 5 6 7 8 9 10	1 2 3 4 5 6 7 8 9 10	2 2,3 3,5 3 4 4,5 4,5 4,3 5,8 7,2	−4,5 −3,5 −2,5 −1,5 −0,5 0,5 1,5 2,5 3,5 4,5	20,25 12,25 6,25 2,25 0,25 0,25 2,25 6,25 12,25 20,25	−2,11 −1,81 −0,61 −1,11 −0,11 0,39 0,39 0,19 1,69 2,89	4,45 3,28 0,37 1,23 0,01 0,15 0,15 0,04 2,86 8,35	9,5 6,34 1,53 1,67 0,06 0,2 0,59 0,48 5,92 13,01
Итого	55	41,1	–	82,5	–	20,89	39,3

Рассчитанный линейный коэффициент корреляции дает более точную оценку тесноты связи между фактором и зависимым показателем. Практическое совпадение значения обоих показателей (коэффициента Фехнера и линейного коэффициента корреляции) говорит об объективности полученных оценок.

Коэффициент линейной корреляции изменяется от −1 до +1. Их интерпретация совпадает с тем, что было дано для коэффициента Фехнера. На основе промежуточных значений коэффициента линейной корреляции можно дать качественную оценку связи следующим образом:

а) если , то связи нет или она нелинейна;

б) если , то связь считается слабой;

в) если , то связь считается средней;

г) если , то связь считается сильной.

С учетом отмеченного подхода к оценке тесноты связи можно считать, что между затратами на рекламу и товарооборотом существует сильная связь.