54. Способы корректировки гетероскедастичности. Доступный метод взвешенных наименьших квадратов.

В соответствии со второй предпосылкой теоремы Гаусса-Маркова нужно соблюдение условия гомоскедастичности, или однородности, или одинаковости дисперсий случайных возмущений во всех наблюдениях: . Если это условие не соблюдается, то имеет место гетероскедастичность. Распределение u для каждого наблюдения имеет нормальное распределение и нулевое ожидание, но дисперсия распределений различна. Последствия нарушения условия гомоскедастичности случайных возмущений: 1. Потеря эффективности оценок коэффициентов регрессии, т.е. можно найти другие, отличные от МНК и более эффективные оценки. 2. Смещенность стандартных ошибок коэффициентов в связи с некорректностью процедур их оценки. Это, в свою очередь, может привести к некорректности результатов тестирования статистической значимости параметров линейной модели.

Подход к решению проблемы устранения гетероскедастичности сводится к искусственному преобразованию спецификации модели таким образом, чтобы условие гомоскедастичности выполнялось тождественно. Пусть спецификация модели: Yt=a₀+a₁x_1t+a₂x_2t+a₃x_3t+u_t

Взвешенный метод наименьших квадратов: Предполагается, что дисперсию случайного возмущения можно представить в виде:

где: – дисперсия единицы веса, λ – заданная константа, например ±0.5; ±1; ±2. Вес случайного остатка вычисляется по правилу: . Если в схеме Гаусса-Маркова не выполняется предпосылка о гомоскедастичности случайных возмущений, то наилучшей линейной процедурой оценки параметров модели является: . где: Р матрица ковариаций случайных возмущений в уравнения наблюдений:

55. Обобщенная регрессионная модель. Обобщенный метод наименьших квадратов.

Обобщенная регрессионная модель имеет следующую спецификацию:

Здесь

вектор-столбец значений эндогенной переменной,

– детерминированная матрица регрессоров полного ранга,

– вектор-столбец параметров модели,

– вектор-столбец случайных возмущений.

Относительно случайных возмущений регрессии принимают следующие предполсылки:

1. 

2. – автоковариационная матрица возмущений,

3. 

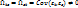
То есть 2-ая и 3-я предпосылки Гаусса-Маркова нарушены.

Преобразование переменных

Матрица преобразований:

Оцениваемая спецификация:

Числовые характеристики случайного возмущения преобразованной модели:

1. Мат ожидание:

2. Автоковариационная матрица СВ:

ОМНК-оценка вектора параметров. Оценка Айткена.

Числовые характеристики ОМНК-оценок вектора параметра.

1. Мат. ожидание:

2. Автоковариационная матрица:

Критерий отбора ОМНК:

Минимизируется “обобщенная” сумма квадратов отклонений.

Условия применения ОМНК:

Элементы автоковариационной матрицы вектора возмущений известны.

56. Спецификация и оценивание мнк эконометрических моделей нелинейных по параметрам.

На практике большинство моделей отражают экономические процессы в виде нелинейной зависимости.

Регрессией, нелинейной по оцениваемым параметрам, например, является степенная функция (5), в которой сама степень является параметром и зависит от него.

Среди нелинейных функций, которые могут быть приведены к линейному виду, в эконометрических исследованиях очень широко используется степенная функция (5).

(5)

Данное соотношение легко преобразовать в линейное уравнение с помощью логарифмирования (5):

(6)

После введения новых переменных, обозначающих логарифмы, получается линейное уравнение (6). Тогда процедура оценивания регрессии состоит в вычислении новых переменных для каждого наблюдения путём взятия логарифмов от исходных значений.

(7)

Затем оценивается регрессионная зависимость новых переменных. Для перехода к исходным переменным следует проэкспонировать полученные показатели. Аналогично можно рассматривать случай показательных или экспоненциальных функций.

показательная ; (8)

экспоненциальная . (9)

Класс регрессий, нелинейных по оцениваемым параметрам, в свою очередь, делится на два подкласса: к одному относятся внешне нелинейные, но по существу внутренне линейные. В этом случае можно привести модель к линейному виду с помощью преобразований. Данные модели были рассмотрены ранее. Однако, если модель внутренне нелинейная, то она не может быть сведена к линейной функции.