2.3. Преобразование схем замещения

Для определения результирующего сопротивления короткозамкнутой цепи схему замещения СЭС приводят к простейшему виду путем эквивалентных преобразований. При этом могут быть использованы следующие способы преобразований и расчета:

1. Объединение точек равного потенциала.

2. Разрезание узла трехфазного КЗ.

3. Эквивалентирование с заменой последовательно и параллельно соединенных ветвей схемы замещения одной эквивалентной ветвью.

4. Замена нескольких источников с разными ЭДС и сопротивлениями, присоединенных к общей точке сети, одним эквивалентным источником.

5. Преобразование сопротивлений, соединенных в звезду, в сопротивления, соединенные в треугольник, и наоборот. Обычно такими преобразованиями пользуются после преобразований последовательно и параллельно соединенных ветвей.

6. Преобразование многолучевой звезды в полный многоугольник с диагоналями.

7. Применение метода наложения, с помощью которого решение получают как результат суммы ряда действительных режимов, каждый из которых определяется при условии, что в схеме приложена одна ЭДС, а остальные равны нулю.

8. Определение коэффициентов токораспределения по ветвям схемы от разных источников. (В этом методе определяют долю от каждого источника питания). Данный метод используется для сложных схем при необходимости применения различных методов для определения тока КЗ по разным ветвям. Например, для выделения ветви с системой ограниченной или неограниченной мощности и ветви с генераторами, при определении тока КЗ в определенный момент времени. В этом случае при преобразовании наряду с упрощением схемы замещения также можно определить роль каждого источника в питании точки КЗ.

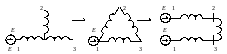
Рис. 1. Преобразование трехлучевой звезды с ЭДС в разрезанный треугольник

9. Иногда преобразования схемы замещения заметно упрощаются, если трехлучевую звезду с ЭДС в одном луче заменить треугольником, затем разрезать по вершине, где приложена ЭДС. Образовавшиеся параллельные ветви заменяют эквивалентными с ЭДС такого же значения (рис. 1). Возможно и обратное преобразование.

2.4. Электромагнитные переходные процессы в простейшей цепи при её питании от источника бесконечной мощности

Простейшая трехфазная цепь – это симметричная трехфазная цепь, с сосредоточенными активными и индуктивными сопротивлениями при отсутствии в ней трансформаторных связей (рис. 2).

Источник бесконечной мощности – источник, собственное сопротивление которого равно нулю. Его напряжение, изменяясь с постоянной частотой, имеет неизменную амплитуду:

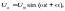
где 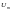– амплитуда напряжения источника; t – момент времени; α – фаза включения, которая фиксирует момент возникновения КЗ.

i_c

U_c L r_k L₁ r₁

i_b

U_b L r_k L₁ r₁

i_a

U_a L r_k L₁ r₁

B

Рис. 2. Простая трехфазная цепь

После включения выключателя B цепь распадается на два участка. В правой части цепи после КЗ энергия, запасенная в индуктивности L₁, будет переходить в тепло, поглощаясь сопротивлением r₁, при этом в дифференциальном уравнении равновесие для каждой фазы участка можно записать так:

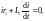
его можно решить относительно тока:

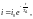
где Т_а1 – постоянная времени цепи, она определяется исходя из сопротивлений:

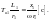
В левом участке схемы будет продолжаться переходный процесс за счет имеющегося питания со стороны источника, т. е. в этом участке будет существовать принужденный ток. Он будет сдвинут на некоторый угол относительно предшествовавшего тока.

Дифференциальное уравнение относительно фазы А:

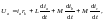
Так как можно записать:

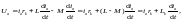
где L_k = L– M – результирующая индуктивность фазы с учетом влияния других фаз.

В общем виде для любой фазы:

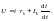(1)

Решение уравнения (1) будет:

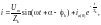(2)

где 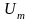– максимальное амплитудное значение фазного напряжения источника, принимается средним номинальным для ступени КЗ; Z_k – полное сопротивление цепи КЗ; ω – угловая частота напряжения источника, определяемая по формуле 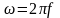; t – время; α – фаза возникновения КЗ, фиксирует момент возникновения КЗ (если не задана, можно взять равной нулю); φ_k – угол сдвига по фазе периодической составляющей тока КЗ относительно напряжения; Т_а – постоянная времени цепи КЗ:

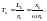
В уравнении (2) ток i – это сумма двух слагаемых:

1) принужденный ток или периодическая слагающая тока КЗ,

2) свободная составляющая или апериодическая составляющая тока КЗ.

То есть полный ток КЗ можно записать как:

Начальное значение тока КЗ (t = 0):

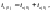
отсюда

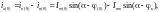(3)

где 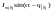– полный ток предшествующего режима; 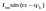– периодическая составляющая тока КЗ; 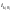– начальное значение 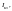которое с учетом невозможности изменения тока скачком в цепи с индуктивностью равно 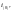т. е. току предшествующего режима в данной фазе к моменту

На векторной диаграмме [3] 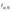является проекцией 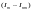на ось времени.

В зависимости от фазы включения КЗ начальное значение может меняться. Его значение будет максимальным, если в момент включения КЗ разность векторов будет параллельна оси t, т. е.:

1) при α = 0 и отсутствии предшествовавшего тока в цепи,

2) при х_k >> r_k, то есть когда в цепи преобладает индуктивность, имеем 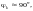в этом случае будет возникать наибольший апериодический ток и будет достигнут максимум мгновенного значения тока КЗ (рис. 3).

Максимальное мгновенное значение 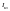называется ударным током 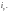Считают, что он наступает примерно через полпериода (Т/2). При f = 50 Гц Т/2 = 0,01 с с момента возникновения КЗ.

С учетом вышеуказанных условий, т. е. 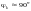и α = 0,

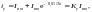(4)

где 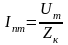– амплитуда периодической составляющей тока КЗ в начальный момент времени; 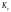– ударный коэффициент, показывающий превышение ударного тока над амплитудой периодической слагающей

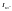
Ударный коэффициент в этом случае можно определить по формуле:

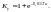(5)

Ударный коэффициент лежит в пределах:

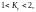
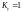при при

T/2

Норм.

режим

Рис. 3. Изменение полного тока и его составляющих

Чем меньше Т_а, тем быстрее затухает i_a, следовательно, тем меньше К_y. Влияние i_a сказывается лишь в начальный момент переходного процесса, т. к. в сетях и установках высокого напряжения i_a затухает через 0,1–0,3 с, а в установках низкого напряжения она практически незаметна.

При увеличении в цепи доли активного сопротивления, в частности при Х/R < 5 использование формулы (5) для определения ударного коэффициента даст существенную погрешность, поэтому для более точного его определения можно воспользоваться рекомендациями в 3.4 или [1].