Методология выявления тренда в динамических рядах
Нахождение основной тенденции изменения уровней динамического ряда предполагает ее количественное выражение, в определенной степени свободное от воздействия случайных факторов.
Выявление основной тенденции развития (тренда) называется в статистике выравниванием.
Методы выявления основной тенденции динамического ряда априори
1) По существу изучаемых явлений (теоретический анализ).
2) Построение графического изображения.
3) Механический метод:стр 430
метод укрупнения интервалов;
усреднение полученных укрупненных уровней за ряд лет;
сглаживание по скользящей средней.
4) Проверка гипотезы о различии средних показателей динамики:
дисперсионный анализ (если ряд разбит на 3-5 периодов);
в различных частях динамического ряда (если ряд разбит на 2 части).
Механический метод
метод укрупнения интервалов (первоначальный ряд заменяется другим, уровни которого характеризуются значительно большими по продолжительности времени значениями);
усреднение полученных укрупненных уровней за ряд лет;
сглаживание по скользящей средней (объединение отдельных периодов в группы и исчисления средних, но со сдвигом на один, два или более периодов).
Интервал сглаживания желательно выбирать по нечетному числу уровней, то есть 3, 5, 7 и т. д.
Аналитическое выравнивание - метод измерения параметров тренда
Прослеживая (обычно на графике) развитие отдельного социально-экономического явления за ряд лет, можно подобрать теоретическую кривую (аналитическую функцию), достаточно хорошо аппроксимирующую эмпирический ряд.
прямую;
параболу;
экспоненту;
логарифмическую кривую и др.
Метод аналитического выравнивания
Рассмотрим
аналитическое выравнивание ряда динамики
по прямой:
,
где t - порядковый номер периода или момента времени.
Методом наименьших квадратов рассчитываются параметры а и b на основе системы нормальных уравнений:
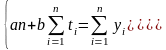
Метод аналитического выравнивания
Нахождение параметров а и b упрощенным способом, при котором переносят начало координат в середину динамического ряда:
откуда:
,
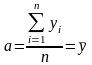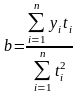
Апостериорная проверка правильности выбранного типа тренда
1) Проверка значимости найденных параметров уравнения.
2) Проверка на основе суммы квадратов отклонений фактических значений от теоретических (рассчитанных по тренду). Из совокупности кривых выбирается та, которой соответствует минимальное значение критерия (данная проверка производится по уравнениям, имеющим одинаковое число параметров).
45 Интерполяция и экстраполяция уровней динамического ряда
При изучении длительной динамики иногда возникает необходимость определения неизвестных уровней внутри ряда динамики.
Интерполяцией называется приблизительный расчет недостающих уровней внутри однородного периода, когда известны прилегающие по обе стороны уровни.
Экстраполяцией называется расчет недостающего уровня, когда известен уровень только по одну сторону. Если рассчитывается уровень в сторону будущего, это называется перспективной экстраполяцией, в сторону прошлого - ретроспективной экстраполяцией.
Как интерполяция, так и экстраполяция должны производиться в период действия одной закономерности. Предполагается, что закономерность развития, найденная внутри ряда, сохраняется.
Приемы расчета неизвестного уровня зависят от характера изменения исследуемого явления. При плавном характере изменения уровня можно недостающий уровень определить: полусуммой двух прилегающих уровней, по среднему абсолютному приросту, по среднему коэффициенту роста.
Так, по среднему абсолютному приросту неизвестный уровень (как при интерполяции, так и при экстраполяции) определяется как
,
(14.16)
по
среднему коэффициенту роста: 
(14.17)
Если в ряду динамики отмечаются резкие колебания, то лучше применять средний абсолютный прирост или средний темп роста за весь период исследования, как указано в формулах. Что использовать – абсолютный прирост или темп роста? Для этого необходимо рассчитать показатели (цепные) по исходному ряду динамики, и который из рядов окажется более устойчивым, по нему и следует провести интерполирование или экстраполирование как по смежным, так и по средним значениям уровней.