Оценка тесноты связи нелинейной зависимости
При наличии нелинейной зависимости
(парабола, гипербола, экспонента и т.п.)
теснота связи оценивается эмпирическим
корреляционным отношением
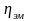
или
Теоретическое корреляционное отношение
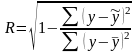
В случае, если
или
,
можно говорить о том, что связь между
признаками линейная.
Уравнения регрессии
Расчет
дополняется определением параметров
уравнения регрессии методом наименьших
квадратов.
1) Парная линейная регрессия:
2) Параболическая регрессия:
3) Гиперболическая регрессия:
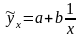
4) Показательная регрессия:
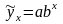
5) Логарифмическая регрессия:
В парной линейной регрессии значение параметра b показывает, на сколько единиц изменяется в среднем у с изменением х на единицу,
Коэффициент детерминации
показывает, какая доля вариации
результативного признака у
обусловлена изменением факторного
признака х.
Коэффициент эластичности
Коэффициент эластичности при линейной зависимости определяется по формуле:
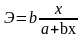
Он показывает на сколько процентов в среднем изменится значение результативного признака при изменении факторного признака на один процент, т. е. представляет собой соотношение темпов прироста у и х.
Оценка существенности коэффициента регрессии
Проверка адекватности моделей, построенных на основе уравнений регрессии, начинается с проверки значимости каждого коэффициента регрессии.
Значимость коэффициентов регрессии осуществляется с помощью t-критерия Стьюдента
,
где
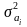-дисперсия коэффициента регрессии
Коэффициент регрессии
Коэффициент регрессии признается
статистически значимым, если
,
где α - уровень значимости критерия проверки гипотезы о равенстве нулю параметров, измеряющих связь,
v = n-к-1 - число степеней свободы, которое характеризует число свободно варьирующих элементов совокупности.
Оценка существенности уравнения связи
Проверка адекватности всей модели
осуществляется с помощью расчета
F-критерия и величины средней ошибки
аппроксимации
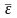
Если
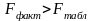при
заданном уровне значимости, то гипотеза
о несоответствии заложенных в уравнении
регрессии связей отвергается.
,
где
- совокупный коэффициент множественной
детерминации.
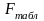определяется по таблицам на основании
уровня значимости и числа степеней
свободы:
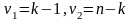
где n - число наблюдений, k - число факторных признаков в уравнении.
Значение средней ошибки аппроксимации определяется по формуле:
,
где - средняя ошибка аппроксимации, и не должно превышать 12-15 %.
Множественная корреляция
,
где a,b,c, ...d - коэффициенты регрессии,
,
,
...
-
факторные признаки
Совокупный коэффициент множественной корреляции
При наличии трех признаков x, z, y один из которых рассматривается как результативный (у), рассчитывается коэффициент множественной корреляции
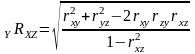
компоненты которого (парные коэффициенты корреляции) определяются по указанным выше формулам.
Пределы изменения совокупного коэффициента
множественной корреляции:
Надежность совокупного коэффициента множественной корреляции определяется по формуле:
,
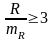где
где N - число наблюдений, n - число факторов
Парциальные (частные) коэффициенты корреляции
При изучении зависимости явлений приобретает особое значение необходимость устранения влияния какого-либо фактора. Это достигается помимо построения и анализа комбинационных таблиц путем применения метода частной корреляции. Он заключается в построении частных (парциальных) коэффициентов корреляции.
Парциальные коэффициенты исчисляются на основе парных коэффициентов корреляции по формулам:
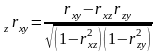
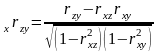
имеют границы:
Применение: Оценка хозяйственной деятельности по отклонениям от расчетных значений показателей на основе уравнений регрессии (тем более на основе многофакторных регрессионных моделей) гораздо более оправдана и содержательна, чем оценка результатов производства по отклонениям от среднего значения результативного признака в совокупности без учета факторов - характеристик возможностей и природных условий предприятия.