
- •Тема 11. Статистическое изучение корреляционных взаимосвязей
- •Связь изучается между вариацией результативного и факторного признаков, а не между их отдельными величинами
- •Коэффициенты Фехнера и Спирмэна
- •Эмпирическое и теоретическое корреляционное отношение
- •Оценка тесноты связи нелинейной зависимости
- •Множественная корреляция
- •38 Ранговый коэффициент корреляции, коэффициент корреляции Фехнера
- •39 Построение параллельных рядов и количественная оценка их взаимосвязи
- •Показатели тесноты связи качественных признаков
- •Динамические ряды, основные элементы и правила их построения
- •Абсолютные и относительные показатели динамики
- •Средние величины в динамических рядах
- •Методология выявления тренда в динамических рядах
- •45 Интерполяция и экстраполяция уровней динамического ряда
- •46 Понятие о сезонных колебаниях. Индексы сезонности, их расчет и графическое изображение.
- •47 Индексный метод в экономико-статистическом анализе
- •Формулы индексов
- •Г рафик Варзара
- •Статистические графики
- •Виды статистических графиков
- •Статистические графики
- •55. Нормальное распределение.
- •Свойства нормального распределения
- •Косвенные расчеты показателей вариации
- •Критерий согласия к.Пирсона
- •Критерий согласия в. И. Романовского
- •Критерий согласия б.С.Ястремского
- •Критерий согласия а.Н.Колмогорова
- •58. Коэффициенты ассиметрии и эксцесса
- •Оценка существенности асимметрии
- •Эксцесс распределения
- •Оценка существенности эксцесса
Критерий согласия в. И. Романовского
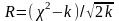 ,
где k- число степеней свободы
,
где k- число степеней свободы
Если R<3, расхождения между теоретическими и эмпирическими частотами считаются случайными,
Если R>3, то неслучайными, существенными.
Критерии согласия Пирсона и романовского не показывают, чем конкретно отличаются рассматриваемые распределения. С этой целью применяются специальные показатели асимметрии и эксцесса.
Критерий согласия б.С.Ястремского
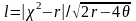 ,
где r- число групп.
,
где r- число групп.
Величина
 имеет табличное значение, равное 0,6 для
распределений, где число групп представлено
до 20.
имеет табличное значение, равное 0,6 для
распределений, где число групп представлено
до 20.
Если
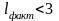 ,
расхождение между теоретическими и
эмпирическими распределениями считаются
случайными;
,
расхождение между теоретическими и
эмпирическими распределениями считаются
случайными;
Если
 ,
расхождение между теоретическими и
эмпирическими распределениями неслучайны,
то есть эмпирические распределение не
отвечает требованиям нормального
распределения.
,
расхождение между теоретическими и
эмпирическими распределениями неслучайны,
то есть эмпирические распределение не
отвечает требованиям нормального
распределения.
Критерий согласия а.Н.Колмогорова
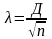
Вероятность
Р(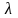 )
может изменяться от 0 до 1.
)
может изменяться от 0 до 1.
Если принимает значения до 0,3, то Р( )=1, следовательно отклонений между эмпирическими и теоретическими частотами нет.
58. Коэффициенты ассиметрии и эксцесса
Показатели формы распределения
Асимметрия – Коэффициент асимметрии характеризует асимметричность («скошенность») распределения признака в совокупности
Эксцесс – Показатель эксцесса представляет собой отклонение вершины эмпирического распределения вверх или вниз («крутость») от вершины кривой нормального распределения
Асимметрия распределения
При =0 распределение считается нормальным.
При > 0 правосторонняя асимметрия.
При <0 левосторонняя асимметрия.
Если асимметрия более 0,5, то независимо от знака она считается значительной
Если асимметрия меньше 0,25, то она считается незначительной

Асимметрия распределения рассчитанная по формулам К.Пирсона: |
|
|
является приблизительной |
Расчет асимметрии распределения при помощи нормированного момента третьего порядка дает наиболее точный результат |
|
т.е.
- нормированный момент третьего порядка |
Показатель Пирсона зависит от степени асимметричности в средней части ряда распределения, а показатель асимметрии, основанный на моменте третьего порядка, - от крайних значений признака.
Оценка существенности асимметрии
Для оценки существенности асимметрии вычисляют показатель средней квадратической ошибки коэффициента асимметрии

Если
отношение
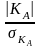 имеет значение больше 2, то это
свидетельствует о существенном характере
асимметрии
имеет значение больше 2, то это
свидетельствует о существенном характере
асимметрии
Эксцесс распределения
Показатель эксцесса представляет собой отклонение вершины эмпирического распределения вверх или вниз («крутость») от вершины кривой нормального распределения, НО! График распределения может выглядеть сколь угодно крутым в зависимости от силы вариации признака: чем слабее вариация, тем круче кривая распределения при данном масштабе. Не говоря уже о том, что, изменяя масштабы по оси абсцисс и по оси ординат, любое распределение можно искусствен но сделать «крутым» и «пологим». Чтобы показать, в чем состоит эксцесс распределения, и правильно его интерпретировать, нужно сравнить ряды с одинаковой силой вариации (одной и той же величиной σ) и разными показателями эксцесса. Чтобы не смешать эксцесс с асимметрией, все сравниваемые ряды должны быть симметричными. Такое сравнение изображено на рис.

Поскольку эксцесс нормального распределения равен 3, показатель эксцесса вычисляется по формуле
|
или
|
где
|
При >0 – высоковершинный эксцесс распределения
При <0 – низковершинный эксцесс распределение
При =0 – нормальное распределение




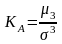
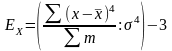

 -
нормированный момент четвертого
порядка
-
нормированный момент четвертого
порядка