Магічні квадрати

Магічні квадрати є одним із найбільш відомих видів крос-сум. Для заповнення їх рядків і стовпчиків не потрібно задавати різні умови як для заповнення кроснамберів, оскільки основна властивість магічних квадратів: суми натуральних чисел, що не повторюються, у кожному рядку, у кожному стовпчику і у кожній із двох діагоналей однакові. Тобто загальну задачу для

побудови магічних квадратів можна сформулювати так: дані числа розставити у клітинках квадрата так, щоб у рядках, стовпчиках і діагоналях утворилися однакові суми.

Зауважимо, що за таким принципом побудовано більшість магічних квадратів, але є й інші. Наприклад, потрібно розставити у клітинках квадрата

натуральні числа, що не повторюються, так, щоб добутки чисел кожного рядка, кожного стовпчика і кожної з двох діагоналей були однакові.

Також зустрічаються завдання, коли у клітинки квадрата потрібно розставляти групи однакових чисел.

Під час розгляду цієї теми на заняттях математичного гуртка доречно завдання на заповнення магічних квадратів поєднати з історичними відомостями про їх виникнення. Згодом (у 7—8-х класах або в 9-му класі під

час вивчення арифметичної прогресії) слід розглянути теоретичні аспекти побудови магічних квадратів, зокрема парних (4 х 4,8 х 8,12 х 12) і непарних (3 х 3, 7 х 7) порядків.

Із історії магічних квадратів. Оскільки перша згадка про магічні квадрати зустрічається в китайській книзі, написаній за 4000—5000 років до н.е., то напевно саме китайцям і належить їх винахід.

У найстарішому в світі китайському магічному квадраті чорними кружечками зображені парні числа (жіночі), а білими кружечками — непарні (чоловічі). А сам квадрат зображено на рис. 33.

У звичному запису цей квадрат має вигляд, зображений на рис. 34.

Іншою пам’яткою давнини є індійський магічний квадрат 4x4, датований І ст. н. е. У ньому 16 чисел від 1 до 16, розміщені в 16 клітинках квадрата так, що виконується основна властивість магічного квадрата.

1	14	15	4
12	7	6	9
8	11	10	5
13	2	4	16

Кожне число магічного квадрата бере участь у двох сумах (сума чисел, що стоять у рядку, і сума чисел, що стоять у відповідному стовпчику), а числа, які розміщені по діагоналях – у трьох сумах, і всі суми дорівнюють 34. Число 34 називають магічною константою.

У Європі магічні квадрати почали розглядати лише на початку XV ст. Видатний німецький художник і гравер Альбрехт Дюрер, який цікавився і математикою теж, увічнив магічний квадрат у найкращій своїй гравюрі «Меланхолія» (1514). Два середніх числа в останньому рядку складають рік створення гравюри. Цей квадрат називають квадратом Дюрера, його можна отримати з основного квадрата, виконавши поворот на 180°.

Незважаючи на таку давню історію, теорія магічних квадратів ще далека до завершення. Зокрема ще не знайдено відповіді на запитання — скільки різних заповнень має квадрат четвертого порядку натуральними числами від 1 до 16 (порядок квадрата визначається числом відрізків, на яке поділено його сторону)?

Властивості основного магічного квадрата 4 x 4

1. Сума чисел, розміщених у куточках цього квадрата, дорівнює магічній константі (рис. 35).

2. Сума чисел у кожному з малих квадратів (2 х 2), що дотикаються до вершин даного квадрата, і у центральному квадраті також однакові та кожна з них дорівнює магічній константі 34 (рис. 36,37).

3. У кожному рядку є пара чисел, які стоять поряд і сума яких дорівнює

15, і ще є пара чисел, які також стоять поряд і сума яких дорівнює 19 (рис. 38).

4. У кожному стовпчику є пара чисел, які стоять поряд і сума яких дорівнює 13, і ще є пара чисел, які також стоять поряд і сума яких — 21 (рис. 39).

5. Магічній константі квадрата дорівнює сума чисел на протилежних сторонах двох центральних прямокутників 2 x 4 (рис. 40).

6. Суми квадратів чисел у двох крайніх рядках рівні між собою:

1²+14² +15² +4² = ІЗ² + 2² + 3² +16² = 438.

Суми квадратів чисел у двох середніх рядках рівні між собою:

12² + 7²+6²+ 9² = 8² + 11²+ 10² + 5²=310.

7. Суми квадратів чисел двох крайніх стовпчиків рівні між собою. Суми

квадратів двох середніх стовпчиків також рівні між собою:;

1² + 12² + 8² + 13² = 4 ² + 9² + 5² + 16² = 378;

14² + 7² + 11² + 2² = 15² + 6² + 10² + 3².

8. Якщо в даний квадрат вписати ще один квадрат, вершинами якого є середини сторін даного квадрата (рис. 41 на с. 54), то:

1) сума чисел, які розміщені вздовж однієї пари протилежних сторін вписаного квадрата, дорівнює сумі чисел, розміщених уздовж іншої пари протилежних сторін, і кожна з цих сум дорівнює 34:

12+14 + 3 + 5 = 15 + 9 + 8 + 2 = 34;

2) рівними між собою є також квадрати і суми кубів цих чисел:

12² + 14² + 3² + 5² = 15² + 9² + 8² + 2² = 374;

12³ + 14³ + 3³ + 5³ = 15³ + 9³ + 8³ + 2³ = 4624.

9. Магічній константі квадрата дорівнює сума чисел у клітинках, позначених ходом шахового коня (рис, 42,43).

1 + 6 + 16 + 11 = 1 + 11 + 16 + 6 = 34; 14 + 9 + 3 + 8 = 34; 15 + 5 + 2 + 12 = 34.

Можливі інші варіанти.

10. Магічній константі квадрата дорівнює сума чисел у клітинках, позначених «довгим» ходом шахового коня (рис. 44).

1+9 + 8 + 16 = 34; 4 + 3 + 14+13 = 34;

1+2+15 + 6 = 34; 4+1 2 + 5 + 13 = 34.

11. Магічній константі квадрата дорівнює сума чисел відповідних діагоналей малих квадратів (2 х 2), що прилягають до протилежних вершин (рис. 45).

12+14+3+5 = 34 і зрозуміло, 1+7+10+16 = 34.

12. Будь-які два числа, розміщені симетрично відносно центра квадрата,

в сумі дорівнюють числу 17 (у загальному випадку, якщо квадрат порядку п, то сума дорівнює 1 + п2) (рис. 46).

12 + 5= 14 + 3 = 11 + 6 = 13+4 = 8 + 9 = . . . = 17.

Розглянуті властивості не вичерпують повністю властивостей магічного

квадрата.

Так, якщо всі стовпчики магічного квадрата переробити на рядки, зберігаючи їхнє чергування, тобто числа першого стовпчика у тій самій послідовності розмістити у вигляді першого рядка, числа другого стовпчика – другого рядка і т. д., то отримаємо квадрат з такими самими властивостями.

Проте інколи під час перестановки окремих рядків чи стовпчиків деякі з властивостей магічного квадрата можуть зникнути. Наприклад, після перестановки першого та другого стовпчиків суми в рядках і стовпчиках залишаються тими самими, а суми чисел, розташованих на діагоналях, змінюються. В такому випадку магічний квадрат втрачає частину своїх властивостей і його називають напівмагічним.

На думку дослідників літературної спадщини Йоганна Вольфганга Ґете, відома сцена приготування відьмою омолоджувального зілля для Фауста є описом перетворення звичайного квадрата, у якого в 9 клітинках розміщені у порядку зростання перші дев’ять натуральних чисел, у квадрат, де суми чисел у рядках і стовпчиках дорівнюють 15.

Du must verstehen! Aus Eins mach ’Zehn

Und Zwei lass gehn

Und Drei mach 'gleich

So bist reich.

Verlier die Vier!

Aus Funf und Sechs,

So sagt die Hex,

Mach’ Sieben und Acht,

So its 's vollbracht;

Und Neun its Eins,

Und Zehn its keins,

Das its das Hexen - Einmal - Eins!

Із одиниці робиш 10,

пропускаєш 2

і також 3.

Закреслюєш 4.

Із 5 і б

робиш 7 і 8 (і навпаки).

Квадрат уже готовий.

Із перестановками рядків і стовпців квадрата пов’язано багато цікавих завдань, які можна запропонувати учням. Наприклад, змінивши місцями рядки і стовпчики основного магічного квадрата 4x4, отримати новий квадрат, у якого: 1) виконувалися б основні властивості магічного квадрата (були рівними суми вздовж кожного рядка, стовпця і діагоналі); 2) суми квадратів чисел уздовж діагоналей були однакові; 3) суми кубів чисел уздовж діагоналей були однакові.

Зрозуміло, що ці завдання слід пропонувати учням, які вже добре засвоїли «ази» побудов і перетворень магічних квадратів.

Розпочинати практичне знайомство з магічними квадратами слід із нескладних завдань для квадратів третього порядку.

Умовно завдання, пов’язані з магічними квадратами, можна поділити на такі види: а) побудова квадрата заданого порядку п із заповненням його послідовними натуральними числами 1, 2, ... п²; б) заповнення квадратів числами, які не повторюються, якщо у деяких клітинках квадрата вже стоять

певні (задані) числа; б) заповнення квадратів, у яких всі клітинки порожні, і відомо лише набір чисел (не обов’язково послідовних), які потрібно розмістити у цих клітинках, а сума чисел у рядках, стовпцях і діагоналях невідома (тобто невідома магічна константа); в) магічна константа відома і відомий набір чисел (числа можуть повторюватися).

Наведемо різні види завдань, які можна розв’язувати з учнями на заняттях

гуртка чи пропонувати їм на конкурсах.

Задачі на побудову магічних квадратів п-го порядку (заповнення квадратів розмірами пхп «натуральними числами від 1 до п2) протягом тисячоліть цікавили як любителів математики, так і вчених-математиків.

Існує багато цікавих способів побудови магічних квадратів непарних і парних порядків. Наведемо приклади їх використання на заняттях математичного гуртка.

Задача 1. Побудуйте магічний квадрат п’ятого порядку так, щоб виконувалися «магічні» властивості,

ОСМ. Нехай потрібно заповнити квадрат АВСD із 25 клітинок.

Крок 1. На кожній зі сторін квадрата добудовуємо фігуру з трьох сходинок (рис. 47).

Крок 2. У цій фігурі, починаючи з верхньої сходинки, навскіс зліва направо розставляємо числа 1, 2, ...,25 (рис. 48). Числа, які опинилися в середині квадрата АВСD, уже стоять на своїх місцях.

Крок 3. Кожне з чисел, які опинилися зовні квадрата, потрібно перемістити вздовж того самого рядка чи стовпчика, в якому вони стоять, на 5 клітинок. Якщо числа стоять над квадратом, то опускаємо їх униз відповідними стовпчиками: число 6 розміщуємо між числами 23 і 19, число 1 над числом 19, а число 2 – між числами 19 і 15. Аналогічно для чисел, які стоять зліва від квадрата АВСD: число 16 треба розмістити між числами 3 і 9, число 21- у тому самому рядку між числами 3 і 9 і т. д.

Після того як усі числа опиняться у середині квадрата АВСD, отримаємо магічний квадрат 5-го порядку (рис. 49).

Безпосередньою перевіркою можна переконатися, що суми чисел уздовж кожного рядка, кожного стовпця і кожної діагоналі однакові і дорівнюють 65.

Крім того, утворений квадрат має властивість, яка відсутня у квадрата 4-го порядку: усі пари чисел, які розміщені симетрично відносно центральної клітинки (числа 13), утворюють однакові суми. Наприклад,

12+ 14=25 + 1 = 8 + 18 = 21 + 5= 16+ 10 = 3 + 23 = 9+ 17 т . д.

Магічні квадрати з такими властивостями іноді називають симетричними.

Зауважимо, що описаний вище спосіб побудови магічного квадрата 5-го порядку можна використати для побудови квадратів будь-якого непарного порядку. Тому можна давати завдання учням будувати квадрати 3-го, 7-го чи 9-го порядку за наведеним зразком з наступним знаходженням відповідних магічних констант та перевірки наявності основних властивостей магічних квадратів.

Задача 2. Побудуйте квадрат 4-го чи 8-го порядку (правило побудови квадратів порядку п = 4k).

ОСМ. Крок 1. У клітинках квадрата 4 x 4 (або 8 x 8 ) розміщуємо зліва направо числа в порядку зростання.

Крок 2. Виділяємо у кутах даного квадрата чотири квадрати зі сторонами та один квадрат у центрі зі стороною (рис. 50).

Крок 3. У кожному з п’яти отриманих квадратів міняємо місцями числа, розміщені симетрично відносно центра даного початкового квадрата. Тобто міняємо місцями числа 1 і 16,13 і 4,6 і 11,7 і 10. Отримали магічний квадрат 4-го порядку (рис. 51).

Крок 3 можна зробити інакше. Залишити на місцях числа у п’яти виділених квадратах, а обмін зробити між числами 4-х прямокутників: тобто поміняти місцями 2 і 15,3 і 14, 5 і 12,9 і 8. Отримаємо новий магічний квадрат

4-го порядку (рис. 52).

Задача 3. Побудуйте квадрат парного порядку за умови, що п = 6.

Для побудови квадрата 6-го порядку використаємо правило рамки:

1) довільним способом будується магічний квадрат порядку п – 2 (тобто порядок допоміжного квадрата кратний 4);

2) утворений квадрат вставляється в рамку, разом з якою утворює магічний квадрат порядку п.

За принципом своєї побудови цей спосіб дає можливість добудовувати магічні квадрати 4-го, 8-го порядку до магічних квадратів 6-го, 10-го порядків і т. д.

Описаний метод можна також використовувати для побудови магічних квадратів непарних порядків.

Розглянемо більш детально кроки побудови квадрата 6-го порядку.

Крок 1. Складаємо довільний магічний квадрат 4-го порядку (рис. 53)

Крок 2. Кожне число цього квадрата збільшуємо на 10 (загальна формула для обчислення числа, на яке потрібно збільшувати, 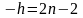). Отримаємо новий квадрат (рис. 54).

Крок 3. Отриманий квадрат доповнимо рамкою в 1 клітинку. Клітинки рамки заповнюємо числами 1, 2, ..., 10 (у загальному випадку — 1, 2, ..., 2п–2) і числами 27, 28, ..., 36 (у загальному випадку — від до п² включно).

Заповнити рамку можна після кількох спроб, попередньо обчисливши магічну константу за формулою:

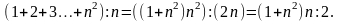
Також допомагає в заповненні рамки використання властивостей магічних квадратів.

Магічне число квадрата на рис. 54 дорівнює 74, а магічне число квадрата 6-го порядку — 111 (111 – 74 = 37). Тому, якщо деяке з чисел 1,2,..., 10 розміщуємо у лівому (правому) верхньому куточку рамки, то його доповнення до 37 у нижньому правому (лівому) куточку, тобто по діагоналі. Якщо деяке із чисел 1,2, ..., 10 розміщуємо вгорі рамки, то у тому самому стовпчику у нижній частині рамки розміщуємо його відповідне доповнення із чисел 27,28, . ..,36 (рис. 55, 56).

Так із квадрата 4-го порядку отримуємо квадрат 6-го порядку (рис. 57).

Наведені вище міркування щодо побудови магічних квадратів різних порядків та перелік їх основних властивостей можна використати як для учнівських доповідей, так і для складання різного виду практичних завдань.

Задача 4. Доведіть, що сума всіх чисел будь-якого магічного квадрата 3x3 буде ділитися на 3.

Розв’язання. Нехай маємо квадрат, який заповнили необов’язково послідовними числами (рис. 58).

Знайдемо суми чисел, що стоять у першому, другому і третьому рядках відповідно. Кожна з цих сум дорівнює магічній константі К. Отже, (а+б+в)+(г+д + е) + (ж + з + и) = К +К +К = 3К.