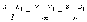30) Условие параллельности и перпендикулярности прямой и плоскости. Условие принадлежности прямой и плоскости.

Условия параллельности и перпендикулярности прямой и плоскости

 

Пусть прямая задана каноническими уравнениями 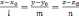 , а плоскость общим уравнением  .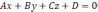

Прямая и плоскость параллельны тогда и только тогда, когда направляющий вектор прямой   и нормальный вектор плоскости   перпендикулярны, то есть их скалярное произведение равно нулю 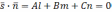  – условие параллельности прямой и плоскости

Прямая и плоскость перпендикулярны тогда и только тогда, когда направляющий вектор прямой   и нормальный вектор   плоскости коллинеарны  – условие перпендикулярности прямой и плоскости.

Условие принадлежности прямой к плоскости
Прямая:  Плоскость: A X + B Y + C Z + D = 0 Очевидно, что координаты точки x1 y1 z1 должны удовлетворять уравнению плоскости: A X1 + B Y1 + C Z1 + D = 0 И условие параллельности прямой и плоскости должно выполняться: A L + B M + C N = 0 Эти два условия определяют принадлежность прямой к плоскости.

31) Эллипс и его свойства.

Эллипс - геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний до двух данных точек   и    = 2c (называемыхфокусами) постоянна и больше расстояния между фокусами, то есть

 причем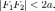 

F1F2=2c

По определению эллипса 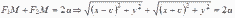. Преобразуем это уравнение:

Разделим обе части этого уравнения на получим:

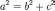=> => - Каноническое уравнение

e=   называется эксцентриситетом.

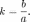коэффициент сжатия эллипса

X= или - Директриса

F1F2=2c – расстояние между фокусами.

D= a - ex

D1=a + ex – фокальные радиусы

32) Гипербола и ее свойства.

 Это уравнение называется каноническим уравнением гиперболы.

Свойство 1

Гипербола имеет две взаимно перпендикулярные оси симметрии.

Свойство 2

Гипербола имеет центр симметрии..

Центр симметрии гиперболы называют центром гиперболы .

Прямые с уравнениями    и    называются асимптотами гиперболы.

.

.

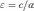F1F2=2c – расстояние между фокусами.

         . Фокальный параметр .

X= - Директриса

33) Парабола и ее свойства.

Парабола — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).

Каноническое уравнение параболы в прямоугольной системе координат:

 (или 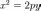 , если поменять местами оси).

Уравнение директрисы  :  , фокус —  , таким образом начало координат   — середина отрезка  . По определению параболы для любой точки  , лежащей на ней выполняется равенство 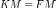 .   и  , тогда равенство приобретает вид:

.

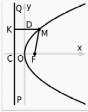
После возведения в квадрат и некоторых преобразований получается равносильное уравнение  .

Число p называется фокальным параметром, оно равно расстоянию от фокуса до директрисы

Директриса и фокус имеют координаты (-p/2 и p/2).

Эллипс симметричен относительно осей координат

Эллипс имеет точки пересечения с осями координат: .

Эллипс содержится в прямоугольнике: .

D1=D2=x+p/2