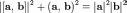16) Векторное произведение двух векторов: геометрические и алгебраические свойства векторного произведения.

Три некомпланарных (не лежащих в одной плоскости) вектора a, b и c взятые в указанном порядке, образуют правую тройку, если с конца вектора c кратчайший поворот от вектора a к вектору b виден совершающимся против часовой стрелки, и левую, если по часовой.

Вектор   называется векторным произведением неколлинеарных векторов   и  , если:

1) его длина равна произведению длин векторов   и   на синус угла между ними: 

2) вектор   ортогонален векторам   и  ;

3) векторы  ,  ,   (в указанном порядке) образуют правую тройку.

Векторное произведение коллинеарных векторов (в частности, если хотя бы один из множителей — нулевой вектор) считается равным нулевому вектору.

Векторное произведение обозначается   (или  ).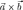

Алгебраические свойства векторного произведения

  ;

 ;

  .

Геометрические свойства векторного произведения

Необходимым и достаточным условием коллинеарности двух ненулевых векторов является равенство нулю их векторного произведения.

Модуль векторного произведения   равняется площади   параллелограмма, построенного на приведённых к общему началу векторах   и   

Если   — единичный вектор, ортогональный векторам   и   и выбранный так, что тройка 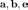  — правая, а   — площадь параллелограмма, построенного на них (приведённых к общему началу), то для векторного произведения справедлива формула:

Если   — какой-нибудь вектор,   — любая плоскость, содержащая этот вектор,   — единичный вектор, лежащий в плоскости   и ортогональный к  ,   — единичный вектор, ортогональный к плоскости   и направленный так, что тройка векторов   является правой, то для любого лежащего в плоскости   вектора   справедлива формула

17) Векторное произведение двух векторов: выражение векторного произведения в декартовой системе координат.

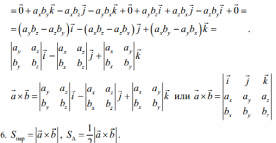
18) Смешанное произведение векторов и его свойства.

19) Смешанное произведение в декартовой системе координат.

20) Общее уравнение прямой. Неполное уравнение прямой, уравнение прямой в отрезках.

Уравнение вида формула есть общее уравнение прямой на плоскости в прямоугольной системе координат Oxy. Из доказательства теоремы также видно, что коэффициенты А и В при переменных x и y являются соответствующими координатами нормального вектора прямой, заданной общим уравнением прямой вида.

Если один или два из трех коэффициентов (считая и свободный член) обращаются в нуль, то уравнение называется неполным. Возможны следующие случаи:

1). С=0; уравнение имеет вид 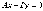  и определяет прямую, проходящую через начало координат.

2). В=0 (А0); уравнение имеет вид 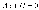  и определяет прямую, перпендикулярную к оси Ох. Это уравнение может быть записано в виде х=а, где  является величиной отрезка, который отсекает прямая на оси Ох, считая от начала координат.

3). В=0, С=0 (А0); уравнение может быть записано в виде х=0 и определяет ось ординат.

4). А=0 (В0); уравнение имеет вид   и определяет прямую, перпендикулярную к оси Оу. Это уравнение может быть записано в виде y=b, где 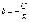 является величиной отрезка, который отсекает прямая на оси Оу, считая от начала координат.

5). А=0, С=0 (В0); уравнение может быть записано в виде у=0 и определяет ось абсцисс.

Если ни один из коэффициентов уравнения (1) не равен нулю, то его можно преобразовать к виду

, (2)

где  ,   суть величины отрезков, которые отсекает прямая на координатных осях.

Уравнение (2) называется уравнением прямой «в отрезках».

Если две прямые даны уравнениями

 и  ,

то могут представиться три случая:

а).   - прямые имеют одну общую точку;

б). 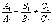  - прямые параллельны;

в).   - прямые сливаются, то есть оба уравнения определяют одну и ту же прямую.