1)

А) Свойства определителей второго порядка:

1.При умножении элементов любого столбца определителя на число α, его величина умножается на это же число.

 2.При перестановке строк определитель изменяет знак на противоположный.

3.Если один из столбцов определителя равен нулю, то и определитель равен нулю.

4. Определитель с одинаковыми строками равен нулю.

5.Определитель с пропорциональными строками равен нулю

6.Определитель диагональной матрицы равен произведению ее диагональных элементов

7.Определитель треугольной матрицы равен произведению ее диагональных элементов.

8.Если в определителе строки поменять местами со столбцами, то определитель не изменится.

Б) Решение систем уравнений второго порядка:

Шаг 1 Сосчитать главный определитель системы D

Шаг 2 Сосчитать Dx и Dy по формулам:

Dx = 

Dy = 

Шаг 3 Сосчитать x = Dx/D 8 y = Dy/D:

2)Определители третьего порядка и их свойства:

Свойство 1. Если все элементы какой-либо строки (столбца) определителя 3-го порядка равны нулю, то и определитель равен нулю. 

Свойство 2. Определитель 3-го порядка не изменится, если его строки заменить столбцами с теми же номерами. 

Свойство 3. Если поменять местами две строки (столбца) определителя 3-го порядка, то обсолютная величина определителя не изменится, а знак изменится на противоположный. 

Следствие. Определитель 3-го порядка, в котором каких-либо две строки (столбца) совпадают, равен нулю.

Свойство 4. Если все элементы какой-либо строки (столбца) определителя 3-го порядка умножить на какое-либо число, то и определитель умножится на это число. 

Следствие 1. Если все элементы какой-либо строки (столбца) имеют общий множитель, то этот множитель можно вынести за знак определителя.

Следствие 2. Если все элементы какой-либо строки (столбца) определителя 3-го порядка пропорциональны соответствующим элементам другой строки (столбца) этого определителя, то определитель равен нулю.

3. Алгебраические дополнения и миноры.

(знаю)

4. Обратная матрица.

Обратная матрица — такая матрица A⁻¹, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:

Найдем определитель главной матрицы. Найдем матрицу алгебраических дополнений.

Вспоминаем нашу формулу и решим 

5) Ранг матрицы.

Находим миноры первого порядка, если в матрице есть ненулевые элементы, то её ранг не меньше единицы. Дальше находим минор 3 порядка, 4 и 5. Таким образом, ранг матрицы равен максимальному порядку ненулевого минора.

6) Решение систем уравнений третьего порядка. Правило Крамера.

Система линейных уравнений с вещественными коэффициентами:

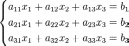
Определители:

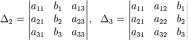
В определителях столбец коэффициентов при соответствующей неизвестной заменяется столбцом свободных членов системы.

Решение:

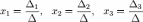
7) Теорема Крамера.

Доказательство. Пусть A - основная матрица системы (4.4), ∆ - ее определитель (главный определитель системы), X - столбец из ее неизвестных и B – столбец свободных членов системы. Тогда уравнение AX = B представляет собой матричную запись системы. Так как по условию теоремы A - невырожденная матрица, то она имеет обратную Умножим обе части равенства

Если в системе   линейных уравнений с   неизвестными 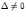  , то система имеет решение и притом единственное. Это решение задается формулами

        Доказательство.  По теореме обратная матрица находится по формуле

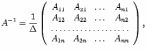
где   -- алгебраические дополнения. Тогда из (15.3) следует, что

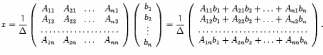
Заметим, что по формуле (14.13) разложение определителя   по первому столбцу в точности совпадает с первым элементом матрицы-столбца в правой части последнего равенства, разложение определителя   по второму столбцу дает второй элемент матрицы-столбца и т.д. Поэтому   , откуда и следует утверждение теоремы.      

8) Неоднородная система трех линейных уравнений с тремя неизвестными с определителем, равным нулю.

Такая система не имеет решений!

9) Однородная система трех линейных уравнений с тремя неизвестными:

Совершенно ясно, что однородная система всегда совместна, то есть всегда имеет решение. И, прежде всего, в глаза бросается так называемое тривиальное решение 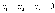 .  Так как каждый из определителей имеет столбец, все члены которого равны нулю.

10) Метод последовательного исключения неизвестных ( Метод Гауса )

(Долго писать)

11) Понятие вектора. Действия с векторами:

Вектором называется направленный отрезок, для которого указано его начало и конец.

 Длиной вектора называется длина этого отрезка. Обозначается:   или  .

Сложение векторов

Для сложения векторов есть два способа.

1. Правило параллелограмма. Чтобы сложить векторы   и  , помещаем начала обоих в одну точку. Достраиваем до параллелограмма и из той же точки проводим диагональ параллелограмма. Это и будет сумма векторов   и  .

2. Второй способ сложения векторов — правило треугольника. Возьмем те же векторы   и  . К концу первого вектора пристроим начало второго. Теперь соединим начало первого и конец второго. Это и есть сумма векторов   и  .

По тому же правилу можно сложить и несколько векторов. Пристраиваем их один за другим, а затем соединяем начало первого с концом последнего.

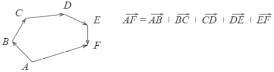
Представьте, что вы идете из пункта А в пункт В, из В в С, из С в D, затем в Е и в F. Конечный результат этих действий — перемещение из А в F.

При сложении векторов   и   получаем:

Вычитание векторов

Вектор   направлен противоположно вектору  . Длины векторов   и   равны.

Теперь понятно, что такое вычитание векторов. Разность векторов   и   — это сумма вектора   и вектора  .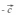

Умножение вектора на число

При умножении вектора   на число k получается вектор, длина которого в k раз отличается от длины  . Он сонаправлен с вектором  , если k больше нуля, и направлен противоположно  , если k меньше нуля.