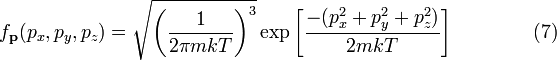26.​ Газ в поле силы тяжести. Барометрическая формула. Распределение Больцмана.

Барометрическая формула:

,

где p — давление газа в слое, расположенном на высоте h, p₀ — давление на нулевом уровне h = h₀, M — молярная масса газа, R — газовая постоянная, T — абсолютная температура.

В присутствии гравитационного поля (или, в общем случае, любого потенциального поля) на молекулы газа действует сила тяжести. В результате, концентрация молекул газа оказывается зависящей от высоты в соответствии с законом распределения Больцмана:

Где: n — концентрация молекул на высоте h, n₀ — концентрация молекул на начальном уровне h = 0, m — масса частиц, g — ускорение свободного падения, k — постоянная Больцмана, T — температура.

В статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, которая находится в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная , а на каждую колебательную степень свободы — в среднем энергия, равная kT. Колебательная степень обладает вдвое большей энергией, т.к. на нее приходится как кинетическая энергия (как в случае поступательного и вращательного движений), так и потенциальная, причем средние значения потенциальной и кинетической и энергии одинаковы. Значит, средняя энергия молекулы:

,

где i — сумма числа поступательных, числа вращательных в удвоенного числа колебательных степеней свободы молекулы: i = i_пост. + i_вращ. + 2i_колеб.

Закон равнораспределения показывает, что при тепловом равновесии, любая степень свободы (компоненты векторов положения или скорость частицы), которая появляется только как квадратичная функция в энергии, обладает средней энергией равной ½k в T и поэтому вносит вклад ½k в теплоёмкость системы.

Газ или жидкость в поле силы тяжести.

Рассмотрим некоторое физтическое тело, состоящее из одного и того же вещества в жидком или газообразном состоянии, занимающее постоянный объем постоянную температуру.

25.​ Распределение Максвелла.

Распределение Ма́ксвелла — распределение вероятности, встречающееся в физике и химии. Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и диффузию. Распределение Максвелла также применимо для электронных процессов переноса и других явлений. Распределение Максвелла применимо к множеству свойств индивидуальных молекул в газе. О нём обычно думают как о распределении энергий молекул в газе, но оно может также применяться к распределению скоростей, импульсов, и модуля импульсов молекул. Также оно может быть выражено как дискретное распределение по множеству дискретных уровней энергии, или как непрерывное распределение по некоторому континууму энергии.

Распределение Максвелла может быть получено при помощи статистической механики (см. происхождение статсуммы). Как распределение энергии, оно соответствует самому вероятному распределению энергии, в столкновительно-доминируемой системе, состоящей из большого количества невзаимодействующих частиц, в которой квантовые эффекты являются незначительными. Так как взаимодействие между молекулами в газе является обычно весьма небольшим, распределение Максвелла даёт довольно хорошее приближение ситуации, существующей в газе.

Во многих других случаях, однако, даже приблизительно не выполнено условие доминирования упругих соударений над всеми другими процессами. Это верно, например, в физике ионосферы и космической плазмы, где процессы рекомбинации и столкновительного возбуждения (то есть излучательные процессы) имеют большое значение, в особенности для электронов. Предположение о применимости распределения Максвелла дало бы в этом случае не только количественно неверные результаты, но даже предотвратило бы правильное понимание физики процессов на качественном уровне. Также, в том случае где квантовая де Бройлева длина волны частиц газа не является малой по сравнению с расстоянием между частицами, будут наблюдаться отклонения от распределения Максвелла из-за квантовых эффектов.

Распределение энергии Максвелла может быть выражено как дискретное распределение энергии:

,

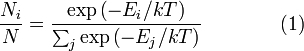где N_i является числом молекул, имеющих энергию E_i при температуре системы T, N является общим числом молекул в системе и k — постоянная Больцмана. (Отметьте, что иногда вышеупомянутое уравнение записывается с множителем g_i, обозначающим степень вырождения энергетических уровней. В этом случае сумма будет по всем энергиям, а не всем состояниям системы). Поскольку скорость связана с энергией, уравнение (1) может использоваться для получения связи между температурой и скоростями молекул в газе. Знаменатель в уравнении (1) известен как каноническая статистическая сумма.

Распределение Максвелла

Распределение по вектору импульса

Представленное ниже очень сильно отличается от вывода, предложенного Джеймсом Клерком Максвеллом и позже описанного с меньшим количеством предположений Людвигом Больцманом.

В случае идеального газа, состоящего из не взаимодействующих атомов в основном состоянии, вся энергия находится в форме кинетической энергии. Кинетическая энергия соотносится с импульсом частицы следующим образом

,

где p² — квадрат вектора импульса p = [p_x, p_y, p_z].

Мы можем поэтому переписать уравнение (1) как:

,

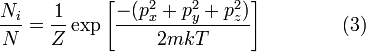где Z — статсумма, соответствующая знаменателю в уравнении (1), m — молекулярная масса газа, T — термодинамическая температура, и k — постоянная Больцмана. Это распределение N_i / N пропорционально функции плотности вероятности f_p нахождения молекулы в состоянии с этими значениями компонентов импульса. Таким образом:

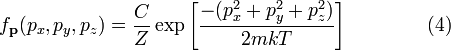
Постоянная нормировки C, определяется из условия, в соответствии с которым вероятность того, что молекулы имеют какой-либо вообще импульс, должна быть равна единице. Поэтому интеграл уравнения (4) по всем значениям p_x, p_y и p_z должен быть равен единице. Можно показать, что:

.

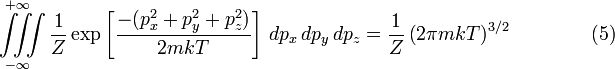Таким образом, чтобы интеграл в уравнении (4) имел значение 1 необходимо, чтобы

.

Подставляя выражение (6) в уравнение (4) и используя тот факт, что p_i = m v_i, мы получим