20. Коэффициент детерминации и коэффициент корреляции, их расчет в модели парной регересии.

Величина r² называется коэффициентом детерминации. Он определяет долю вариации одной из переменных, которая объясняется вариацией другой переменной.

Для устранения недостатка ковариации был введён линейный коэффициент корреляции (или коэффициент корреляции Пирсона), Коэффициент корреляции рассчитывается по формуле^[10][8]:

где , — среднее значение выборок.

Коэффициент корреляции изменяется в пределах от минус единицы до плюс единицы. С помощью множественного коэффициента корреляции характеризуется совокупное влияние всех факторных переменных на результативную переменную в модели множественной регрессии.

Коэффициент множественной корреляции для линейной модели множественной регрессии с n факторными переменными рассчитывается через стандартизированные частные коэффициенты регрессии и парные коэффициенты корреляции по формуле:

где r (yxi) – парный (не частный) коэффициент корреляции между результативной переменной у и факторной переменной xi.

.

где r (yxi) – парный (не частный) коэффициент корреляции между результативной переменной у и факторной переменной xi

21. Средняя относительная ошибка аппроксимации Величина отклонений фактических и расчетных значений результативного признака   по каждому наблюдению представляет собой ошибку аппроксимации.

Поскольку   может быть как величиной положительной, так и отрицательной, то ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.

Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению определяют среднюю ошибку аппроксимации: 

22. Проверка значимости уравнения регрессии в целом. F-критерий Фишера.

Значимость уравнения регрессии, т.е. соответствие эконометрической модели Y = aˆ0 + aˆ 1X + e фактическим (эмпирическим) данным, позволяет ус-

тановить, пригодно ли уравнение регрессии для практического использования (для анализа и прогноза), или нет.

Для проверки значимости уравнения используется F - критерий Фишера. Он вычисляется по фактическим данным как отношение несмещенной

дисперсии остаточной компоненты к дисперсии исходного ряда. Проверка значимости коэффициента детерминации осуществляется с помощью -критерия Фишера, расчетное значение которого находится по формуле:

,

,

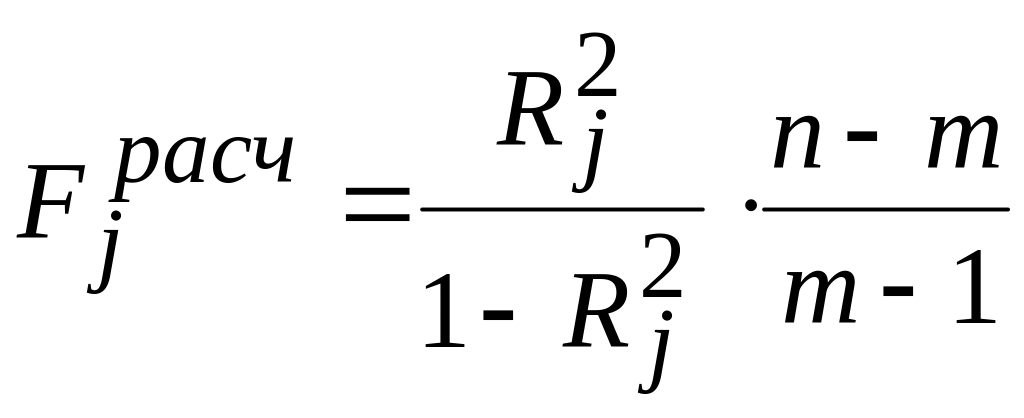где коэффициент множественной корреляции, – количество наблюдений, - количество переменных, – диагональный элемент матрицы .

Для проверки гипотезы по таблице определяют табличное значение

критерия Фишера F .

F( α ν1 ν2) – это максимально возможное значение критерия в зависимости от влияния случайных факторов при данных степенях свободы

ν = m1, ν2 = n − m −1, и уровне значимости α . Здесь m – количество аргументов в модели.

Уровень значимости α – вероятность отвергнуть правильную гипотезу, но при условии, что она верна (ошибка первого рода). Обычно α принимается равной 0,05 или 0,01.

Если Fф> Fтабл , то H0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если наоборт, то гипотеза H0 не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.